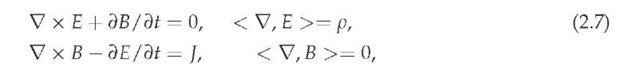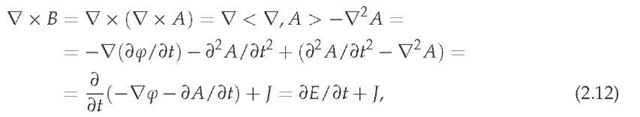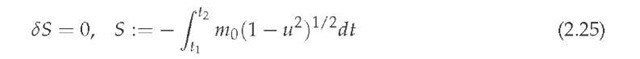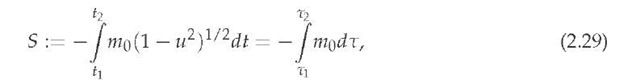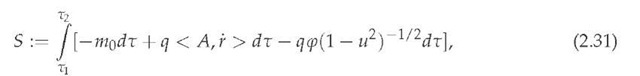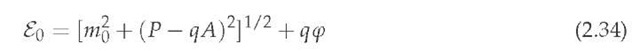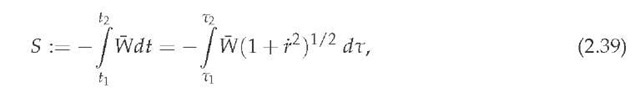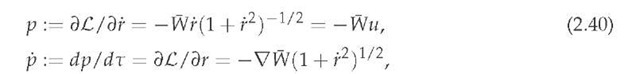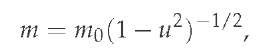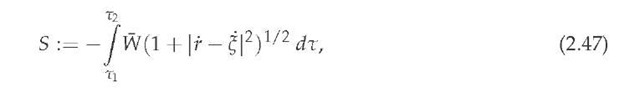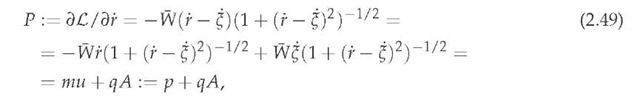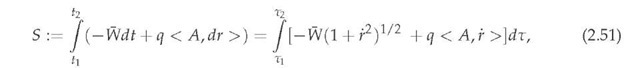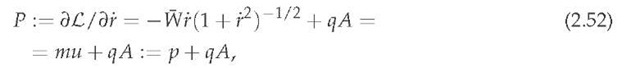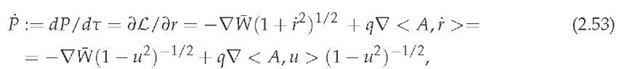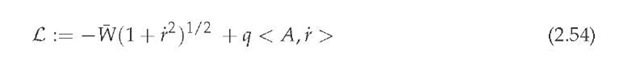Introduction
"A physicist needs his equations should be mathematically sound and that in working with his equations he should not neglect quantities unless they are small" P.A. M. Dirac Classical electrodynamics is nowadays considered [29; 57; 80] the most fundamental physical theory, largely owing to the depth of its theoretical foundations and wealth of experimental verifications. Electrodynamics is essentially characterized by its Lorentz invariance from a theoretical perspective, and this very important property has had a revolutionary influence [29; 57; 80; 102; 111] on the whole development of physics. In spite of the breadth and depth of theoretical understanding of electromagnetism, there remain several fundamental open problems and gaps in comprehension related to the true physical nature of Maxwell’s theory when it comes to describing electromagnetic waves as quantum photons in a vacuum: These start with the difficulties in constructing a successful Lagrangian approach to classical electrodynamics that is free of the Dirac-Fock-Podolsky inconsistency [53; 111; 112], and end with the problem of devising its true quantization theory without such artificial constructions as a Fock space with "indefinite" metrics, the Lorentz condition on "average", and regularized "infinities" [102] of S-matrices. Moreover, there are the related problems of obtaining a complete description of the structure of a vacuum medium carrying the electromagnetic waves and deriving a theoretically and physically valid Lorentz force expression for a moving charged point particle interacting with and external electromagnetic field. To describe the essence of these problems, let us begin with the classical Lorentz force expression
is its velocity vector, expressed here in the
light speed c units, is a particle electric charge,
is its velocity vector, expressed here in the light speed c units,
is the corresponding external electric field and
is the corresponding external magnetic field, acting on the charged particle, expressed in terms of suitable vector A : M4 ^ E3 and scalar p : M4 ^ R potentials. Here "V" is the standard gradient operator with respect to the spatial variable r £ E3, " x " is the usual vector product in three-dimensional Euclidean vector space E3, which is naturally endowed with the classical scalar product < •, • >. These potentials are defined on the Minkowski space M4 := R x E3, which models a chosen laboratory reference system K. Now, it is a well-known fact [56; 57; 70; 80] that the force expression (2.1) does not take into account the dual influence of the charged particle on the electromagnetic field and should be considered valid only if the particle charge q ^ 0. This also means that expression (2.1) cannot be used for studying the interaction between two different moving charged point particles, as was pedagogically demonstrated in [57].
Other questionable inferences, which strongly motivated the analysis in this work, are related both to an alternative interpretation of the well-known Lorentz condition, imposed on the four-vector of electromagnetic potentials (p, A) : M4 ^ R x E3 and the classical Lagrangian formulation [57] of charged particle dynamics under an external electromagnetic field. The Lagrangian approach is strongly dependent on the important Einsteinian notion of the rest reference system Kr and the related least action principle, so before explaining it in more detail, we first analyze the classical Maxwell electromagnetic theory from a strictly dynamical point of view.
Relativistic electrodynamics models revisited: Lagrangian and Hamiltonian analysis
The Maxwell equations revisiting
Let us consider the additional Lorentz condition
imposed a priori on the four-vector of potentials (p, A) : M4 ^ R x E3, which satisfy the Lorentz invariant wave field equations
where p : M4 ^ R and J : M4 ^ E3 are, respectively, the charge and current densities of the ambient matter, which satisfy the charge continuity equation
Then the classical electromagnetic Maxwell field equations [56; 57; 70; 80]
hold for all (t, r) £ M4 with respect to the chosen reference system K.
Notice here that Maxwell’s equations (2.7) do not directly reduce, via definitions (2.2) and (2.3), to the wave field equations (2.5) without the Lorentz condition (2.4). This fact is very important, and suggests that when it comes to a choice of governing equations, it may be reasonable to replace Maxwell’s equations (2.7) and (2.6) with the Lorentz condition (2.4), (2.5) and the continuity equation (2.6). From the assumptions formulated above, one infers the following result.
Proposition 2.1. The Lorentz invariant wave equations (2.5) for the potentials (f, A) : M4 ^ R x E3, together with the Lorentz condition (2.4) and the charge continuity relationship (2.5), are completely equivalent to the Maxwell field equations (2.7).
Proof. Substituting (2.4), into (2.5), one easily obtains
which implies the gradient expression
Taking into account the electric field definition (2.2), expression (2.9) reduces to
which is the second of the first pair of Maxwell’s equations (2.7).
Now upon applying Vx to definition (2.2), we find, owing to definition (2.3), that
which is the first of the first pair of the Maxwell equations (2.7). Applying Vx to the definition (2.3), one obtains
leading to
which is the first of the second pair of the Maxwell equations (2.7). The final "no magnetic charge" equation
in (2.7) follows directly from the elementary identity
thereby completing the proof.
This proposition allows us to consider the potential functions
fundamental ingredients of the ambient vacuum field medium, by means of which we can try to describe the related physical behavior of charged point particles imbedded in space-time M4. The following observation provides strong support for this approach:
Observation. The Lorentz condition (2.4) actually means that the scalar potential field p : M4 R continuity relationship, whose origin lies in some new field conservation law, characterizes the deep intrinsic structure of the vacuum field medium.
To make this observation more transparent and precise, let us recall the definition [56; 57; 70; 80] of the electric current J : M4 ^ E3 in the dynamical form
where the vector v : M4 ^ E3 is the corresponding charge velocity. Thus, the following continuity relationship
holds, which can easily be recast [122] as the integral conservation law
moving in the space-time M4 with for the charge inside of any bounded domain
moving in the space-time M4 with respect to the natural evolution equation
Following the above reasoning, we are led to the following result.
Proposition 2.2. The Lorentz condition (2.4) is equivalent to the integral conservation law
where
is any bounded domain moving with respect to the evolution equation
which represents the velocity vector of local potential field changes propagating in the Minkowski space-time M4.
Proof. Consider first the corresponding solutions to the potential field equations (2.5), taking into account condition (2.13). Owing to the results from [57; 70], one finds that
which gives rise to the following form of the Lorentz condition (2.4):
This obviously can be rewritten [122] as the integral conservation law (2.17), so the proof is complete. □
The above proposition suggests a physically motivated interpretation of electrodynamic phenomena in terms of what should naturally be called the vacuum potential field, which determines the observable interactions between charged point particles. More precisely, we can a priori endow the ambient vacuum medium with a scalar potential field function
satisfying the governing vacuum field equations
taking into account that there are no external sources besides material particles possessing only a virtual capability for disturbing the vacuum field medium. Moreover, this vacuum potential field function W : M4 ^ R allows the natural potential energy interpretation, whose origin should be assigned not only to the charged interacting medium, but also to any other medium possessing interaction capabilities, including for instance, material particles interacting through the gravity.
This leads naturally to the next important step, which consists in deriving the equation governing the corresponding potential field W : M4 ^ R, assigned to the vacuum field medium in a neighborhood of any spatial point moving with velocity u £ E3 and located at R(t) £ E3 at time t £ R. As can be readily shown [53; 54], the corresponding evolution equation governing the related potential field function W : M4 ^ R has the form
at point particle location
at point particle location
Similarly, if there are two interacting point particles, located at points R(t) and Rf (t) £ E3 at time t £ R and moving, respectively, with velocities u := dR(t) /dt and uf := dRf (t)/dt, the corresponding potential field function W : M4 ^ R for the particle located at point R(t) £ E3 should satisfy
The dynamical potential field equations (2.22) and (2.23) appear to have important properties and can be used as a means for representing classical electrodynamics. Consequently, we shall proceed to investigate their physical properties in more detail and compare them with classical results for Lorentz type forces arising in the electrodynamics of moving charged point particles in an external electromagnetic field.
In this investigation, we were strongly inspired by the works [81; 82; 89; 91; 93]; especially by the interesting studies [87; 88] devoted to solving the classical problem of reconciling gravitational and electrodynamical charges within the Mach-Einstein ether paradigm. First, we revisit the classical Mach-Einstein relativistic electrodynamics of a moving charged point particle, and second, we study the resulting electrodynamic theories associated with our vacuum potential field dynamical equations (2.22) and (2.23), making use of the fundamental Lagrangian and Hamiltonian formalisms which were specially devised for this in [52; 55]. The results obtained are used to apply the canonical Dirac quantization procedure to the corresponding energy conservation laws associated to the electrodynamic models considered.
Classical relativistic electrodynamics revisited
The classical relativistic electrodynamics of a freely moving charged point particle in the Minkowski space-time M4 := R x E3 is based on the Lagrangian approach [56; 57; 70; 80] with Lagrangian function
where m0 £ R+ is the so-called particle rest mass and u £ E3 is its spatial velocity in the Euclidean space E3, expressed here and in the sequel in light speed units (with light speed c). The least action principle in the form
gives rise to the well-known relativistic for any fixed temporal interval
gives rise to the well-known relativistic relationships for the mass of the particle
the momentum of the particle
and the energy of the particle
It follows from [57; 80], that the origin of the Lagrangian (2.24) can be extracted from the action
on the suitable temporal interval [T1,T2] C R, where, by definitior
and t £ R is the so-called proper temporal parameter assigned to a freely moving particle with respect to the rest reference system Kr. The action (2.29) is rather questionable from the dynamical point of view, since it is physically defined with respect to the rest reference system Kr, giving rise to the constant action S = -ma (T2 — t), as the limits of integrations T1 < T2 £ R were taken to be fixed from the very beginning. Moreover, considering this particle to have charge q £ R and be moving in the Minkowski space-time M4 under action of an electromagnetic field ( p, A) £ R x E3, the corresponding classical (relativistic) action functional is chosen (see [52; 55-57; 70; 80]) as follows:
with respect to the rest reference system, parameterized by the Euclidean space-time variables (t, r) £ E4, where we have denoted r := dr/dT in contrast to the definition u := dr/dt. The action (2.31) can be rewritten with respect to the laboratory reference system K moving with velocity vector ![]()
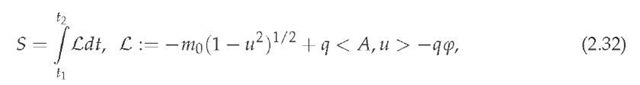
which gives rise to the following [56; 57; 70; 80] on the temporal interval
which gives rise to the following [56; 57; 70; 80] dynamical expressions
for the particle momentum and
for the particle energy, where, by definition, P £ E3 is the common momentum of the particle and the ambient electromagnetic field at a space-time point (t, r) £ M4.
The expression (2.34) for the particle energy £0 also appears open to question, since the potential energy q p, entering additively, has no affect on the particle mass m = m0 (1 — u2)-1/2. This was noticed by L. Brillouin [59], who remarked that since the potential energy has no affect on the particle mass, this tells us that "… any possibility of existence of a particle mass related with an external potential energy, is completely excluded". Moreover, it is necessary to stress here that the least action principle (2.32), formulated with respect to the laboratory reference system K time parameter t £ R, appears logically inadequate, for there is a strong physical inconsistency with other time parameters of the Lorentz equivalent reference systems. This was first mentioned by R. Feynman in [29], in his efforts to rewrite the Lorentz force expression with respect to the rest reference system Kr. This and other special relativity theory and electrodynamics problems induced many prominent physicists of the past [29; 59; 61; 64; 80] and present [4; 5; 60; 65; 66; 68; 69; 81; 82; 87; 89; 90; 93] to try to develop alternative relativity theories based on completely different space-time and matter structure principles.
There also is another controversial inference from the action expression (2.32). As one can easily show [56; 57; 70; 80], the corresponding dynamical equation for the Lorentz force is given as
We have defined here, as before,
for the corresponding electric field and
for the related magnetic field, acting on the charged point particle q. The expression (2.35) means, in particular, that the Lorentz force F depends linearly on the particle velocity vector u £ E3, and so there is a strong dependence on the reference system with respect to which the charged particle q moves. Attempts to reconcile this and some related controversies [29; 59; 60; 63] forced Einstein to devise his special relativity theory and proceed further to creating his general relativity theory trying to explain gravity by means of geometrization of space-time and matter in the Universe. Here we must mention that the classical Lagrangian function L in (2.32) is written in terms of a combination of terms expressed by means of both the Euclidean rest reference system variables (t, r) £ E4 and arbitrarily chosen Minkowski reference system variables (t, r) £ M4.
These problems were recently analyzed using a completely different "no-geometry" approach [6; 53; 54; 60], where new dynamical equations were derived, which were free of the controversial elements mentioned above. Moreover, this approach avoided the introduction of the well-known Lorentz transformations of the space-time reference systems with respect to which the action functional (2.32) is invariant. From this point of view, there are interesting conclusions in [83] in which Galilean invariant Lagrangians possessing intrinsic Poincare-Lorentz symmetry are reanalyzed. Next, we revisit the results obtained in [53; 54] from the classical Lagrangian and Hamiltonian formalisms [52] in order to shed new light on the physical underpinnings of the vacuum field theory approach to the investigation of combined electromagnetic and gravitational effects.
The vacuum field theory electrodynamics equations: Lagrangian analysis
A point particle moving in a vacuum – an alternative electrodynamic model
In the vacuum field theory approach to combining electromagnetism and the gravity devised in [53; 54], the main vacuum potential field function W : M4 ^ R related to a charged point particle q satisfies the dynamical equation (2.21), namely
in the case when the external charged particles are at rest, where, as above, u : = dr/ dt is the particle velocity with respect to some reference system.
To analyze the dynamical equation (2.38) from the Lagrangian point of view, we write the corresponding action functional as
expressed with respect to the rest reference system Kr. Fixing the proper temporal parameters
one finds from the least action principle ![]() that
that
where, owing to (2.39), the corresponding Lagrangian function is
Recalling now the definition of the particle mass
and the relationships
from (2.40) we easily obtain the dynamical equation (2.38). Moreover, one now readily finds that the dynamical mass, defined by means of expression (2.42), is given as
which coincides with the equation (2.26) of the preceding section. Now one can formulate the following proposition using the above results
Proposition 2.3. The alternative freely moving point particle electrodynamic model (2.38) allows the least action formulation (2.39) with respect to the "rest" reference system variables, where the Lagrangian function is given by expression (2.41). Its electrodynamics is completely equivalent to that of a classical relativisticfreely moving point particle, described in Section 2.
An interacting two charge system moving in a vacuum – an alternative electrodynamic model
We proceed now to the case when our charged point particle q moves in the space-time with velocity vector u E3 and interacts with another external charged point particle, moving with velocity vector uf £ E3 in a common reference system K. As shown in [53; 54], the corresponding dynamical equation for the vacuum potential field function W : M4 ^ R is given as
As the external charged particle moves in the space-time, it generates the related magnetic field B := Vx A, whose magnetic vector potential A : M4^ E3 is defined, owing to the results of [53; 54; 60], as
Whence, it follows from (2.40) that the particle momentum ![]() equation (2.44) is equivalent to
equation (2.44) is equivalent to
To represent the dynamical equation (2.46) in the classical Lagrangian formalism, we start from the following action functional, which naturally generalizes the functional (2.39):
which takes into account the relative velocity
which takes into account the relative velocity of the charged point particle q with respect to the reference system K’, moving with velocity ![]() in the reference system K. It is clear in this case that the charged point particle q moves with velocity
in the reference system K. It is clear in this case that the charged point particle q moves with velocity ![]() with respect to the reference system K’ in which the external charged particle is at rest.
with respect to the reference system K’ in which the external charged particle is at rest.
Now we compute the least action variational condition SS = 0 taking into account that, owing to (2.47), the corresponding Lagrangian function is given as
Hence, the common momentum of the particles is
and the dynamical equation is given as
we obtain finally
from (2.50) the dynamical equation (2.46), which leads to the next proposition.
Proposition 2.4. The alternative classical relativistic electrodynamic model (2.44) allows the least action formulation (2.47) with respect to the "rest" reference system variables, where the Lagrangian function is given by expression (2.48).
A moving charged point particle formulation dual to the classical alternative electrodynamic model
It is easy to see that the action functional (2.47) is written utilizing the classical Galilean transformations of reference systems. If we now consider the action functional (2.39) for a charged point particle moving with respect the reference system Kr, and take into account its interaction with an external magnetic field generated by the vector potential A : M4 ^ E3, it can be naturally generalized as
Thus, the corresponding common particle-field momentum takes the form
and satisfies
where
is the corresponding Lagrangian function. Since
one easily finds from (2.53) that
Upon substituting (2.52) into (2.55) and making use of the well-known [57] identity
are arbitrary vector functions, we obtain the classical expression for the
are arbitrary vector functions, we obtain the classical expression for the
Lorentz force F acting on the moving charged point particle q :
where, by definition,
is its associated electric field and
is the corresponding magnetic field. This result can be summarized as follows:
Proposition 2.5. The classical relativistic Lorentz force (2.57) allows the least action formulation (2.51) with respect to the rest reference system variables, where the Lagrangian function is given by formula (2.54). Its electrodynamics described by the Lorentz force (2.57) is completely equivalent to the classical relativistic moving point particle electrodynamics characterized by the Lorentz force (2.35) in Section 2.
As for the dynamical equation (2.50), it is easy to see that it is equivalent to
which, owing to (2.55) and (2.57), takes the following Lorentz type force form
that can be found in [53; 54; 60].
Expressions (2.57) and (2.61) are equal to up to the gradient term
which reconciles the Lorentz forces acting on a charged moving particle q with respect to different reference systems. This fact is important for our vacuum field theory approach since it uses no special geometry and makes it possible to analyze both electromagnetic and gravitational fields simultaneously by employing the new definition of the dynamical mass by means of expression (2.42).