Gouy Phase and Matter Waves (Electromagnetic Waves) Part 3

Atom focalization by classical fields

The interaction between a two-level atom and a single mode of the electromagnetic field (EMF) is governed by the semiclassical hamiltonian

is the dipole moment operator, where £d is the unitary vector along the direction of quantization, p is the element of the transition matrix between the levels e (excited) and g (ground state), and

Assuming the longwave approximation, the electric field E is considered in the position r of the atomic center of mass (r is the corresponding quantum operator). Here, E is treated classically.

Let us suppose that the atom interacts with a stationary electromagnetic wave kept in a cavity. Moreover, the atom moves along the Oz direction, while the stationary field is formed by two counterpropagating components along the Ox axis and linearly polarized in the direction Oy. We have

where E0 is a complex amplitude. Thus, we can write

Here,

where A is the wavelength of the EMF, and h.c. stands for hermitean conjugate.

Without loss of generality, we can take E0 real. Hence,

Assuming

we have

is the Rabi vacuum frequency.

The hamiltonian that governs the atomic dynamics during the interaction with the stationary field is given by

and m is the atomic mass. In the rotating wave approximation

Here,

(RWA), we have and m is the atomic mass. In the rotating wave approximation

In order to remove the temporal dependence of H, we define

Then, the evolution of the state is governed by the equation

where

Here, we define

as the detuning between the frequency of the atomic transition and the frequency of the field mode. In the limit of thin lens, the kinetic energy term can be neglected. So, we have

is an eigenstate of the operator x with eigenvalue x.

Let us define the operator

Consider the set composed by the states

  is an eigenstate of the operator x with eigenvalue x.

In the basis is represented by the matrix

which is diagonalized by the eigenvectors

with the following eigenvalues

Here

is an eigenvalue of the operator Ox. In the dispersive limit, we have

Here

In this limit, the eigenvectors and the eigenvalues given by the above equations can be approximated by

Besides, assuming that the width of the atomic wavepacket is small compared with the wavelength of the stationary EMF (harmonic approximation), can be expanded to

The fact that we have chosen the point n/2 to do the expansion means that we are treating the case of blue detuning

i.e., the case in which the atoms will pass in the region of electric field node (Berman, 1997). Also we define

to be different of zero, since the potential is produced by fields counterpropagating and it difficultly will be null for real cavities. Thus, taking the dispersive and harmonic approximations, we can define the effective hamiltonian

As discussed above, the devised experiment uses three atomic levels and the third level i possesses energy below of the energy of the levels g and e , as shown in Figure 8. The frequencies

thus the transition g ^ i is very far from the resonance with the stationary mode. In this case, adopting the same reasoning sketched above, the introduction of this level modifies the effective hamiltonian given in the Equation (103)

Note that the effective coupling where

between the atom in the state i and the EMF is neglected in the above hamiltonian. In order to discuss the focalization, let us consider the following initial state

Note that the effective coupling between the atom in the state i and the EMF is neglected in the above hamiltonian. In order to discuss the focalization, let us consider the following initial state

where |^cm) stands for some state of the atomic center of mass coordinate. The atom prepared in this state interacts with the stationary field during a time interval tL. After this interval, the state of the atom will be given by

are the phase shifts accumulated by the electronic where

levels during the interaction, and are the phase shifts accumulated by the electronic

is the evolved state of the center of mass of atomic beam composed of atoms in |g) state. As Ag < 0, blue detuning, after to pass through the cavity satisfying the approaches that we use, the center of mass state gets a negative quadratic phase. An optical converging cylindrical lens with focal distance f puts a quadratic phase —kx2/(2f) on the electromagnetic beam (Saleh & Teich, 1991). By analogy, a thin lens for atoms should put a phase of the type —kpx2/ (2fp) in the atomic beam, where kp = mvz/his the atomic wave number and fp the corresponding focal distance. If we compare this phase with the phase in the Equation (107), we get

This expression is the focal distance for a thin classical lens. Different from Equation (82) to thin quantum lens, this expression does not have a explicit dependence with photon number of the field mode.

The Rayleigh range z’r and the beam waist wQ of the focused atomic beam also can be calculated using the analogy with the action of lenses in electromagnetic beams considering that the incident beam has plane wavefronts (Saleh & Teich, 1991)

where zr and Wq are the Rayleigh range and the beam waist of the incident beam, respectively, and fp is the focal distance of the atomic lens.

Ramsey interferometry with focused atomic beam and Gouy phase

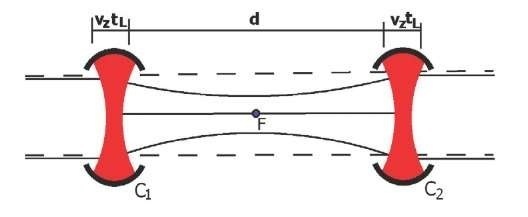
In order to experimentally observe this effect we propose an experiment with a focused Gaussian atomic beam. We will use a cylindrical focusing in the x direction, without changing the beam wavefunction in the y direction, what makes the total Gouy phase be n/2. By the analogy of the Schrodinger equation with the paraxial Helmholtz equation (Yariv, 1991; Snyder & Love, 1991; Berman, 1997; Marte & Stenholm, 1997; da Paz et al., 2007), we see that the cavities act on the |g) component of the atomic beam as cylindrical lenses with focal distance fp. If we have fp = d/2, where d is the distance between the cavities Q and C2, the system will behave like the illustration in Figure 9. The cavity C1 will transform the |g) component of the wavefunction in a converging beam with the waist on a distance d/2 (represented by solid lines). After its waist, the beam will diverge until the cavity C2. The |g) component of the wavefunction on the position of cavity C2 will have the same width and the opposite quadratic phase of the state m (x) above, so the cavity C2 will transform the divergent beam in a plane-wave beam again. The \i) component of the wavefunction, on the other hand, propagates as a plane-wave beam all the time (represented by dashed lines), as its interaction with the field of the cavities C1 and C2 is considered to be very small.

Fig. 9. Illustration of the operation of the cavities C1 and C2 as thin lenses for the atomic beam. The dashed lines represent the waist of the atomic beam if the cavities are empty. If a field is present, the solid lines represent the waist of a beam composed by atoms in the state |g). F denotes the focus region. On the other hand, if the beam is composed by atoms in the state |i), the waist does not change significatively.

By virtue of the |g) component acquires a /2Gouyphase due to the cylindrical focusing that is not shared by the \i) component, the interference pattern will be (da Paz et al., 2011)

The difference on the positions of the minimums and maximums of the patterns, one constructed when the field that forms the atomic lenses is present on the cavities C1 and C2 and other when the field is removed, should attest the existence of the Gouy phase for matter waves.

Experimental parameters and discussion

As experimental parameters, we propose the velocity of the atoms vz = 50 m/s and a slit that generates an approximately Gaussian wavefunction for the atoms with

The mass of Rubidium is m = 1.44 x 10 25 kg. With these parameters, the much larger than the length of the experimental apparatus, what justifies the plane-wave approximation. On the cavities C1 and C2, we consider an interaction time between the atoms and the atomic lenses ti = 0.2 ms, that corresponds to a width vzti = 1 cm for the field on the cavities.The fact that d ^ z’r justifies our consideration that the |g) component of the beam acquires a n/2 Gouy phase. The interaction between the atomic beam and the field in the cavities C1 and C2 depends on the position x, according to Equation (103). If we do not want that photons be absorbed by the atoms, it is important that nOQk2x2/(Ag) ^ 1 for the entire beam (Scully & Zubairy, 1997). We have nOQk2w§ / (Ag) ~ 8 x 10 4 for the proposed parameters, where wq is the beam width, showing that the absorption of photons can be disregarded. The phase difference between the electronic levels is given by

where the last term is a dispersive phase that occurs because the intensity of the electric field is not exactly zero in the node x = n/2 for real cavities. In this case is important that the cavities C1 and C2 have a large quality factor Q. In fact, the ratio between the maximum and the minimum of intensity in a cavity should roughly be the quality factor Q. So the |g) component of the beam also acquires a phase nOj^tL/ (AgQ) on the passage in each cavity, and this phase will be added to the accumulated Gouy phase. If we want that this undesired phase be smaller than Gouy phase, we need Q > 106 for our proposed parameters. This can also be experimentally achieved (Raimond et al., 2001; Nogues et al., 1999; Gleyzes et al., 2007).

Conclusion

From the strict theoretical point of view we have used the formal analogy between matter and light waves to show that the well known Gouy phase in the context of classical optics, besides its geometrical character, reflects correlations of the same sort a free particle obeying a matter wave equation. Conversely we have seen that matter waves may also present the exact analogous to the Gouy phase of quantum optics and elaborated an experiment to measure it. We hope this work might encourage the groups with the appropriate facilities to realize the experiment and, who knows, find important applications for this matter phase. The verification of the Gouy phase in matter waves has the possibility to generate a great amount of development in atomic optics, in the same way as the electromagnetic counterpart Gouy phase had contributed to electromagnetic optics. For instance, it can be used to construct mode converters for atomic beams and trapped atoms, with potential applications in quantum information.