Gouy Phase and Matter Waves (Electromagnetic Waves) Part 2

Covariance axp and Gouy phase

In this section, we calculate the covariance between position and momentum and the Gouy phase for fullerenes molecules considering the free Schrodinger equation. We calculate the phase and show that it is also related to the covariance axp as well as in the case of pure Gaussian states.

Starting from the determinant of the covariance matrix for mixed Gaussian state, Equation (42), we can express axp in terms of the beam width, i.e.,

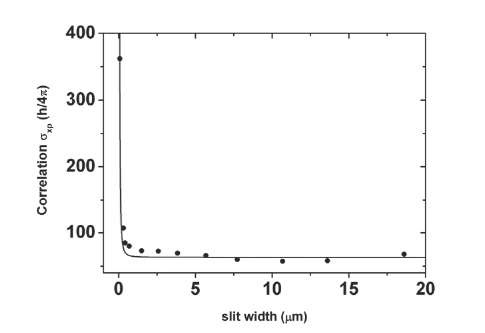
where Wfwhm is measured in the laboratory. The curve for axp, obtained with experimental data of the Ref. (Nairz et al., 2002) through the Equation (45), is showed in Figure 5 and compared with the theoretical value, Equation (41).

Fig. 5. Covariance axp as a function of slit width. Solid curve corresponds to our calculation, Equation (41), and the points were obtained of experiment reported in Ref. (Nairz et al., 2002) through the Equation (45). The parameters are the same of Figure 4.

Gouy phase for a mixed Gaussian state

A more recent definition justifies the physical origin of the Gouy phase in terms of space enlargement, governed by the uncertainty relation, of a beam whose transverse field distribution is a Gaussian function (or arbitrary) (Feng & Winful, 2001). According to Equation (11) in Ref. (Feng & Winful, 2001) the Gouy phase ^ (t) and the beam width B (t) for a pure Gaussian state of matter waves are related by the expression

Here, we conjecture, based on the obtained results, that this definition holds for partially coherent Gaussian states since the spread of these states is also governed by the uncertainty relation. Thus, for a state given by Equation (34), the Gouy phase is

where the factor ^ appears because we are working in one dimension. Note that, again y.(t) is related to ax„ and is affected by the partial coherence of the initial wave packet, i.e.,

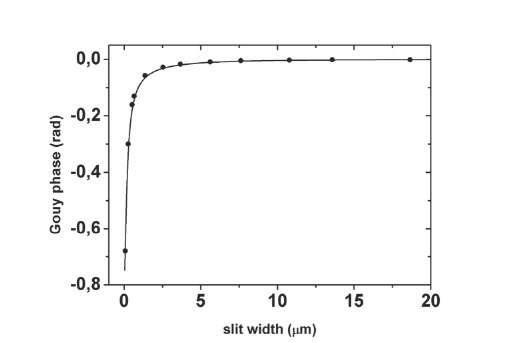
In Figure 6, we show the phase extracted from Equation (48). As expected, the variation in phase is ^/4, because we are dealing with a one-dimensional problem of diffraction and the propagation of the beam will be from t = 0to t = z/vz (Feng & Winful, 2001). This result shows that the existence of a Gouy phase is compatible with the experimental data involving diffraction of fullerene molecules. It is an indirect evidence of the Gouy phase for matter waves (da Paz, 2011; da Paz et al., 2010).

Quantum lens and Gouy phase for matter waves

In the previous section, we have shown an indirect evidence for the Gouy phase for matter waves based on the analogy existent between the paraxial equation for wave optics and

Fig. 6. Gouy phase as a function of slit width. Solid curve corresponds to our calculation, Equation (47), and the points were obtained of experiment reported in Ref. (Nairz et al., 2002). The parameters are the same of Figure 4.

Schrodinger equation for matter waves (da Paz, 2011; da Paz et al., 2010). Due to this formal similarity a question which arises naturally is if a similar phase anomaly may occur in the region around the focus of an atomic beam. In order to answer this question, in this section we present the evolution of an atomic beam described by a Gaussian wave packet interacting dispersively with a cavity field (da Paz, 2011; da Paz et al., 2007).

The model we use is the following (Averbukh etal., 1994; Rohwedder & Orszag, 1996; Schleich, 2001): consider two-level atoms moving along the Oz direction and that they penetrate a region where a stationary electromagnetic field is maintained. The region is the interval z = —Lc until z = 0. The atomic linear moment in this direction is such that the de Broglie wavelength associated is much smaller than the wavelength of the electromagnetic field. We assume that the atom moves classically along direction Oz and the atomic transition of interest is detuned from the mode of the electromagnetic field (dispersive interaction). The Hamiltonian for this model is given by

where m is the atom mass, px and x are the linear momentum and position along the direction Ox, a" and a are the creation and destruction operators of a photon of the electromagnetic mode, respectively. The coupling between atom and field is given by the function g(x) = a£2 (x) where a is the atomic linear susceptibility, a = where p2 is the square of the dipole moment and A is the detuning. E(x) corresponds to the electric field amplitude in vacuum. The effective interaction time is tL = ^, where vz is the longitudinal velocity of the atoms. The dynamics of the closed system is governed by the Schrodinger equation

At t = 0 the state of the system is given by a direct product of the state corresponding to the transversal component of the atom and a field state

The field state can be expanded in the eigenstates of the number operator a a

When atom and field interact the atomic and field states get entangled. We can then write

where

or, if one defines

the Equation (53) takes the form

Next, we will use the harmonic approximation for g(x) which is a fine approximation provided the dispersion of the wavepacket in the transverse direction b0 is much smaller than the wavelength of the electromagnetic field mode A (Schleich, 2001). Taking the main terms of the Taylor expansion of the function g(x),

we get

where xf = —g\/2g2 and O2 = ng2/m. In order to obtain focalization of the atomic beam it is crucial that the initial state be compressed in momentum since this initial momentum compression is transferred dynamically to the x coordinate and a focus can be obtained (da Paz et al., 2007; Rohwedder & Orszag, 1996). In fact, the momentum compression is a necessary condition in optics to obtain a well defined focus (Saleh & Teich, 1991).

Time evolution

According to Bialynicki-Birula (Bialynicki-Birula, 1998), the general form of a Gaussian state in the position representation, is given by

where x and p are the coordinates of "center of mass" of the distribution in phase space and u and v give the form of this distribution.

A dynamic governed by a Hamiltonian quadratic in position and momentum keep the Gaussian shape of a Gaussian initial state. This is the case of the problem treated here. The atomic motion can be divided into two stages: the first, the atom undergoes the action of a harmonic potential when it crosses the region of electromagnetic field while, in the second part, the atom evolves freely. In the two stages, the Hamiltonian governing the evolution are quadratic in atomic position and momentum [cf.Equation (57)]. Since the initial atomic state is Gaussian, we can consider that throughout evolution, such state will preserve the form given by Equation (58). In this case, the parameters x, p, u and v are functions of time, and their respective equations of motion can be derived from the Schrodinger equation. Consider a particle of mass m moving under the action of a harmonic potential. The natural frequency of this movement is On. The Hamiltonian governing this dynamic is given by

In position representation, the evolution of the state ^ of the particle is governed by the Schrodinger equation

Suppose that the initial state of the particle is Gaussian. We obtain the equations of motion for the parameters x, p, u and v by substituting the general form (58) in equation above, grouping the terms of same power in (x — x), and then separating the real and imaginary parts. This procedure takes six equations for the four parameters mentioned. The system is therefore, "super-complete". Eliminating such redundancy, the equations of motion are the following

where we define K = u + iv. Here, the dots indicate time derivation. Note that the equations of motion for the coordinates of the centroid of the distribution are equivalent to the classical equations of movement to the position and momentum of a particle moving in a harmonic potential.

A important observation must be made here. One of the two equations removed is not consistent with the others in (61). This equation is the following:

To see this, just replace the expressions (61a), (61b) in the above equation. We obtain u = 0, which makes no sense, since u represents the inverse square of the width of the Gaussian package. The only way to "dribble" this inconvenience is to redefine the general state as

where O is a real function of time. This global phase, in general neglected (see, e.g., (Bialynicki-Birula, 1998; Piza, 2001)), ensures the consistency of the equations of motion because, in addition to Equations (61), we must have

0/2 is known as Gouy phase. Equation (64) relates the Gouy phase with the inverse square of the beam width . The same result was obtained for light waves transversally confined in Ref. (Feng & Winful, 2001).

Focalization of the atomic beam

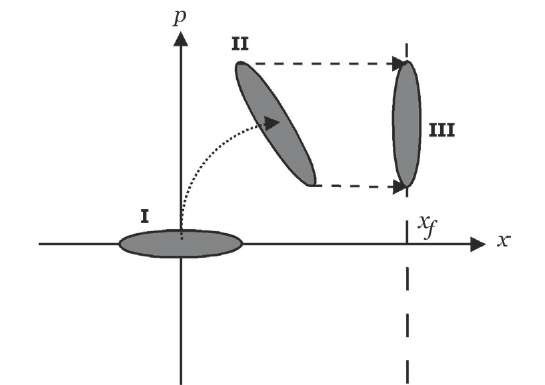
In Figure 7 we illustrated how the quantum lens work out. We consider that a initial Gaussian state compressed in the momentum (region I) penetrates in a region where a stationary electromagnetic field is maintained (region II). The atoms and the field inside the cavity interact dispersively. Dispersive coupling is actually necessary to produce a quantum lens, because the transitions cause aberration at the focus (Berman, 1997; Rohwedder & Orszag, 1996; Schleich, 2001). When the atomic beam leaves the region of the electromagnetic field, the atomic state evolves freely and the compression is transferred to the position (region III). Let us assume, as an initial atomic state, the compressed vacuum state

For the parameters x, where b0 is the initial width of the packet and

Fig. 7. Initial atomic compressed state in momentum . The evolution inside the cavity rotates the state and transfer the compression to the position.

 

and

for the initial conditions

Also, from Equation (68) we obtain

Now u 1 is the width of the gaussian wavepacket squared. At this stage

When the atomic beam leaves the region of the electromagnetic field, the atomic state evolves freely. The equations of motion can be obtained analogously and we get for t > tL

The focus will be located in the atomic beam region where the width of the wavepacket is minimal. In other words, when u(t > tL) be a maximum there will be the focus. This will happen when the function

attains its minimum value. The time for which its derivative vanishes is given by

therefore the focus is located at

The width of the Gaussian beam that passed through the lens, can be written as

where we define

and

The line was used here to differentiate the beam parameters after the focalization of their parameters before the focalization. We see that the waist of the beam is increased by factor M and the package time aging is increased by the M2 (not confuse with the quality factor Mp). In optics, the amount M is known as magnification factor (Saleh & Teich, 1991). If the state is not initially compressed, i.e., if bn = b$, does not exist focalization and in this case b’0 = b0 and r0 = T0 as we can seen by the Equations (79), (80) and (81).

If we consider an interaction time of atoms with cavity field ti very small, we have the so called thin lens regime. Because when the interaction time is very small, the movement of atoms along the transverse direction is also very small, i.e., the average transverse kinetic energy of atoms is much smaller than the average potential energy (Q(x)} produced by field, ym < (Q(x)} (Averbukh etal., 1994). The rotation angle of the atomic state caused by the interaction with the cavity field pn = Onti is directly proportional to the interaction time, thus, if ti is too small, pn will also be very small. If we consider tyn < 1 and an initial atomic state compressed in the momentum with bn/b$ ^ 1, the expression for the focal distance, equation (77), acquires the simple form (Schleich, 2001)

Phase anomaly

If we integrate the equation of motion (64) for O considering the expression for B’ (t) given by the Equation (78), we obtain

The integration interval is taken from tf to t, because the Gouy phase is the phase of the Gaussian state relatives to the plane wave at the focus, i.e., at the focus the Gaussian state is in phase with the plane wave (Saleh & Teich, 1991; Boyd, 1980; Feng & Winful, 2001). At the focus, y = 0, as expected. Therefore, the Gouy phase of the atomic wave function undergoes a change of n/2 near the focus tf. The fact that this variation is only n/2, in contrast with the value of n for the light, is due to the fact that the quantum lens focuses the atomic beam in the Ox direction, keeping the Oy direction unperturbed (i.e., the electromagnetic field acts as a cylindrical lens).

Experimental proposal

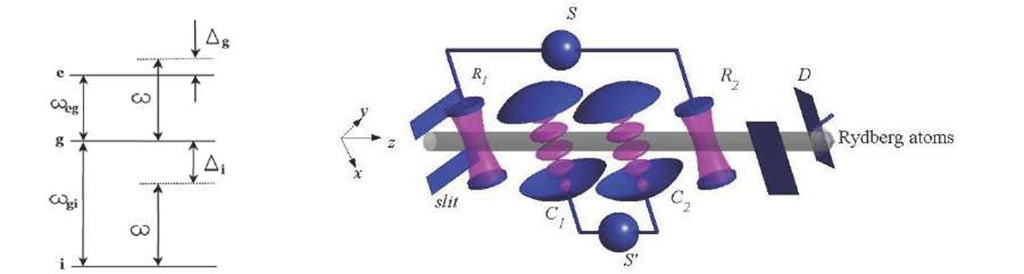
Consider a Rydberg atom with a level structure given in Figure 8 (left). Three Rydberg levels e, g, and i are taken into account. The transition between the states e and g is slightly detuned with a stationary microwave field stored in two separated cavities with frequency <x>, Cj and C2, and completely detuned with the transition g ^ i. These cavities are placed between two Ramsey zones, R\ and R2, where a microwave mode quasi-resonant with the atomic transition g ^ i is stored (see Figure 8). If the electronic atomic state involve the levels i or g, the field in both Ramsey zones are adjusted to imprint a n/2 Rabi pulse on the internal state of the atom. Then, after the Ramsey zones, the electronic state changes as

and

Fig. 8. On the left, atomic energy levels compared with the wavelength of the field inside the cavities C1 and C2. On the right, sketch of the experimental setup to measure the Gouy phase for matter waves. Rydberg atoms are sent one-by-one with well-defined velocity along the z-axis. A slit is used to collimate the atomic beam in the x-direction. The Ramsey zones R^ and R2 are two microwave cavities fed by a common source S, whereas C1 and C2 are two high-Q microwave cavities devised to work as thin lenses for the atomic beam. The field inside these cavities is supplied by common source S. The state of each atom is detected by the detector D.

The experimental setup we propose to measure the Gouy phase shift of matter waves is depicted in Figure 8 (right). This proposal is based on the system of Ref. (Raimond et al., 2001). Rubidium atoms are excited by laser to a circular Rydberg state with principal quantum number 49 (Nussenzveig et al., 1993; Gallagher, 1994), that will be called state |i), and their velocity on the z direction is selected to a fixed value vz. As it was stated before, we will consider a classical movement of the atoms in this direction, with the time component given by t = z/vz .A slit is used to prepare a beam with small width in the x direction, but still without a significant divergence, such that the consideration that the atomic beam has a plane-wave behaviour is a good approximation.

If we disregard the cavities C1 and C2, the setup is that of an atomic Ramsey interferometer (Ramsey, 1985). The cavity R^ has a field resonant or quasi resonant with the transition |i) ^ |g) and results in a n/2 pulse on the atoms, that exit the cavity in the state (|i) + |g))/\/2 (Raimond et al., 2001; Ramsey, 1985; Kim et al., 1999; Gerry & Knight, 2005). After passing through the cavity R1, the atoms propagate freely for a time t until the cavity R2, that also makes a n/2 pulse on the atoms. Calling hand hthe energy of the internal states |g) and |i) respectively, wr the frequency of the field in the cavities R1 and R2 and defining Wgi = — Mi, the probability that detector D measures each atom in the |g) state is (Raimond et al., 2001; Ramsey, 1985; Nogues et al., 1999)

Upon slightly varying the frequency wr of the fields in cavities R1 and R2, the interference fringes can be seen (Raimond et al., 2001; Ramsey, 1985; Nogues et al., 1999).