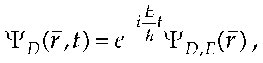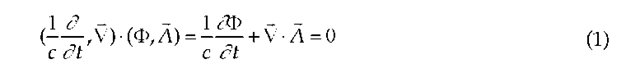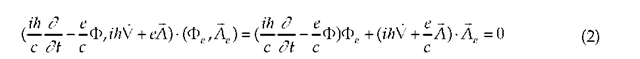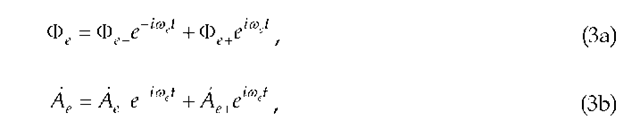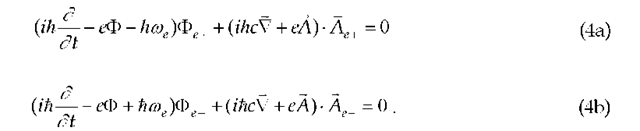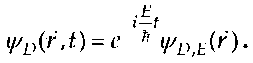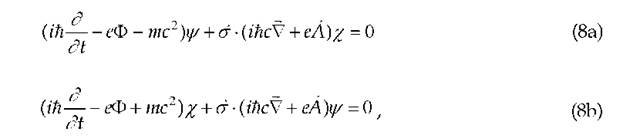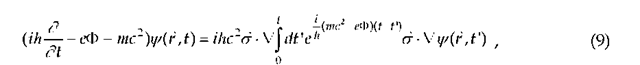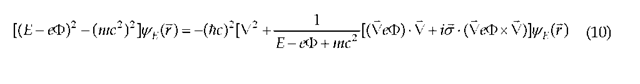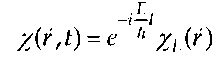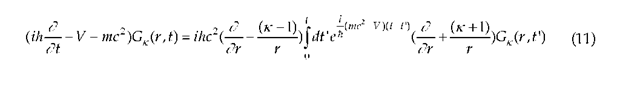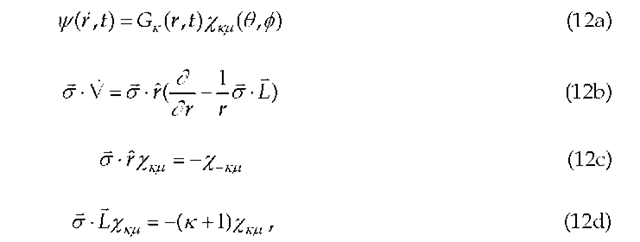Introduction
The quantum theory of matter does not describe real matter until electromagnetic theory is used to account for such diverse radiative phenomena as spontaneous emission and the shift of quantum energy levels. Classical electrodynamics fails to account quantitatively for these radiative effects in the structure of matter. Quantum electrodynamics (QED) does successfully account for radiative effects in the structure of matter once an infinite contribution to the energy, which diverges linearly with electromagnetic-wave frequency, is subtracted from the theory based on physical argument that such contribution is already included, to zeroth order in perturbation theory, in the description of a radiative as opposed to a nonradiative or bare electron. This mathematical procedure is known as mass renormalization and introduces the concept that total mass comprises both material and electromagnetic contributions, neither of which is observable by itself.
In Section II of this paper a theory is presented which describes both the material and radiative properties of matter in a single, inseparable form. We show that the time-domain relativistic-wave equation of Paul Dirac can be inferred from the Lorentz invariant obtained from the scalar product of the electron’s four-momentum and an electromagnetic four-potential, once an electromagnetic carrier-wave frequency is formally identified with the rest-mass energy of the electron divided by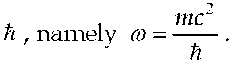 
(The scalar product of two four-vectors always gives a Lorentz invariant such that the present derivation proves the Lorentz invariance of Dirac’s equation in a single step. In the standard treatment [1], in which the Dirac Hamiltonian is the scalar product of two operator four-vectors, a second step is required to prove the Lorentz invariance of the wave equation itself.) Our derivation elucidates a long-studied problem in the literature of the identity of Dirac’s equation with the spinorial form of Maxwell’s equation [2-5]. The value of CO given above is just the cut off of the electromagnetic frequency used in QED to insure the finite value of the logarithmically-divergent contribution to the energy, which is the only divergent term remaining after the term linearly divergent in the frequency has been removed by mass renormalization. In summary Dirac’s time-domain relativistic wave equation is reinterpreted to be an equation which accounts for both the material and radiative properties of matter.
In Section III we provide an analytic proof that Dirac’s temporally harmonic solution of his equationis equivalent to solving temporally coupled equations by adiabatic elimination, which is a widely-used approximation method to solve temporally coupled equations in the optical-physics literature. In a wordDirac’s temporally harmonic solution is approximate, but his solution ofthe resulting time-independent or energy-domain equation, which is astaple of the relativistic quantum mechanics literature, is exact.The current interpretation of Dirac’s theory as describing only the material properties of matter derives from Dirac’s solution of his time- domain equation using the harmonic substitution,
albeit this form, since it constrains all four components of his energy-domain vector wave function 
to oscillate in time at a single frequency 
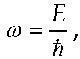is obviously not the general solution. The same harmonic form however exactly solves Schroedinger’s time-domain equation and thus gives a result which is compatible with the way quantum theory evolved as a matter-only theory without radiative effects until augmented by QED.
In Section IV numerical results are presented for the general solution of Dirac’s time-dependent equation. Fourier analysis of the generaltime-dependent solution shows that the spectrum of quantum states for the Coulomb problem comprises coupled positive- and negative-energy states. The wave function is a mixture of bound and continuum states, with an unbound component propagating away from the atom in a manner which satisfies the Lorentz-invariant relationship or causality between position and time, r**2 – (ct)**2 = 0. The unbound behavior has long been known as Zitterbewegung for a free electron, and here we show its counterpart for the Coulomb problem. In view of the Dirac-Maxwell relationship elucidated in Section II we postulate that the physical interpretation of Zitterbewegung is the emission of a photon with energy of order 2mc**2 due to the presence of empty negative-energy states in the general time-dependent solution. Dirac’s artifice of filling up the negative-energy levels with electrons to stabilize the atom is not available in the general time-dependent solution.
In Section V equations of motion for the photon are given. In Section VI subatomic bound solutions are discovered which are expected due to the temporally second-order nature of the time-domain Dirac equation. Subatomic bound solutions do not exist for Dirac’s time-independent equation (hereafter called standard Dirac theory) due to his use of the single-frequency temporally harmonic form discussed in Section III. Thus the existence of a complex neutron cannot be ruled out in the case of the general time-dependent solution as it was earlier in the case of standard Dirac theory [6]. These solutions resemble known Dirac energy-domain functions for Z > 137. The spectral content of these solutions comprises a spectral peak at -mc**2 for an electron and a spectral peak at +mc**2 for a positron – yes this state exists for a positive Coulomb potential. An electron can thus make an upward transition into the positive-energy continuum with transition energy 2mc**2, as in standard Dirac theory, while a positron can make a downward transition into the negative-energy continuum with transition energy -2mc**2. The upward transition is considered to be a matter transition, while the downward transition is considered to be an anti-matter transition.
Maxwell-Dirac equivalency
There exists a physical equivalency between Dirac and Maxwell theories which can be stated as follows. It is well known that Lorentz’ equation is the Lorentz invariant formed by taking the scalar product of the four-gradient and the electromagnetic four-potential,
Recall that the scalar product of four-vectors is always a Lorentz Invariant. One may postulate that a four-potential exists for the electron, such that an electron equation of motion can be written as the Lorentz invariant formed by taking the scalar product of the electron’s four-momentum and the electron’s four-potential,
The electron scalar and vector potentials can be written in the form of carrier-wave expansions,
from which on substituting Eqs. (3) into Eq. (2) and separately setting the coefficients of the exponential factors equal to zero, we obtain,
we obtain Dirac’s equation On setting
Identically if the carrier-wave energy is equal to the rest-mass energy 
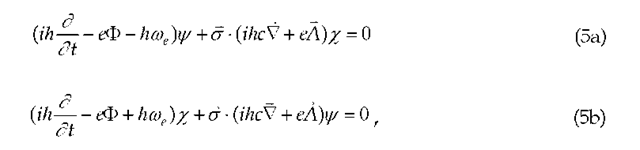
where a is Pauli’s vector. Unlike the classical electromagnetic potentials, which are real, the electron’s potentials are complex. This is obvious when we notice that the + and -envelopes are not complex or Hermitian conjugates of one another.
An electromagnetic contribution to the mass of the electron due to the quantum radiation field associated with its motion is a well known concept in QED. Indeed the carrier-wave frequency of the electron’s four-potential [Eqs. (3)] is equal to mc**2/hbar, which is the high-frequency cut off for the quantum radiation field assumed in QED atomic structure calculations. The present derivation of Dirac’s equation suggests thatthe total mass of the electron is electromagnetic in nature. This result is consistent with a previous result in which the charge of the electron was derived from Maxwell’s equations [7].
Adiabatic nature of Dirac’s solution of his equation
Although the time-dependent Dirac equation can be written in the Schroedinger form,
is Dirac’s four-component vector wave where HD is the Dirac Hamiltonian and 
function, it does not follow that the energy-domain equation can be written in the Schroedinger form,
oscillate in time at a single frequency unless one requires that all components of 
oscillate in time at a single frequency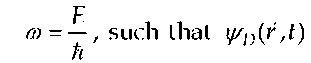 
has the harmonic form
The requirement does not hold in the general time-dependent solution of a vector wave function whose components are temporally coupled.
Eqs. (5) are rewritten in the standard Dirac form,
where a is Pauli’s vector and , % are the large, small components of Dirac’s four-component wave function . Eq. (8b) can be eliminated exactly in favor of Eq. (8a) as follows,
where we have specialized to an electromagnetic field free problem by setting A = 0.
Dirac’s energy-domain solution is obtained by substituting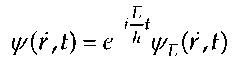 
and assuming that y/E (r, t) is slowly varying in the time compared to the exponential factor such that the integral is evaluated approximately by holding i//E(r, t’) constant at t’=t. Then the integration is performed, and the rapidly oscillating lower-limit contribution is dropped as small compared to the stationary upper-limit contribution. Such approximations to solve coupled time-dependent equations are known in the optical-physics literature as adiabatic elimination. Dirac’s second-order equation for the large component follows immediately,
where we have used the identity,
and the time has been dropped from the argument list since the approximations to the t’ integral render the wave function stationary. Clearly Dirac’s use of the Schroedinger forms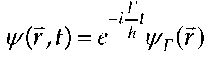 
and
to write the energy-domain form of his coupled time-dependent equations [Eqs. (8)] rests on an implicit assumption that adiabatic elimination of one of these equations in favor of the other is an accurate approximation. On other words the Schroedinger form does not hold exactly in the case of a vector wave function whose components are temporally coupled.
Dirac’s harmonic ansatz for his time-dependent equation gives him aenergy-domain equation which is exactly solvable for the free-electron and Coulomb problems. The Schroedinger form of the temporal solution, which is exact for Schroedinger’s scalar wave equation but not for Dirac’s vector wave equation, is in effect a form of calibration of Dirac theory to Schroedinger theory and has cast Dirac theory in the limited role of "correcting" Schroedinger theory primarily for relativistic effects in atomic structure. Probably as a result of its restricted use in electron physics, time-domain Dirac theory until recently had not been used to discover the a priori physical basis for Fermi-Dirac statistics [8], which is a spin-dependent phenomenon. The history of quantum mechanics instead followed a path of ensuring that Schroedinger wave functions satisfy Fermi-Dirac statistics on the basis of experimental observation and not a priori theory by using the Slater determinantal wave function to solve Schroedinger’s wave equation for many electrons, even though Schroedinger theory, in which particle spin is absent, contains no physical basis for Fermi-Dirac statistics. One must instead turn to time-domain Dirac theory and the Dirac current to discover the physical basis for Fermi-Dirac statistics, which is elucidated using spin-dependent quantum trajectories [8]. Richard Feynman [9] once asked if spin is a relativistic requirement and then answered in the negative because the Klein-Gordon equation is a valid relativistic equation for a spin-0 particle. The correct answer is thatspin is a relativistic requirement to insure Lorentz invariance in a vector-wave theory such as the Dirac or Maxwell theories. In the sense that Fermi-Dirac statistics depends critically on spin and yet is a phenomenonof order (Zc)0, where c is the speed of light and Z is the atomic number, it would appear that authors [10] are misguided who present the quantum theory of matter as fundamentally based on Schroedinger theory as augmented by Dirac theory for "relativistic corrections" of order Z4c-2 due to the acceleration of an electron moving near a nucleus with atomic number Z.
Genera solution of Dirac’s time-domain wave equation
In this section the general time-dependent solution is presented free of any harmonic bias.
Solving the Coulomb problem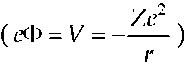 
the radial form of Eq. (9),
follows from the well-known substitutions,
where the angular functions are Dirac’s two-component spinors.Eq. (11) is solved numerically in the variables r and ct for the hydrogen-like ground state ( k = -1) with Z=70, starting for mathematical convenience with a Schroedinger wave function at initial time and using the trapezoid rule to evaluate the integral. It is found that the evolved wave function is insensitive to the starting function at initial time.
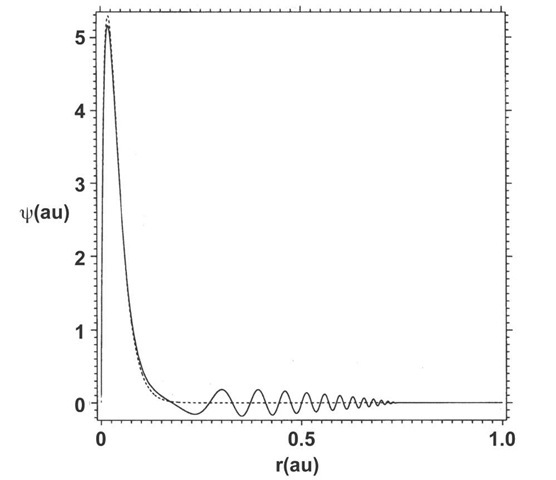
At the point t=t’ the Crank-Nicolson implicit integration procedure is used in order to insure that the time integration of the equation itself is unconditionally stable. Fig. 1 shows the spectrum of states calculated from the inverse temporal Fourier transform of the wave function [11-12]. The spectrum has a strong peak in the positive-energy regime and a weak peak in the negative-energy regime, which lies in the negative-energy continuum and thus accounts for the unbound tail (Fig. 2). This temporally expanding tail appears to be the Coulomb counterpart of the Zitterbewegung solution calculated by Schroedinger [13] using the time-dependent Dirac equation for a free electron.
Fig. 2 shows the real part of radial wave function times r. Notice that the wave function is unusual in that it behaves like a bound state close to the nucleus but yet is unbound with a small-amplitude tail along the r axis whose length is equal to ct. In other words the tail propagates away from the nucleus at the speed of light. Nevertheless I have normalized the wave function for unit probability of finding the electron within a sphere of radius rmax. The amplitude of the interior portion flows with time between the real part (Fig. 2) and imaginary part of the wave function such that the probability density is steady within the radius of the atom. (ct)max is chosen to be three-fourths of rmax in order that the propagating piece of the wave function stays well away from the grid boundary at rmax. Calculations show that the results are Insensitive to rmax and therefore to (ct)max as long as rmax is well outside the region represented by the bound piece of the wave function, that is well outside of the radius of the atom as represented by standard Dirac theory. Notice that if the dynamical calculation were extended to very large times, then the wave function would fill a verylarge volume. In principle after a sufficient time the wave function could fill a volume the size of the universe although its interior part would remain the size of an atom. What is the physical interpretation of Zitterbewegung? In view of theMaxwell-Dirac equivalency elucidated in Section II, we postulate here thatit is a photonic energy of order 2mc**2, which is the energy gap betweenthe positive- and negative-energy electron continua and which was identified in Section II as an electromagnetic carrier-wave energy equal to Thm . This amount of energy must be carried away from the atom in a continuous sense since there is no net loss of interior probability densityover time. The energy originates from the electron’s simulta-neous double occupancy of both positive- and negative-energy states(Fig. 4) whose energy difference is of order 2mc**2. In standard Diractheory the positive- and negative-energy levels are dynamically uncoupledsuch that Dirac assumed that electrons exclusively occupy the positive-energy levels and that the atom was stabilized by a set of negative-energy levels – the negative-energy sea – which are totally filledwith electrons such that the Pauli Exclusion Principle forbad thedownward fall of an electron from positive- to negative-energy levelsaccompanied by the emission of a photon with energy of order 2mc**2.
Fig. 1. Spectrum showing weak coupling of the positive- and negative-energy regions. The continuum edges are at E / c = ±mc au. The energy is obtained by multiplying the graphical numbers by c. A blow up of the positive energy peek shows good agreement with the eigenvalue at 17474.349, although the spectral calculation, because of the nature of the spectral determination of the eigenenergy, is not good to the number of significant figures shown.
Fig. 2. Solid: imaginary part of the solution of Eq. (6) times r for Z=50.(ct)max=0.75rmax=0.75 au. The number of ct, r grid points is 20K, 20K. Dotted: radial solution of Eq. (5) times r. The eigenvalue is found from the zero wronskian of forward and backward integrations and is equal to 17474.349 au to the number of significant figures shown in agreement with the analytic Dirac energy
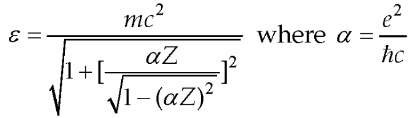is the fine structure constant.
Dotted: wave function calculated from the radial equation inferred from Eq. (5).
In the general time-domain solution presented here it appears that theatom is self-stabilizing due to the mixed material-electromagnetic natureof the electron. Recall that in Section II we postulated that the electron’sequation of motion should be the scalar product of its material four-momentum and its electromagnetic four potential. The solution of the equation of motion shows that the electron can share two ground-state material energy levels with energy conservation and without temporal decay of its quantum state as long as the energy difference between the two ground-state levels is converted to the energy of a continuously-emitted photon.
