Introduction
The majority of natural materials (rocks, soil, wood, etc.) are inhomogeneous and have a complex structure. Very often they are conglomerates or aggregates, i.e. made of small grains stuck together. This is especially typical for planetary aerosols and all types of cosmic dust (interstellar, circumstellar, interplanetary, cometary, etc.). Cosmic dust, specifically, cometary will be the main test object for this paper. This is related to the fact that cosmic dust is usually studied through remote sensing, specifically through the study of electromagnetic waves it scatters and emits. Due to this, the field of light scattering by cosmic dust has always been at the frontier of the study of interaction of electromagnetic waves with non-spherical and inhomogeneous particles.
To consider the scattering of electromagnetic waves by an object of complex structure, we will determine this object as a configuration of discrete finite constituents. They will be called inclusions in the case of inhomogeneous particles, or monomers in the case when they are constituent particles of an aggregate. Their volume is large enough that we may ignore their atomic structure and characterize their material by a specified complex refractive index, m=n+i%, whose real part is responsible for the refraction and imaginary part for the absorption of the light by the material. The surrounding medium is assumed to be homogeneous, linear, isotropic, and, in the case of aggregates, non-absorbing. Although we discuss some approximations, our consideration is based on the Maxwell equations fully describing the interaction of the electromagnetic radiation with the material. The non-linear optical effects, non-elastic scattering, quickly-changing illumination and morphology of the scattering object are beyond the scope of our study.
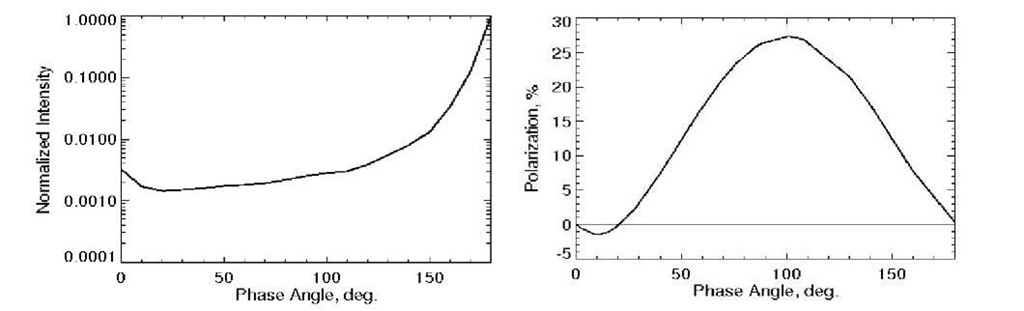
As mentioned above, our test example will be cosmic dust that typically can be presented as aggregates of submicron monomers. In the optical wavelengths they are good representatives of inhomogeneous particles with inclusions of size comparable with the wavelength, more exactly of size parameter x=2na/X> 1 where a is the radius of the monomers and X is the wavelength. The main light scattering characteristics that we use in our consideration are intensity (the first Stokes parameter, I) and linear polarization, P. The latter we describe as P=Q/I where Q is the second Stokes parameter; P>0 when the scattering plane is perpendicular to the polarization plane and P<0 when the scattering plane coincides with the polarization plane. We ignore the third Stokes parameter U since in the vast majority of the observational data the third Stokes parameter is equal to zero. We mainly consider how electromagnetic scattering affects phase curves, i.e. dependences of I and P on the phase angle, a, i.e. the angle source-scatterer-observer. It is related to the scattering angle as 180°- a. The phase curves typical for cosmic dust are presented in Fig. 1.1. Their major features that we will discuss later are forward and back scattering enhancements in the intensity phase curve and negative polarization at small phase angles. In Section 5 we also briefly consider spectral dependence of the intensity and polarization and circular polarization defined as V/I where V is the fourth Stokes parameter. All the ideas considered below can be easily extended to the case of other complex particles or media with inhomogeneities characterized by x>1.
Fig. 1.1. Typical phase curves of intensity (left) and polarization (right) for cosmic dust. Intensity is normalized to the value at 180°. Notice forward and back scattering enhancements in the intensity curve and a negative polarization branch in the polarization curve at small phase angles.
In Sections 2-4 we consider main interactions between constituents of a complex particle and describe the conditions and consequences of these interactions. The focus of our consideration is how the electromagnetic interactions change as the constituents (e.g. monomers in aggregates) become more closely packed. In Section 5 we discuss the results of rigorous computer simulations of the electromagnetic interactions. The simulations are illustrated by the results of computer modeling of light scattering by aggregates. For the modeling, we use the T-matrix approach for clusters of spheres by Mackowski & Mishchenko (1996) that, being a rigorous solution of the Maxwell equations, allows us to account for all physical phenomena that occur at the light scattering by aggregates of small particles, including far-field and near-field effects, and diffuse and coherent scattering.
Electrostatic approximation: Effective medium theories
An extreme case of electromagnetic interaction between constituents of a complex particle occurs when this interaction can be considered in the electrostatic approximation. This consideration works when a complex particle can be represented as a matrix material that contains inclusions and both the size of the inclusions and distances between them are much smaller than the wavelength. This approach implies that the inhomogeneous particle is much larger than the inclusions and can be considered as a medium. Such a medium can be presented as homogeneous and characterized by some "effective" refractive index whose value can be found if refractive indexes of the matrix and inclusion materials are known. Such an approach to the complex particles (or media) is called mixing rules or effective medium theories. After the effective refractive index is found, it can be used to model the material of the particle whose size and shape correspond to the macroscopic particle and then consider scattering of radiation by such a macroscopic particle as if it is homogeneous. Numerous mixing rules have been developed for a variety of inclusion types (non-Rayleigh, non-spherical, layered, anisotropic, chiral) and their distribution within the medium including aligned inclusions and fractal structures (see, e.g., Bohren & Huffman, 1983; Sihvola, 1999; Choy, 1999; Chylek et al., 2000). However, still the most popular remain the simplest Maxwell Garnett (1904) and Bruggeman (1935) mixing rules. The Maxwell Garnett rule represents the medium as inclusions embedded into the matrix material and the result depends upon which material is chosen as the matrix. The Bruggeman rule was obtained for a conglomerate of particles made of materials with the refractive indexes of inclusions and matrix embedded into the material with the effective refractive index. This formula is symmetric with respect to the interchange of materials and can be easily generalized for the n-component medium.
As we mentioned above, the derivation of the mixing rules is based on an assumption that the external field is an electrostatic one, which requires the inclusions to be much smaller than the wavelength of electromagnetic wave. More exactly, the criterion of the validity of effective medium theories is xRe(m)<<1 (Chylek et al., 2000) where x is the size parameter of inclusions and Re(m) is the real part of the refractive index for the matrix material. Comparison of effective medium theories with more rigorous calculations, e.g. those that use Discrete Dipole Approximation, DDA (Lumme & Rahola, 1994; Wolff et al., 1998; Voshchinnikov et al., 2007; Shen et al., 2008), and experiments (Kolokolova & Gustafson, 2001) show that even for xRe(m) ~1 effective medium theories provide reasonable results. The best accuracy can be obtained for cross sections and the worst for polarization, especially at phase angles smaller than 50° and larger than 120°.
There were a number of attempts to consider heterogeneous grains using effective-medium theories, particularly to treat cosmic aggregates as a mixture of constituent particles (inclusions) and voids (matrix material) (e.g. Greenberg & Hage, 1990; Mukai et al., 1992; Li & Greenberg, 1998b; Voshchinnikov et al., 2005, 2006). In the visual these aggregates with the monomer size parameter of x >1 are, most likely, out of the range of the validity of the effective medium theories. However, for the thermal infrared, cosmic aggregates can be treated with the effective medium theories if they are sufficiently large; remember, that the macroscopic particle should be large enough to allow considering it as a medium. If the distance between inclusions becomes larger than the wavelength, the electrostatic approximation should be replaced by the far-field light scattering (see Section 3). If the inclusions or monomers in aggregates become comparable or larger than the wavelength i.e.the criterion xRe(m)<1 is violated, cooperative effects in electromagnetic interaction between the inhomogeneities become dominating. To account for them one needs to consider rigorously the interaction of electromagnetic waves that occurs in such complex objects counting on the near-field effects (Section 4).
Far-field light scattering
The fundamental solution of the Maxwell equations as a harmonic plane wave describes the energy transfer from one point to another. The plane electromagnetic wave propagates in the infinite nonabsorbing medium with no change in intensity and polarization state. The presence of a finite scattering object results in modification of the field of the incident wave; this modification is called the electromagnetic scattering.
If the scattering object (e.g., particle) is located from the observer at such a distance that the scattered field becomes a simple spherical wave with amplitude decreasing in inverse proportion to the distance to the scattering object, the equations describing the scattered field become much simpler. This is the so-called far-field approximation. There are several criteria of this approximation (e.g., Mishchenko et al., 2006, Ch. 3.2): 2n(R-a)/A >>1, R>>a, and R>>na2/A, where R is the distance between the object and the observer and a is the radius of the object. The first relation means that the distance from any point inside the object to the observer must be much larger than the wavelength. Then, the field produced by any differential volume of the object (the so-called partial field) becomes an outgoing spherical wave. The second relation requires the observer to be at a distance from the object much larger than the object size. Then, the spherical partial waves coming to the observer propagate almost in the same direction. The third relation can be interpreted as a requirement that the observer is sufficiently far from the scatterer so that the constant-phase surfaces of the waves generated by differential volumes of the scattering object locally coincide in the observation point and form an outgoing spherical wave.
If the scattering object is an ensemble of particles, it is convenient to present the total scattered field as a vector superposition of the fields scattered by individual particles and, thus, to introduce the concept of multiple scattering. It is worth noting that at multiple scattering the mutual electromagnetic excitations occur simultaneously and are not temporally discrete and ordered events (Mishchenko et al., 2010). However, the concept of multiple scattering is a useful mathematical abstraction facilitating, in particular, the derivation of such important theories as the microphysical theories of radiative transfer and coherent backscattering (see below).
In some cases the scattering by a complex object can be considered in the far-field approximation that substantially simplifies the equations that describe the scattering. The conditions for this are the following: (1) the constituent scatterers of the complex object are far from each other to allow each constituent to be in the far-field zone of the others, and (2) the observer is located in the far fields of all of the constituent scatterers. Natural examples of such objects are atmospheric clouds and aerosols.
Diffuse light scattering
The properties of the light that is scattered by an ensemble of scatterers (e.g., small particles) only once are fully determined by the properties of the constituents. If the particles are much smaller than the wavelength, they scatter light in the Rayleigh regime and produce symmetric photometric phase function with the minimum at 90° and also symmetric, bell-shaped, polarization phase function with the maximum at 90°. For larger particles, the phase curves demonstrate a resonant structure with several, or even numerous, minima and maxima in both intensity and polarization depending on the size parameter of particles and the refractive index. Nowadays, the single scattering properties can be reliably calculated for particles of various types (e.g., Mishchenko et al., 2002).
If a complex object can be presented as a cluster of sparsely distributed particles, i.e. the far-field requirements are satisfied, the intensity of light scattered by the object is proportional to the number of constituents, N. While the number N and the packing density are increasing, the effects of mutual shadowing, multiple scattering, interference, and the interaction in the near field may destroy this dependence.
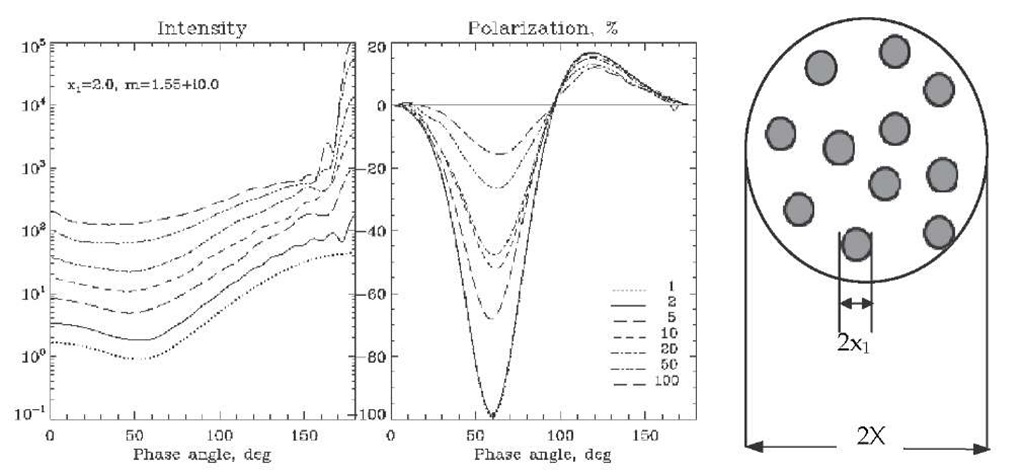
The evolution of the scattering characteristics of a cluster of separated particles with increasing number of the constituent partciels can be illustrated with the results of model calculations preformed with the T-matrix method for randomly oriented clusters of spheres (Mackowski & Mishchenko, 1996). We consider a restricted spherical volume and randomly fill it with small non-intersecting identical spheres (in the same manner as Mishchenko, 2008; Mishchenko et al., 2009a, b; Petrova & Tishkovets, 2011; see example in Fig.3.1). In Fig. 3.1 we show the absolute values of intensity and the degree of linear polarization calculated for a single small nonabsorbing spherical particle and the volume containing different number of such particles. There we define the intensity as F11QscaXr, where F11 is the first element of the scattering matrix normalized in such a way that this quantity integrated over all phase angles is equal to unity, Qsca is the scattering efficiency of the cluster, and Xv is the size parameter of the cluster calculated from the volume of the constituents as x1N1/3. When the number of particles in the cluster grows, the amplitude of the bell-shaped branches of polarization decreases, and the curves of intensity in the phase interval from 20° to 150° become flatter. If the phase curves for individual particles contained substantial interference features typical for relatively large spheres (larger than the particles considered in the example in Fig. 3.1), these features would be continuously smoothed with increasing packing density (see, e.g., Mishchenko, 2008). Such a smoothing can be interpreted as a result of the increasing contribution of multiple scattering, when many scattering events force light to "forget" the initial direction and to contribute equally to all exit directions. This also causes the depolarization effect, i.e. the light multiply scattered by an ensemble of particles is characterized by smaller values of polarization than the polarization of the light scattered by an individual particle of the ensemble. This happens since the position of the scattering plane changes at each consequent scattering, thus changing the polarization plane of the scattered light. Multiple changes that resulted from multiple scattering by randomly distributed particles randomize the polarization plane and, thus, lower the polarization of the resultant light. It is remarkable that diffuse multiple scattering is unable to change the state of polarization. As a result of this, the polarization always changes its sign at the same phase angle as for an individual particle no matter how many particles are in the cluster (Fig 3.1). Since the behavior of the diffuse multiple scattering in the sparse media is rather well investigated in the framework of the radiative transfer theory, here we only recall the main properties of the scattered electromagnetic radiation. It increases, when either the particle size, or the number of particles in the medium, or the real part of the refractive index, or the packing density grow. If the imaginary part of the refractive index increases, the contribution of the radiation scattered twice predominates. The latter is partially polarized and can strongly depend on phase angle. For densely packed clusters or media, a study of the scattering based on the diffuse scattering is not relevant as it lacks consideration of such effects as shadowing and near-field interaction (see Section 4).
Fig. 3.1. The intensity and polarization of light scattered by a single spherical particle (dotted curve) and clusters of such particles contained in the volume of the size parameter X=20. The values of the size parameter x1 and the refractive index m of the constituent particles and the number of particles in the volume are listed in the figure. The packing density of the cluster (defined as p = N x13/ X 3) grows from 0.1% to 10% (for N=1 and 100, respectively). An example of the cluster is shown on the right.
Numerous computations have shown that the light-scattering characteristics of aggregates substantially differ from those of a cluster of separated monomers and change if the structure and porosity of the aggregates change (West, 1991; Lumme & Rahola, 1994; Kimura, 2001; Kimura et al., 2003, 2006; Mann et al., 2004; Petrova et al., 2004; Tishkovets et al., 2004; Mishchenko & Liu, 2007; Mishchenko et al., 2007; 2009a; 2009b; Zubko et al., 2008; Okada & Kokhanovsky, 2009; and references therein). These changes cannot result from the diffuse multiple scattering between the aggregate monomers, which can only suppress the resonant features typical for the phase function of constituents and depolarize the scattered light. The specific shape of the phase curves shown in Fig. 1.1 is caused by more complex cooperative effects.
A striking feature in the intensity phase curve in Fig 1.1 is a strong increase of the intensity as the phase angles become larger than 160°. Development of such an increase with increasing number of the particles in the volume is evident in the plots shown in the left panel of Fig. 3.1. This strong forward scattering enhancement is caused by constructive interference of light scattered by the particles in the exact forward direction. In this direction, the waves scattered once by all the particles are of the same phase (if the particles are identical) irrespective of the particle positions (see Bohren &Huffman, 1983; Section 3.3). The oscillating behavior of the intensity curves in the forward scattering domain also points to the interference nature of this feature. In the absence of multiple scattering, this interference would result in an increase of intensity by a factor of N(N -1) as compared to the scattering by a single particle or by a factor of N2, if the non-coherent single scattered components are taken into account. Such an increase is really observed, when the packing density is small. However its development slows down with increasing packing density and practically stops, when the packing density exceeds approximately 15%. Such a behavior results from the fact that the incident light exciting a particle gets attenuated by its neighbors. This effect finally leads to the exponential extinction of light considered in the radiative transfer theory. The polarization caused by the single scattering interference in the forward scattering region is the same as that for the constituents, if they are identical.
One more interesting feature starts to develop in the intensity phase curve when the number of particles in the volume grows. This is the enhancement toward zero phase angle, which becomes noticeable at N=50 at phase angles smaller than 15°. It is accompanied by a change in the polarization state at small phase angles. These features are a typical manifestation of the coherent-backscattering (or weak-localization) effect, which is considered in the next section.
Coherent backscattering effect
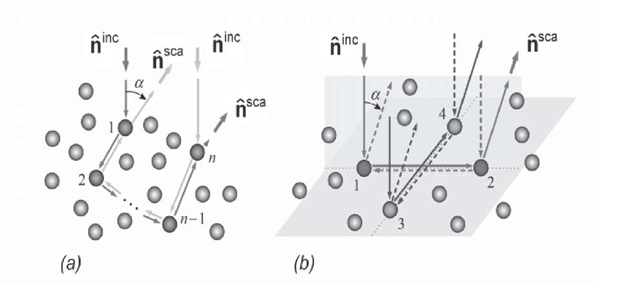
The enhancement of intensity that started to emerge in the backscattering domain (Fig. 3.1), when the packing density approached 5%, is a frequent feature of the phase curves of many scattering objects observed in laboratory (particulate samples) or in nature (regolith surfaces). This is the so-called brightness opposition effect. Explanation of its origin is illustrated in Fig. 3.2a (see Mishchenko et al., 2006 and references therein). The conjugate waves scattered along the same sequence of particles in the medium but in opposite directions interfere, and the result depends on the respective phase differences. For any observational direction far from the exact backscattering, the average effect of interference is negligible, since the particle positions are random. However, at exactly the backscattering direction, the phase difference is always zero and, consequently, the interference is always constructive, which causes the intensity enhancement to the opposition. This effect is called coherent backscattering.
Interference in the backscattering direction may manifest itself in one more effect: it may lead to appearance of a branch of negative polarization at small phase angles (the so-called polarization opposition effect). This effect is schematically explained in Fig. 3.2b (also see Shkuratov, 1989; Muinonen, 1990; Shkuratov et al., 1994; Mishchenko, 2008). Particles 1-4 are in the plane perpendicular to the direction of the incident nonpolarized light. The particles 1 and 2 are in the scattering plane, while particles 3 and 4 are in the perpendicular plane. Let us assume that the particles are small relatively to the wavelength. Then they scatter light in the Rayleigh regime; the radiation scattered by such a Rayleigh particle is positively polarized for all phase angles. For the light scattered by the pair of particles 1-2, the resultant polarization keeps the polarization plane of the single scattering, i.e. it stays positive. However, the light scattering by the pair 3-4 occurs in the plane perpendicular to the resultant scattering plane; this makes the light scattered by this pair polarized in the scattering plane, i.e. negatively. The phase difference between the waves passing through particles 3 and 4 in opposite directions is always zero, while for particles 1 and 2 such phase difference is zero only at exactly the backscattering direction and quickly changes with changing the phase angle. Consequently, the conditions for negative polarization of the scattered light are on average more favorable in a wider range of phase angles than those for positive polarization. This forms a branch of negative polarization with the minimum at a phase angle whose value is comparable with the width of the brightness peak of coherent backscattering. Since only definite configurations of particles contribute to this effect, polarization opposition effect is less strong than the opposition effect in intensity.
Fig. 3.2. Schematic explanation of the coherent backscattering effect.
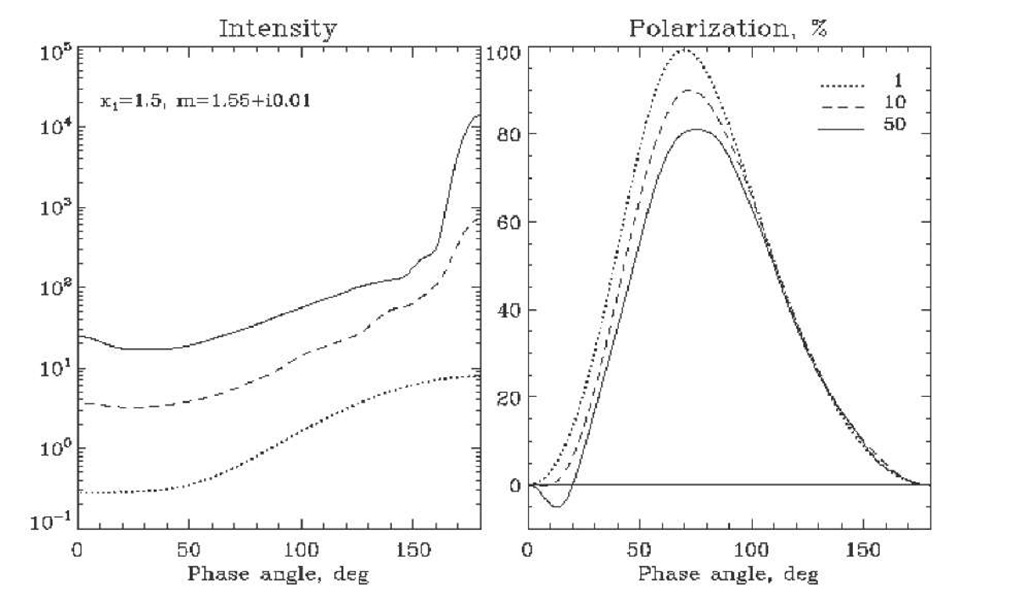
An example of such a behavior is shown in Fig. 3.3. It is seen that the formation of the intensity enhancement at small phase angles is accompanied by development of a negative polarization branch as the number of particles in the ensemble grows. Notice that the effect results from the fact that the polarization of the single-scattered light is positive. If the polarization of the single scattered light is negative, the interference results in positive polarization. If the polarization of singly scattered light changes its sign at a specific scattering angle, the interference leads to a complex angular dependence of polarization for the ensemble of scatterers as seen in Fig. 3.1.
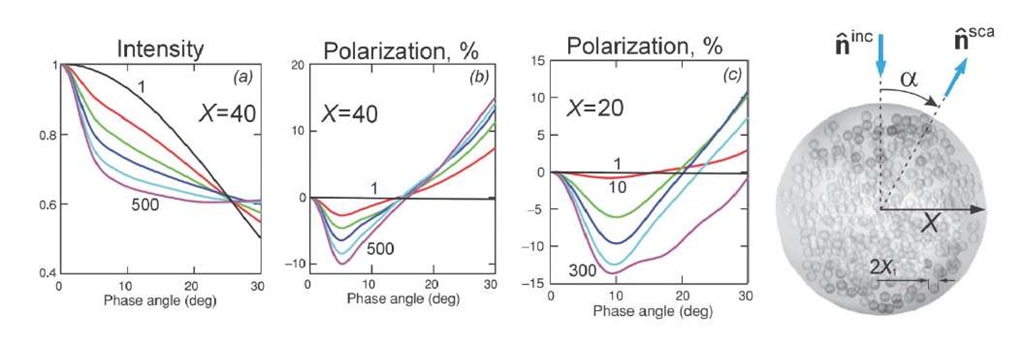
In the interference presentation of the brightness and polarization opposition effects it was clearly assumed that the scatterers are in the far-field zones of each other, since some phase and polarization are attributed to the wave scattered by one particle and exiting the other one. However, recently it has been demonstrated that the conclusion on the interference nature of the opposition effects remains also valid for more closely packed media. In Fig. 3.4 we present some results obtained by Mishchenko et al. (2009a, b). They examined the influence of the packing density on the opposition phenomena in order to determine the range of applicability of the low-packing density concept of the coherent backscattering theory to densely packed media. As in the previous example, the ensemble of varying packing density was enclosed in a spherical volume of size parameter X (shown on the right of Fig. 3.4). When the number of particles in the volume of X=40 grows (N=500 corresponds to the packing density p=6.25%), the opposition peak grows, and the branch of negative polarization becomes deeper (Fig. 3.4 a-b). At the same time, the angular width of the opposition peak (determined as the angular position of the point, where the curve changes its slope) and the angular position of the polarization minimum are almost the same and remain constant with increasing number of particles. However, as the packing density grows (in Fig 3.4c this was achieved by decreasing the volume X) the shape of the negative branch transforms. To some value of the packing density, it is asymmetric, and its minimum is shifted to opposition as predicted by the theory of coherent backscattering (Mishchenko et al., 2006 and references therein). When the packing density grows up to substantial values (Fig. 3.4c, N= 300 that correspond to p = 30%), the effects related to the interaction ofparticles in the near field become noticeable. They manifest themselves in the transformation of the shape of the negative branch and its widening, which we discuss in Section 4.
Fig. 3.3. Same as Fig. 3.1, but X=15, x1=1.5, and m=1.55+;’0.01. The numbers of particles in the volume are listed in the right top corner of the polarization plot.
Fig. 3.4 The influence of the coherent backscattering on the intensity (normalized to the value at zero phase angle) and polarization of light scattered by ensembles of nonabsorbing spherical monomers of x1=2 and m=1.32. Note that such individual monomers have polarization equal to zero in the backscattering domain and positive for the other phase angles. The size parameter of the volume X and the smallest and largest numbers of particles are shown in the plots. The geometry of the scattering ensemble is shown on the right.
Some experimental facts
The above described opposition phenomena - a nonlinear enhancement of brightness to opposition and a negative branch of linear polarization of the scattered light – have been observed for cosmic dust in a variety of environments (debris disks, comets, Saturn’s rings, asteroids and satellites of planets) as well as for laboratory particulate samples. Numerous experimental studies showed that the characteristics of these effects and their phase profiles are undoubtedly connected with absorption and microphysical structure of the scattering objects. In particular, it was found that a very sharp narrow brightness peak and an asymmetric branch of negative polarization with the minimum close to zero phase angle (less than 2°) are typical of bright and porous objects (see, e.g., the review by Rosenbush et al., 2002). These strongly expressed manifestations of the coherent backscattering mechanism appear due to a rather large free path of light in such a sparse particulate medium as regolith. Since the width of the coherent peak in intensity is inversely proportional to the free path, for extremely sparse media like atmospheric clouds this peak should be very narrow and cannot be observed. This peak also cannot be observed for the media that have a small restricted volume like small aggregates, especially if they are absorbing (e.g., Etemad et al., 1987). The absence of very sharp opposition features in aggregates and other individual particles of complex structure was confirmed by both observations of the cosmic dust and laboratory measurements (e.g., Levasseur-Regourd & Hadamcik, 2003; Shkuratov et al., 2004). This effect is also seen in Figs. 3.3-3.4 when the number of monomers in aggregates is small. These particles demonstrate a moderate increase of brightness to opposition and the branch of negative polarization with a shape close to symmetric.
Astronomical observations also revealed that dark or densely packed media demonstrate wider, if any, peaks of brightness near opposition and more symmetric branches of negative polarization (e.g., Shkuratov et al., 2002; Belskaya et al., 2005). This contradicts to the theory of coherent backscattering, which predicts that the opposition effects in brightness and polarization have the same cause and should appear simultaneously. Moreover, since only certain particle configurations contribute to polarization opposition effect, it might be less pronounced than brightness opposition effect. The shadow hiding, which is usually invoked to explain the widening of the opposition brightness peaks in dark surfaces (Lumme & Bowell, 1981), cannot induce such a significant negative polarization of the scattered light (e.g., Shkuratov & Grynko, 2005). Accurate consideration of the electromagnetic field in the particle vicinity, accounting for the presence of neighbor particles in the densely packed scattering clusters allows revealing one more scattering effect – the influence of the near field, which is considered in the next section.