5.1.3
Brushless dc motors initially were designed in large numbers for spindle drives in Winchester disk drives. The early designs were three-phase, later moving to two-phase and then one-phase, due to the very slow start-up requirements, very small friction loads, and the need to reduce unit cost at all levels. The industrial and machine tool markets started with and continue to use three-phase BLDC motors in their variable-speed, variable-load, high-start-up applications. The overwhelming popularity of three-phase BLDC motors focuses this subsection toward three-phase windings. Many of the initial design activities for various winding patterns can be traced back to the 1920s and earlier based on work done on three-phase ac windings.
This subsection reviews the various winding line connections, the key winding patterns and hookups, various winding constants, and winding selection and design techniques.
Basic Winding Configurations. There are other basic decisions that must be made by the design engineer before a BLDC motor design can commence. Previously defined is the number of phases, which is three here. Next in importance is the number of poles. The use of two poles is waning, and the use of six or eight poles is increasing. Four-pole BLDC motors are among the most popular used today. Two-and four-pole BLDC motor designs are used here, but the rules for two and four poles can be extended to higher pole counts. The number of stator slots (and teeth) and the winding pattern are key design decisions. This section is dedicated to reviewing the important parameters of these two design decisions.
In a three-phase motor there are three windings or phases positioned 120° electrical apart. Figure 5.30 shows the location of 6 coils in a representative 12-slot sta-tor. A two-pole rotor (not shown) will rotate as the three windings are energized in sequence A-B-C, as A-A’, B-B’, and then C-C are energized sequentially.The three-phase winding always develops positive starting torque, no matter where the rotor starts its motion.
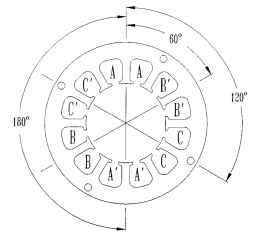
FIGURE 5.30 Basic 3-phase winding layout.
There are many winding line connections that can be used in three-phase drive systems. Figure 5.31 illustrates the various configurations. The half-wave wye is the simplest three-phase line configuration (Fig. 5.31a). It uses three power lines and one return line (four leads). The excitation is shown adjacent to the schematic in Fig. 5.31a. Only 33 percent (one lead) of the half-wave wye windings are energized at any time in operation. The second wye winding, the full-wave wye (Fig. 5.31b) has only three leads but 66 percent (two leads) of the windings are in operation simultaneously. The excitation scheme is shown to the right of the schematic.
The third major winding connection pattern is the delta, shown in Fig. 5.31c. It possesses the same excitation scheme as the full-wave wye. The delta winding configuration has been used more extensively than the wye in fractional-horsepower (<746 W) motor applications.The wye is more popular with the larger-sized integral-horsepower BLDC motor users. The final winding to be reviewed is the independent winding line connection (Fig. 5.31d). In this scheme, each winding is independent of its neighbor. The excitation scheme is more complicated, but each winding can be operated in parallel, thereby distributing the total current. The windings are still situated 120° electrical away from each other.This winding configuration has seen limited use to date.
The most popular winding line configurations are the full-wave wye and the delta. In a balanced wye configuration, the line and coil (phase) currents are equal,

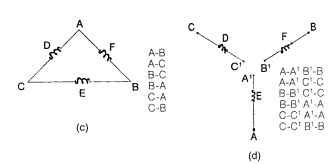
FIGURE 5.31 Popular 3-phase BLDC motor winding line connections: (a) wye (half wave), (b) wye (full wave), (c) delta, and (d) independent.
the neutral current is zero, and the line-to-line voltage is V3 times the phase voltage. In a balanced delta connection, the line-to-line and coil (phase) voltages are equal, but coil currents are 1/V3 times the line-to-line currents.
Key Winding Patterns. There are many types of winding patterns that can be utilized. Four major winding patterns are listed here:
1. Constant integral pitch—lap winding (full)
2. Variable pitch—concentric winding
3. Constant fractional pitch—lap winding for even or odd stator slots
4. Half-pitch
Each of these winding patterns has two coils per stator slot. There is one winding type designated, a consequent pole winding where there is only a single coil per slot. Consequent pole windings are very popular in single-phase ac motors of fractional-horsepower size.
Table 5.7 is revised from Veinott and Martin (1987). It displays the various sta-tor slot and rotor pole combinations along with the maximum number of parallel circuit combinations with a specific slot and pole combination. For purposes of simplicity, either 12- or 24-slot stators are used here to illustrate the various winding patterns. In one case, a 15-slot stator is used to illustrate an odd-slot fractional-pitch lap winding.
TABLE 5.7 Slots Versus Poles Versus Parallel Hookups Versus Coils per Pole per Phase
| 2 Poles | 4 Poles | 6 Poles | 8 Poles | ||||
| Coils | Coils | Coils | Coils | ||||
| per | per | per | per | ||||
| Slots | phase | phase | phase | phase | |||
| or | per | per | per | per | |||
| coils | Circuits | pole | Circuits | pole | Circuits | pole | Circuits pole |
| 6 2 1 | — | — | — | ||||
| 9 | 1 | — | — | — | |||
| 12 | 2 | 241 | — | — | |||
| 15 | 1 | 1 | 1Y, | — | — | ||
| 18 | 2 | 3 | 2 | VA | 61 | — | |
| 21 | 1 | 3Yi | 1 | NP* | X | — | |
| 24 | 2 | 4 | 4 | 2 | NP | X 8 1 | |
| 27 | 1 | 4Y, | 1 | 2Y4 | 3 | 1Y, | 11Y8 |
| 30 | 2 | 5 | 2 | 2Y-2 | NP | X | 2 1Y4 |
| 33 | 1 | 1 | 23/ | NP | X | 1 1% | |
| 36 | 2 | 6436 | 2 4 1Y | ||||
| 39 | 1 | 1 | 3Y4 | NP | X | 1 15/8 | |
| 42 | 2 | 7 | 2 | 3Y-2 | NP | X | 2 13/4 |
| 45 | 1 | 7Yi | 1 | 33/ | 3 | 2Yi | |
| 48 | 2 | 8 | 4 | 4 | NP | X | 82 |
If one uses a 12-slot stator winding, there are two full-pitch integral lap windings available, one for two poles and the other for four poles.
P x Ph = nS (5.1)
where P = number of poles Ph = number of phases S = number of stator slots n = integer number 1, 2, 3,… n
If P = 2, Ph = 3, and S = 12, then n = 2, an integer. Figure 5.30 shows the basic winding-slot pattern for a 12-slot 2-pole 3-phase 2-coils-per-pole-per-phase (n = 2) configuration. The coil pattern for this winding configuration is shown in Figs. 5.32 and 5.33 as a series wye line configuration and as a parallel wye line configuration, respectively. There are really 12 coils used in this design, but only 6 are shown.There are two 1- to 7-throw coils—one inserted on the right side (CW direction), the second inserted on the left side (CCW direction), and doubles on the other five coils also, inserted as described previously. Note the position of the teeth for the 12-slot stator. The slot pitch (adjacent slot to slot) is 360/12 or 30° mechanical or electrical. The angular location for the phase 2 winding (CW direction) is only 60°. It is supposed to be 120°. Symmetry solves the problem if 180° (polarity change) is added to the 60° to achieve 240° mechanical or electrical. So the 1, 2, 3 winding phase hookups displayed in Fig. 5.32 will yield a CCW rotation.
The series and parallel hookup options are very important from a practical aspect of magnet wire size selection. It is easier to pack smaller-sized magnet wires in a
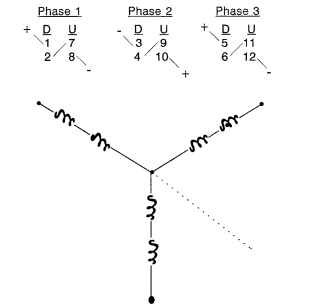
FIGURE 5.32 Series hookup for 2-pole wye-winding 12-slot brushless dc motor.
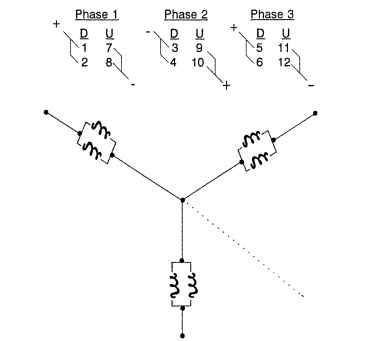
FIGURE 5.33 Parallel hookup for 2-pole 3-phase wye-winding 12-slot brushless dc motor, constant-pitch lap winding pattern.
BLDC stator slot than larger ones. Since total turns per phase are directly proportional to torque, putting all the needed turns (N per phase) in a single coil with smaller magnet wires and then paralleling the coils will yield extra space for more turns. This is a packing factor consideration.
The disadvantage of using parallel coils is that both sets of coil leads must be used to properly connect the coils (see Fig. 5.33). Figure 5.34 shows a representation of how two coils would be inserted into adjacent stator slots. Remember that there are 2 slots per coil per phase for this 2-pole 12-stator-slot winding pattern.
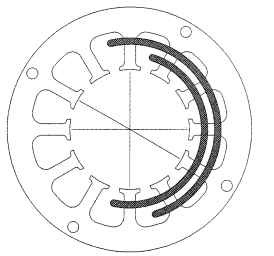
FIGURE 5.34 12-slot lamination, 2 poles, 3-phase constant-pitch lap pattern.
Figure 5.35 shows the winding pattern for a constant-pitch 4-pole 12-slot BLDC stator.There is now only one coil per pole per phase (n = 1) in this winding, as shown in the following equation:
4 poles x 3 phase = 12 slots
n = 1 coil per pole per phase (5.2)
The four coils per phase can be connected as four coils in a series hookup or four coils in a parallel hookup. It is also possible to connect two coils in series and two coils in parallel to achieve a series-parallel hookup. Figure 5.36 displays two adjacent coils inserted into the proper stator slots. Note the shorter length of these coils because the end turns are shorter while the segments of the turns (conductors) within the appropriate stator slots remain the same length. The shorter the end-turn length (which doesn’t create any torque), the better the motor design.
The variable-pitch winding was developed to reduce the stator end-turn height caused by the numerous adjacent coil crossovers by nesting the coils inside each other, as shown in Fig. 5.37. This pattern can be used only when coils per phase per pole n is 2 or greater. Figure 5.37 displays an n = 3 condition.The actual winding pattern is shown in Fig. 5.38. Since n = 2, there will be two different winding lengths or
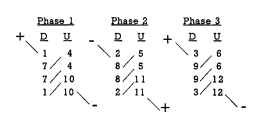

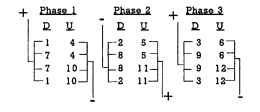
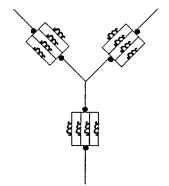
FIGURE 5.35 Winding pattern for a constant-pitch 4-pole 12-slot stator, 3-phase hookup, 30° mechanical, 60° electrical.
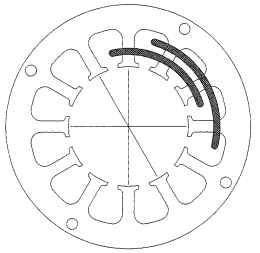
FIGURE 5.36 Constant-pitch 4-pole lap winding pattern with adjacent coil layout.
throws. The following equation describes the method used to determine the two variable winding pitches:

VSP1 = 7 and VSP2 = 5. The average of these two variable-pitch coils should equal the integral winding pitch for a 3-phase 2-pole 12-slot design, which is 6. Figure 5.39 displays the location of two adjacent coils placed in the proper stator slots. This winding pattern will reduce end-turn height and coil lengths by 10 to 15 percent.The concentric winding with variable pitch has been used extensively in larger integral-horsepower units, particularly by the various electric winding repair houses.

FIGURE 5.37 Side view of variable-pitch concentric winding pattern.
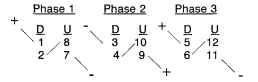
FIGURE 5.38 Variable-pitch concentric winding pattern, 2 poles, 3-phase series hookup.
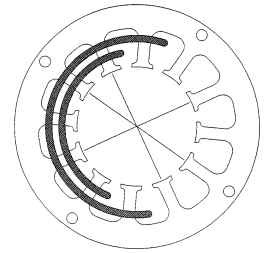
FIGURE 5.39 2-pole 3-phase variable-pitch concentric pattern.
The third winding pattern is fractional-pitch winding, which is used in many applications, particularly odd stator slots where cogging torque must be reduced. Table 5.7 identifies the fractional pitch as 1% for a 15-slot 4-pole configuration.This pattern is popular for resolver windings and some low-cog BLDC motors. The following equation yields the pitch:

Equation (5.5) identifies the winding pitch or throw as either 3 or 4. Three is selected for the pattern shown in Fig. 5.40.The starting points for the coils must meet the pattern of coil placements shown. This pattern places two adjacent coils strategically and equidistantly around the stator with each of the three phases having one set of two adjacent coils and three sets of single coils (pattern from Veinott and Martin, 1987).

FIGURE 5.40 Constant fractional-pitch odd-slot 4-pole, 3-phase series hookup. Recommended coil groups: 2-1-1-1-2-1-1-1-2-1-1-1 = 15.
As with any winding, there are advantages counterbalanced by disadvantages. The following equation defines the tooth or slot pitch of the 15-slot stator.

Now, since this design is a four-pole BLDC design, there are two full electrical cycles for one full mechanical cycle. The next equation defines the relationship between electrical and mechanical degrees for any four-pole design.
Degrees electrical = degrees mechanical x number of pole pairs
.-. Degrees electrical = 24°x 2 = 48° electrical (5.7)
A 48° electrical pitch does not equal the desired 60° pitch, so there must be torque loss.
Figure 5.41 illustrates the winding pattern for a 12-slot 2-pole fractional-pitch winding. A full winding pitch would possess a value of 6 with a throw of 1 to 7. This winding pattern has a winding pitch of 56 (fractional) or a throw of 1 to 6. This group of fractional-pitch windings has a pitch less than 1 when an even stator slot count is employed. This winding pattern is used in larger three-phase ac motors to decrease the harmonic content of both the voltage and mmf waveforms. This technique is very similar to that of short-pitch lap windings used in brush dc motors.
The final winding type is the half-pitch winding, which has the simplest winding pattern. The coil is wound directly around the stator tooth with a winding pitch of 1
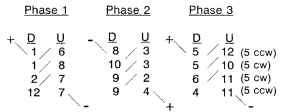
FIGURE 5.41 Constant fractional-pitch even-slot 2-pole 3-phase series hookup.
and a throw of 1 to 2. It is used extensively in step motors and switched-reluctance motors. It is also used in PM BLDC motors used in disk drives. A nine-slot eight-pole winding is very popular, as well as a nine-slot six-pole. This winding by definition is also a fractional-pitch winding. It is the most cost-effective and simplest winding with the shortest mean length of turn (MLT) and therefore the lowest resistance per coil. It does suffer from reduced torque, as all fractional pitch windings do. The various winding factors that determine the reduced torque values are reviewed in the next subsection.
Winding Factors for Different Winding Patterns. There are a number of winding factors that adjust for the peak magnetomotive force (mmf) and the winding-generated flux <) which directly leads to adjustments to the winding back emf (Ke) and peak developed torque of the BLDC motor. These factors can be identified as follows:
• Chord factor (pitch factor)
• Distribution factor (breadth factor) ^ End-turn factor (coil-length factor)

for a 12-slot 2-pole 3-phase integral-pitch winding with 2 slots per pole per phase. Veinott and Martin (1987) developed a table with the distribution factor for each major winding pattern, summarized in Table 5.8.
Table 5.9 contains the tabulated results for the Kp and Kd values for the six winding patterns presented plus a 24-slot 4-pole integral-pitch winding pattern illustrated
in Fig. 5.42.
TABLE 5.8 Summary of Distribution Factors
| Slots per pole per phase, | 3 Phase | ||
| or coils per group | 2 Phase | Conventional | Consequent pole |
| 1 | 1.000 | 1.000 | 1.000 |
| 2 | 0.924 | 0.966 | 0.866 |
| 3 | 0.911 | 0.960 | 0.844 |
| 4 | 0.906 | 0.958 | 0.837 |
| 5 | 0.904 | 0.957 | 0.833 |
| 6 | 0.903 | 0.956 | 0.831 |
| CO | 0.900 | 0.955 | 8.270 |
| 1/2 | 0.911 | 0.960 | 0.844 |
| All other fractional | 0.900 | 0.955 | 0.827 |
| slot windings |
TABLE 5.9 Summary of Kp and Kd Factors
| Slot | Slots per | ||||||||
| Stator | Winding | Winding | Winding | pitch, | pole per | ||||
| slots | Poles | type | pitch | throw | ° mechanical | phase n | Kp | KdKp | |
| 12 | 2 | Integral | 1 | 1-7 | 30 | 2 | 0.966 | 1.000 | 0.966 |
| 12 | 4 | Integral | 1 | 1-4 | 30 | 1 | 1.000 | 1.000 | 1.000 |
| 12 | 2 | Variable | 1 (average) | 1-8/1-6 | 30 | 2 | 0.966 | 1.000 | 0.966 |
| 15 | 4 | Fractional | 1/4 | 1-4 | 24 | 1 | 1.000 | 0.924 | 0.924 |
| 12 | 2 | Fractional | *8 | 1-6 | 30 | 1 | 1.000 | 0.966 | 0.966 |
| 9 | 8 | Half-pitch | 1>8 | 1-2 | 40 | 1 | 1.000 | 0.985 | 0.985 |
| 24 | 4 | Integral | 1 | 1-7 | 15 | 2 | 0.966 | 1.000 | 0.966 |
Filling the Stator Slots. The first item in filling the stator slot is to compute the area of the slot. There are many types of stator slot shapes but the trapezoidal (constant-tooth-width) slot shown in Fig. 5.30 and the round (variable-tooth-width) slot are the most popular slot shapes. One can use basic trigonometry to determine the slot area or obtain the actual slot area from the lamination vendor.
There are three methods used to compute slot area and the total volume of copper magnet wire used. They use the following units:
• Square inches (in2)
• Square mils (mil2)
• Circular mils (cmil)
The circular mils method uses the nominal diameter of the insulated wire in mils or thousandths of an inch and takes the square of this diameter, which is the circular mil value.
Area, cmil = (nominal diameter, mil)2 (5.10)
For 18 AWG (American Wire Gauge), the nominal insulated single-build wire diameter from the Phelps Dodge magnet wire chart (Table 2.76) is 41.8 mil. The
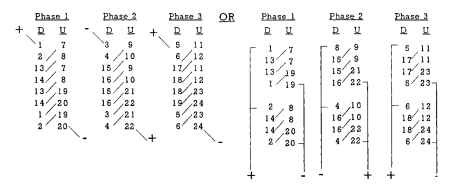
FIGURE 5.42 24 stator slots, 4 poles, 3-phase hookups 30° mechanical, 60° electrical.
wire area is 1747 cmil per Eq. (5.10). The square mils value is smaller and can be computed by modifying Eq. (5.10) to Eq. (5.11). In many cases, the wire charts compute the magnet wire’s nominal diameter without insulation coating (bare wire diameter). It is strongly recommended that the insulated wire dimensions be used.
![]()
The Phelps Dodge magnet wire chart (Table 2.76) also shows wires per square inch. The more important parameter is turns (conductors) per square inch. It yields the value of total number of turns—or, more appropriately, conductors—that can be placed in a slot, assuming 100 percent fill. Now, the most copper fill in terms of a percentage of actual turns per square inch versus 100 percent fill turns per square inch that this author has actually done by hand-insertion methods is 73 percent with 37 AWG and 63 percent with 21 AWG.
The practical limit is somewhere between 40 and 50 percent of this theoretical value depending on the type of winding machine, tooling used on the winding machine, length of stator stack, size of stator slot, etc. If one wanted to use 22 AWG, the turns (conductors) per linear inch would be 37.5 and the turns (conductors) per square inch would be 1410.
Total conductors (theoretical) = (SA) (turn/in2) Total conductors (theoretical) = 0.2192 x 1410 = 309 (5.12)
where SA = slot area
The total conductors must be an even number because 2 conductors equal 1 turn. Here the maximum value is 308 conductors with 22 AWG magnet wire. That would be 308/2 or 154 turns, since two coils are represented in every stator slot. Based on a practical slot fill of 45 percent, the maximum number of turns would probably be 69.3, or 69 turns per coil. The actual number of turns to achieve the desired performance has not yet been determined but for the AWG size selected, 69 turns or 138 conductors is the maximum practical limit.
The next important parameter to establish is the coil resistance. First, one must establish the MLT in the stator coil.


The MLT value is converted into turns per feet to resolve the units and the value of ohms per foot for 22 AWG is 0.162 Q.
Stator Winding Computations. Two major motor performance parameters are required to be computed in order to establish overall motor performance. They are the torque constant Kt and the phase resistance ,Rphase. From these two parameters, all motor performance can be essentially derived.
The Kt value is derived for the case of RMS torque based on a trapezoidal torque versus position profile and near-perfect commutation. There is an adjustment of 10 percent to achieve a reasonable value for RMS torque. This value can be adjusted based on actual torque waveforms if required.
The following equation computes the Kt value per phase as described.
![]()

