ABSTRACT
Ballistic gelatin is widely used as a soft tissue simulant for non-penetrating and penetrating, and the mechanical properties of gelatin are known to be highly sensitive to strain rate and temperature. Mechanical compression testing was undertaken across a range of strain rates at constant temperature to evaluate the material response. The material strength and stiffness increased with increasing strain rate, while the strain to failure was relatively constant across a wide range strain rates. The mechanical test data was implemented in two constitutive models: a quasi-linear viscoelastic model, commonly available in explicit finite element codes, and a tabulated hyperelasticity model. The implementations were verified using simulations of the experimental tests and it was found that the quasi-linear viscoelasticity model did not adequately capture the low and high strain rate response across the range of data. The tabulated hyperelasticity model was found to provide accurate representation of the material across the range of strain rates considered, and included a damage function to predict material failure.
INTRODUCTION
Ballistic gelatin powder is produced from biological materials (skin, bone and tendons) through extraction with hot water in an acidic environment for Type A gelatin (Sellier 1994). This powder is then combined with water, heated and mixed, and conditioned at 4°C for a period of 2-3 days [Jussila 2004]. Type A, 250 Bloom is the most common gelatin formulation used in ballistic testing. The two commonly used mixtures are the Fackler formulation (10%, 40C) (Fackler 1988) and the NATO formulation (20%, 100C). The 10% formulation was considered for this study since it has been shown to better represent the properties of muscle tissue compared to the 20% gelatin (Van Sligtenhorst 2004). Gelatin is known to have a density close to that of soft tissue (approximately 1060 kg/m3) (Sellier 1994) and a an elastic wave speed of approximately 1540 to 1550 m/s Van Bree (1996, 1998, 1999).
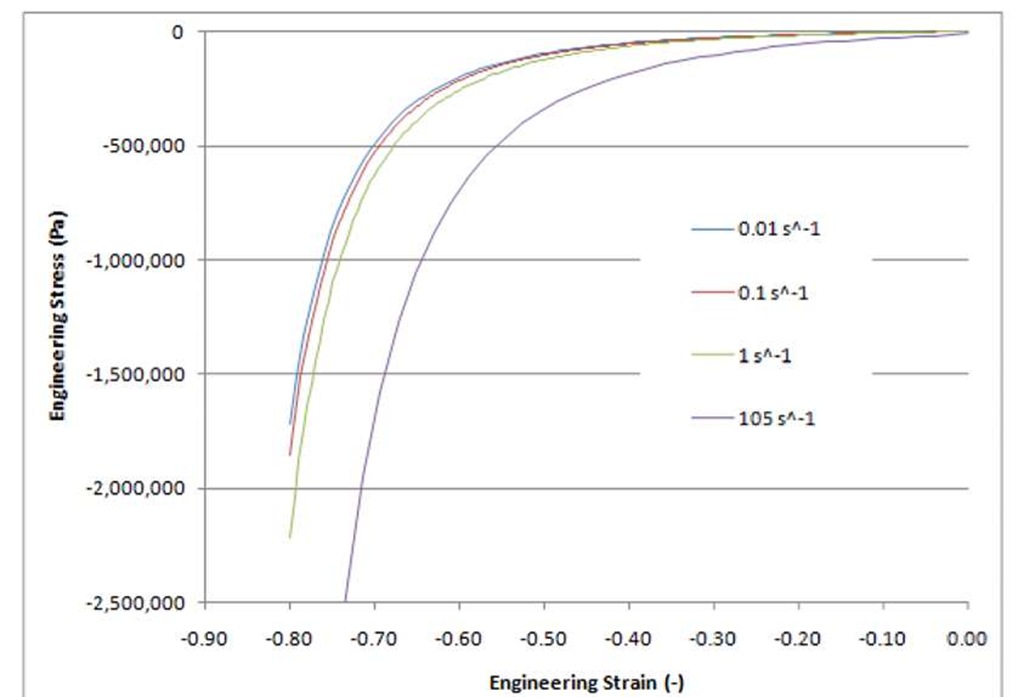
Previous studies have investigated the characterization of ballistic gelatin, and evaluation as a tissue simulant (Van Sligtenhorst 2004, Cronin 2006, Caillou 1994, Van Bree 1998, Sellier 2004, Salisbury 2009) based on mechanical properties and penetration studies. A recent study on the mechanical properties of 10% gelatin provided mechanical data at strain rates of 0.01 s-1, 0.1 s-1, and 1.0 s-1 (Figure 1) (Cronin 2010). Intermediate strain rate data, ~100 s-1 has previously been reported (Cronin 2009) and was augmented for this study with additional test data. High strain rate data on the order of 1000 s-1 (Salisbury 2009) was not considered in this study.
Figure 1: 10% Gelatin compressive mechanical properties at low and intermediate strain rates
It should be noted that all test data considered corresponds to 10% Type A, Bloom 250 Gelatin at a temperature of 4°C, which had been conditioned (aged) for approximately 72 hours. The actual conditioning time varied, and the gelatin was determined acceptable using the standard BB impact test (Jussila 2004). It has been shown that insufficient conditioning time or temperatures exceeding 4°C can significantly change the measured mechanical properties (Cronin 2010).
METHODS
The material data was recorded in terms of applied compressive force and deformation and was converted to engineering stress and strain based on the initial sample dimensions. The true stress and strain, required for constitutive modeling purposes, were calculated from equations 1 and 2 assuming constancy of volume of the samples. This is a reasonable assumption up to the initiation of material damage.
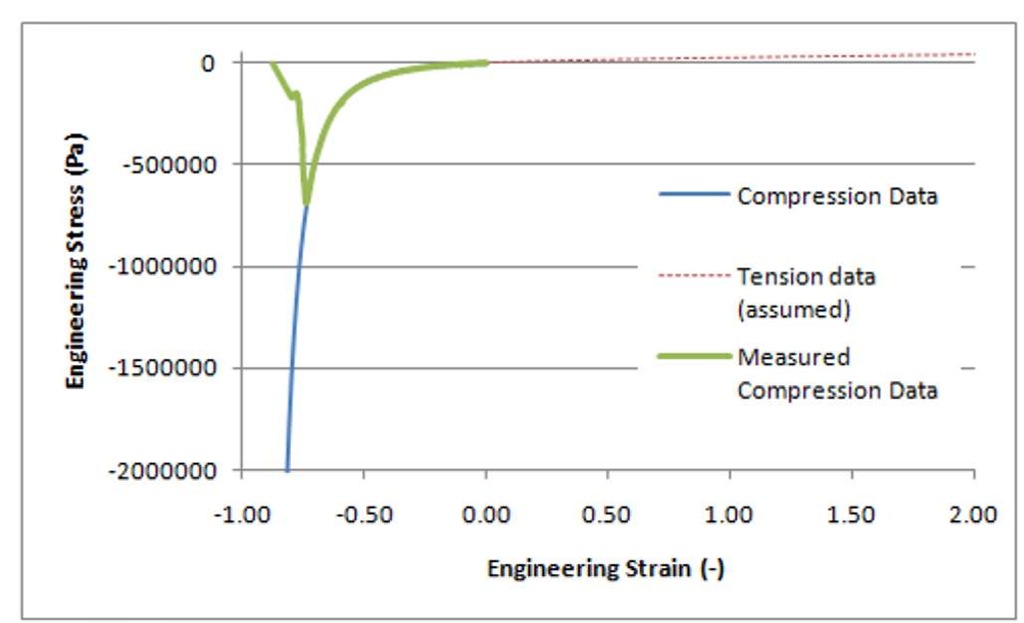
Based on the test data (Figure 1) it was apparent that the mechanical properties of ballistic gelatin were sensitive to deformation rate and this should be considered in any constitutive model. Available constitutive models for viscoelastic materials can be generally classified as linear, quasi-linear, and non-linear viscoelastic. The selection of a model was guided by the material response, and by commonly available models in numerical codes since the goal of this work was to use the properties and models to evaluate gelatin response to impact conditions. As a frame of reference, unpublished relaxation test data on 10% gelatin has shown that under relatively low strains (~20% engineering strain), 10% gelatin samples continue to relax for durations exceeding 15 hours. This suggests that the stress strain curve at 0.01 s-1 (Figure 1) does not represent the instantaneous elastic response or fully relaxed behavior of gelatin. However, this rate is relatively low for impact phenomena and was used to represent the fully relaxed behavior in this study. It should be noted that most constitutive models require complete definition of the material response across the range of strain rates and strains considered, and in the case of a inputting a discrete curve in a model, care must be taken to ensure the curve is defined across the entire range of anticipated strains. For this study, the instantaneous response curve was extended beyond the test data using a hyperelastic curve fit, and the tensile properties were determined by assuming symmetric behavior in terms of true stress and strain. This curve is shown in Figure 2, along with the original compression test data.
The quasi-linear viscoelastic model as proposed by Fung (1993) for soft tissues and similar materials is widely implemented in numerical modeling codes and was evaluated for this study. Specifically, the implementation in the explicit finite element code LS-Dyna (LSTC, 2009) was investigated. This model requires a representation of the instantaneous elastic response of the material, typically expressed in terms of a hyperelastic stress (aH(e)), and predicts strain rates through the addition of a viscoelastic stress component (aV(e,t)) based on the convolution integral as shown in equations 3a, b and c.
The mechanical properties at a strain rate of 0.01 s-1 were selected to provide the instantaneous elastic response of the gelatin material. It should be emphasized that this selection is somewhat arbitrary; typically a strain rate below which response will not be evaluated is selected to provide this response. It was found that commonly available hyperelastic models (Mooney, Ogden) could represent the stress-strain curve at 0.01 s-1 with r2 values exceeding 0.999. The specific implementation of the quasi-linear viscoelastic model allowed for an effective stress versus strain expressed as a polynomial, or actual test data to be implemented directly. For the purposes of this study, the properties were implemented directly using the tension and compression response shown in Figure 2.
Figure 2: Instantaneous elastic response data plotted with original test data
A second constitutive model using tabulated stress-strain and strain rate data (Kolling et al. 2007, LSTC 2009) was investigated. This model uses the same concept of an instantaneous hyperelastic response (shown in Figure 2) and incorporates rate effects through the inclusion of actual stress-strain and strain rate data. Similar to the quasi-linear viscoelastic model, the compression test data was extended to strains beyond the material failure strain, and assumed symmetric in tension based on the true stress-strain data. This data was included in the material model, and material failure was addressed through a damage approach, described below.
Following model fitting, the data was implemented in an explicit finite element code (LS-Dyna, LSTC 2009) and evaluated using single element test cases, and multiple element test cases. The element size for the simulations was on the order of 1mm, a typical value used to simulate ballistic gelatin in impact scenarios (Cronin, 2009).
Both constitutive models considered incorporate a damage-based failure model that could be used to predict the onset of damage and final failure of the material. In this study, the form of the damage model used was based on the first invariant of stretch (equation 4). The full damage model allows for dependence on the square of the first invariant and the second invariant, but only the first term could be justified based on the available test data. The variable K corresponds to 100% damage (D). A second parameter (h) determines the initiation of damage in the material (equation 5).
Figure 3: Finite element models – 1 mm single element [L] and 25 mm diameter cylinder [R] (not to scale)
RESULTS AND DISCUSSION
The quasi-linear viscoelastic model was evaluated relative to the data presented in Figure 1. Although an adequate fit could be achieved with the quasi-linear viscoelastic model for strain rates of 0.1 s-1 (r2 = 0.993) and 1.0 s-1 (r2 = 0.980), the fit for the intermediate rate data (105 s-1, r2=0.885) was not satisfactory. Also, the general shape of the curve was not in good agreement with the experimental data. This was verified using single element simulations, but was not pursued further. It is anticipated that this modeling approach would not be able to accurately represent data at higher strain rates.
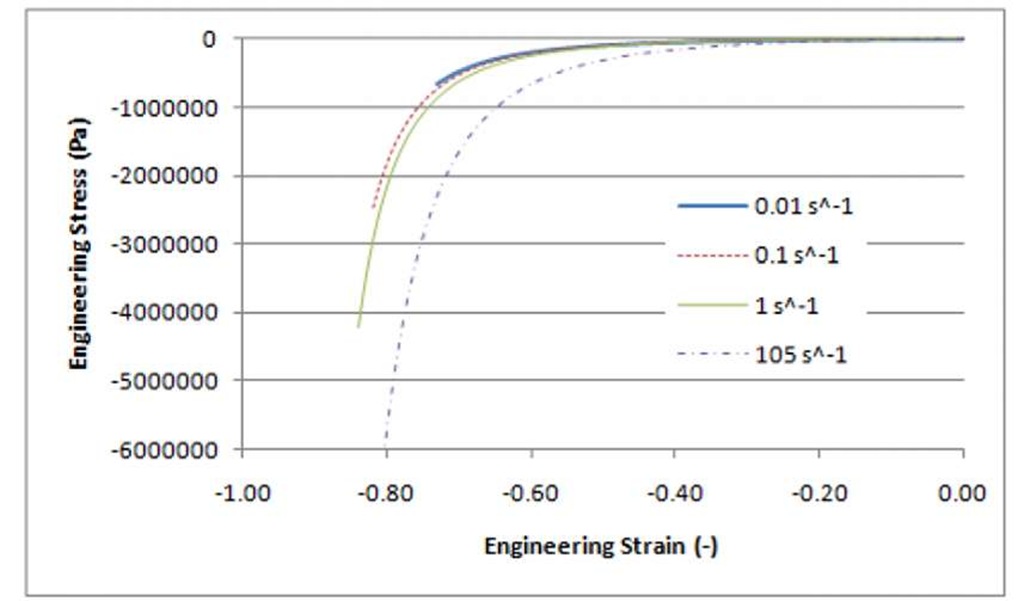
The tabulated hyperelasticity model was evaluated using single element test cases in uniaxial compression, and found to reproduce the material data accurately across the range of strains and strain rates considered. Simulations on a multi-element cylindrical sample (Figure 3) were also undertaken and found to produce consistent results, although some oscillation occurred early in the simulation as the sample achieved equilibrium, and a small radial inertial effect was noted.
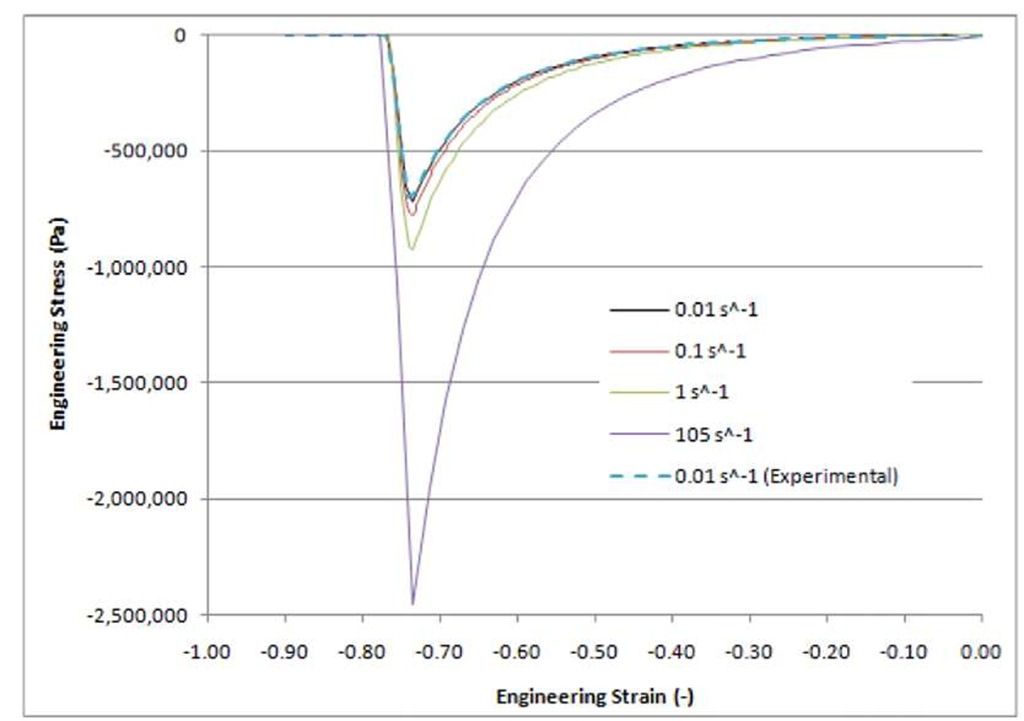
The damage model was fit to the experimental test data presented in Figure 2 using a spreadsheet calculation (K=5.7 and h=0.2) and incorporated in the material model. The compression test at a strain rate of 0.01 s-1 was simulated and found to be in good agreement with the experimental data (Figure 5).
Figure 4: Tabulated hyperelasticity model predictions
Figure 5: Damage model predictions compared to experimental test data
CONCLUSIONS
The mechanical properties for 10% Type A, 250 Bloom ballistic gelatin were investigated using two different constitutive models. A quasi-linear viscoelastic model, commonly available in finite element codes, was found to provide reasonable predictions for the low strain rate data, but did not accurately predict the intermediate strain rate data in terms of stress magnitude or the shape of the curve. A tabulated hyperelasticity model, based on the actual stress-strain and strain rate curves from the experimental tests, was found to accurately predict the material response across the range of strains and strain rates considered. In addition, the available material damage model was capable of predicting material damage and ultimate failure. Future work will investigate alternate hyper-viscoelastic models. The benefit of this class of material model is the capability to predict material response without the need or bias for specific test data across the range of strains and strain rates.
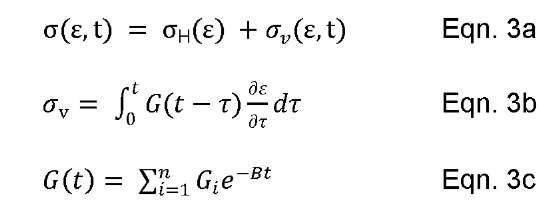
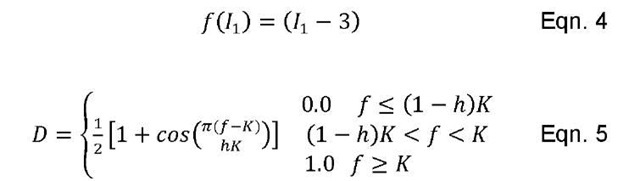
![Finite element models - 1 mm single element [L] and 25 mm diameter cylinder [R] (not to scale) Finite element models - 1 mm single element [L] and 25 mm diameter cylinder [R] (not to scale)](http://what-when-how.com/wp-content/uploads/2011/07/tmp1961_thumb_thumb.jpg)