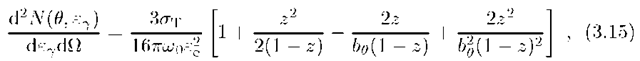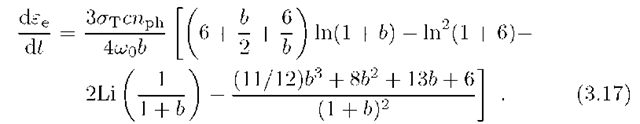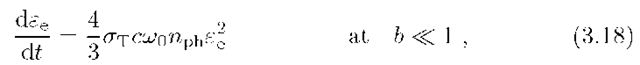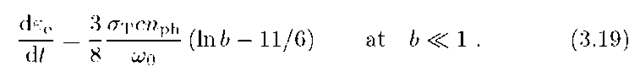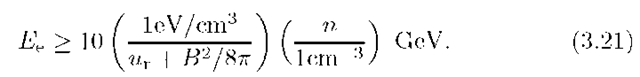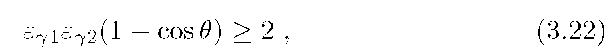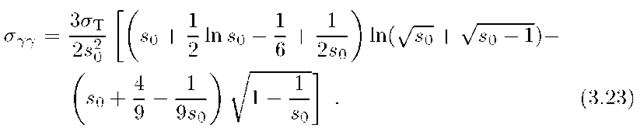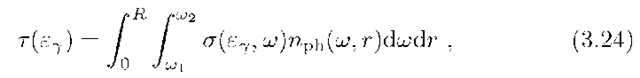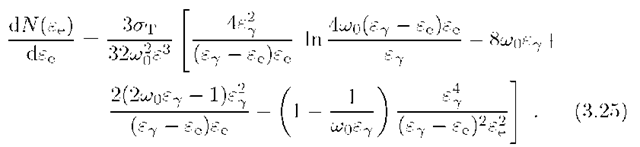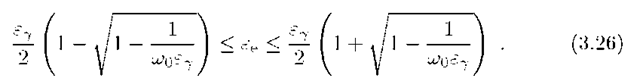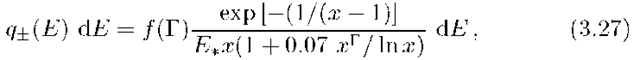The interaction of relativistic electrons with radiation fields through inverse Compton scattering provides one of the principal Y-ray production processes in astrophysics. It works effectively almost everywhere, from compact objects like pulsars and AGN to extended sources like supernova remnants and clusters of galaxies. Because of the universal presence of the 2.7 K CMBR, as well as low gas densities and low magnetic fields, inverse Compton scattering proceeds with very high efficiency in the intergalactic medium over the entire Y-ray domain. Since the Compton cooling time decreases linearly with energy, the process becomes especially effective at very high energies.
The electron-positron pair production in photon-photon collisions is tightly coupled with inverse Compton scattering. First of all, it is an absorption process that prevents the escape of energetic Y-rays from compact objects, and determines the "Y-ray horizon" of the Universe. At the same time, in an environment where the radiation pressure dominates over the magnetic field pressure, the photon-photon pair production and the inverse Compton scattering "work" together supporting the effective transport of high energy radiation via electromagnetic "Klein-Nishina" cascades.
Although the inverse Compton scattering of protons is suppressed by a factor of
very high energy protons effectively interact with the ambient photon fields through electron-positron pair-production and photomeson processes. While in the first process Y-rays are produced indirectly, via inverse Compton scattering of the secondary electrons, photo-meson reactions result in the direct production of
and their subsequent decay to Y-rays. Typically, at extremely high energies these interactions proceed effectively both in compact objects and large scale structures.
Inverse Compton scattering
The derivation of the cross-section for Compton scattering with given four-vector momenta of the electron and photon can be found in Akhiezer and Berestetskii (1965). The basic expressions of the inverse Compton scattering (i.e. when the energy of the electron significantly exceeds the energy of the target photon) have been comprehensively analysed by Jones (1968), Blumenthal and Gould (1970) and Coppi and Blandford (1990) for the case of isotropically distributed photons and electrons.
The angle-averaged total cross-section of inverse Compton scattering depends only on the product of the energies of the interacting electron e and photon
(where all energies are in units of
In the nonrelativistic regime
it approaches the classical (Thomson) cross- section
while in the ultrarelativistic regime
it decreases with
With an accuracy of better than 10 per cent in a very broad range of k0, the cross-section can be represented in the following simple form (Coppi and Blandford, 1990)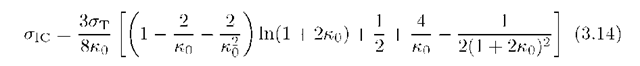 
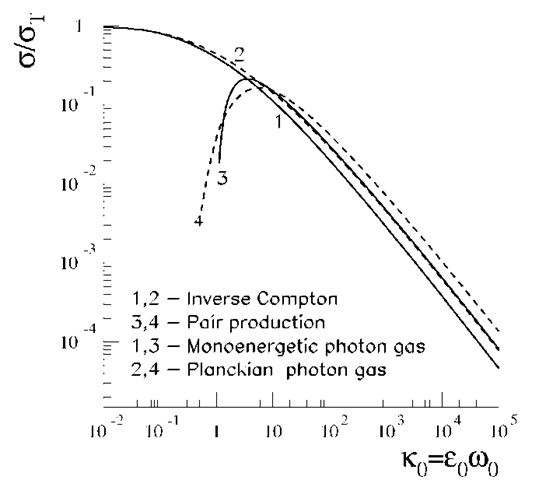
The total cross-section of Compton scattering as a function of k0 is shown in Fig. 3.4.
The energy distribution of up-scattered Y-rays is determined by the differential cross-section of the process. Assuming that a monoenergetic beam of low energy photons w0 penetrates an isotropic and homogeneous region filled with relativistic electrons of energy ee, the spectrum of radiation scattered at the angle 0 relative to the initial photon beam is written as
where
The energy of the high energy Y-ray photon e7 varies in the limits
In the case of isotropically distributed electrons and photons, the integration of Eq.(3.15) over the angle 0 gives (Jones, 1968, Blumenthal and Gould, 1970)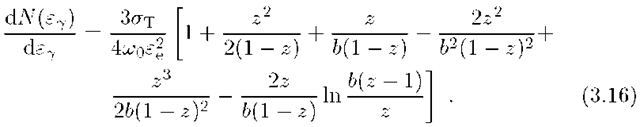 
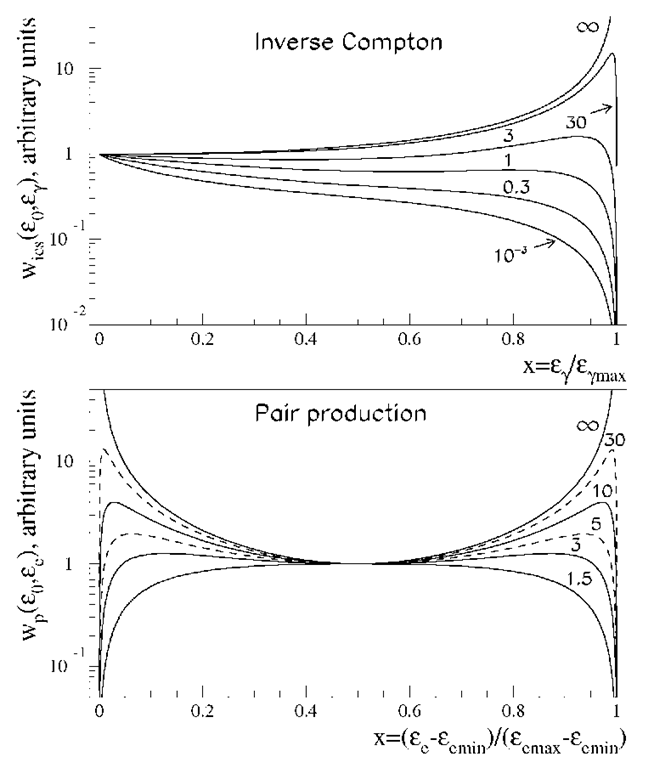
The differential energy spectra of Y-rays for several fixed values of k0 are shown in Fig. 3.5. In the deep Klein-Nishina regime
the spectrum grows sharply towards the maximum at
This implies that in this regime just one interaction is sufficient to transfer a substantial fraction of the electron energy to the upscattered photon (see also Table 3.1).
Fig. 3.4 Total cross-sections of inverse Compton scattering and photon-photon pair production in isotropic radiation fields. Two spectral distributions for the ambient photon gas are assumed: (i) monoenergetic with energy wo (curves 1 and 3), and (ii) Planckian with the same mean photon energy
(curves 2 and 4).
In the Thomson regime
the average energy of the upscattered photon is
thus only a fraction
of the primary electron energy is released in the upscattered photon.
For a power-law distribution of electrons,
the resulting Y-ray spectrum in the nonrelativistic regime
has a power- law form with photon index
(Ginzburg and Syrovatskii, 1964). In the ultrarelativistic
regime the Y-ray spectrum is no ticeably steeper,
with
(Blumenthal and Gould, 1970). Several useful analytical approximations for Y-ray spectra over a broad energy interval, including these two regimes and the Klein-Nishina transition region
can be found in Atoyan (1981c) and Coppi and Blandford (1990).
Fig. 3.5 Differential spectra of Y-rays from inverse Compton scattering (upper panel) and electrons from photon-photon pair production (bottom panel) in an isotropic and mono-energetic photon field. The parameters
are defined as
The same values of the parameters
are indicated by the curves.
The spectral features of the inverse Compton radiation in power-law target photon fields have been studied by Zdziarski (1988)
Table 3.1 The mean fraction of primary energy
transferred to the secondary photon in the inverse Compton scattering (ics) and the synchrotron radiation (syn) processes for different values of the parameters
respectively.
 |
0.01 |
0.1 |
1 |
10′2 |
104 |
106 |
 |
0.014 |
0.099 |
0.358 |
0.760 |
0.867 |
0.910 |
 |
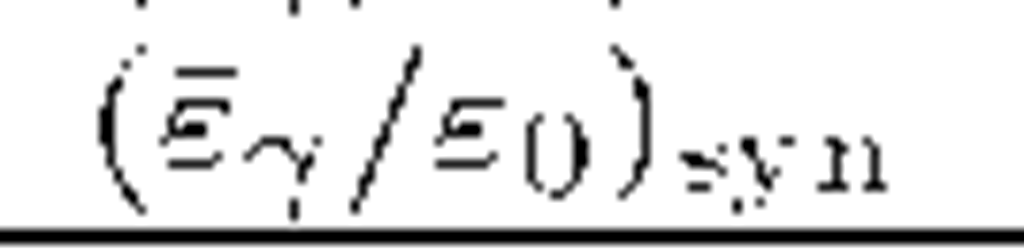0.44 • 10-2 |
0.033 |
0.118 |
0.241 |
0.250 |
0.250 |
The energy-loss rate of relativistic electrons in a monoenergetic field of photons with energy w0 and number density nph is given by the following equation.
where
In the Thomson and Klein-Nishina regimes Eq.(3.17) reduces to the well known expressions (e.g. Blumenthal and Gould, 1970)
and
The energy losses in these two regimes have quite a different dependence on the electron energy. While in the Thomson regime the loss rate is proportional to e^, in the Klein-Nishina regime it is almost energy independent. This implies that in the first case the steady-state electron spectrum becomes steeper, whereas the Compton losses in the Klein-Nishina regime make the electron spectrum harder.
For calculations of electron energy losses in radiation fields with more realistic distributions one should integrate Eqs.(3.17)-(3.19) over w0. It is interesting to note that in the Thomson regime the energy-loss rate does not depend on the spectral distribution of target photons, but depends only on the total energy density of radiation ur. Correspondingly, the cooling time of electrons due to Thomson scattering is given by
where the radiation energy density
and the electron energy
are expressed in units of
respectively. Note that the same equation describes the synchrotron energy losses if we replace
by the magnetic field energy density
The comparison of Eq.(3.20) with the bremsstrahlung cooling time given by Eq.(3.4) shows that Compton and synchrotron losses dominate over the bremsstrahlung cooling, if
Photon-photon pair production
Photon-photon pair production is the inverse process to pair annihilation. Therefore the differential cross-section is identical to the pair annihilation cross-section, except for a different phase-space volume. In the relativistic regime this process is quite similar also to inverse Compton scattering. However, unlike the pair annihilation and Compton scattering, the photon-photon pair production has a strict kinematic threshold given by
where
are the energies of two photons in units of
colliding at an angle 0 (in the laboratory frame).
The large cross-section makes the photon-photon pair production one of the most relevant elementary processes in high energy astrophysics. The role of this process in the context of intergalactic absorption of Y-rays was first pointed out by Nikishov (1962). Bonometto and Rees (1971) were first who emphasised the importance of this process in dense radiation fields of compact objects.
Several convenient approximations for the total cross-section of this process in the isotropic radiation field have been proposed by Gould and Schreder (1967), Coppi and Blandford (1990). With an accuracy of better than 3 per cent, the total cross-section in the monoenergetic isotropic photon field can be represented in the following analytical form
The total cross-sections of inverse Compton scattering and pair production in an isotropic monoenergetic photon field of energy
are shown in Fig. 3.4 (curves 1 and 3, respectively). Both cross sections depend only on the product of the primary
and target photon
energies,
While as
the inverse Compton cross- section approaches the Thomson cross-section,
the pair production cross-section approaches zero,
For
the two cross-sections are quite similar and decrease with k0 and
The pair-
production cross-section has a maximum at the level of
achieved at
The parameter that characterises Y-ray absorption at photon-photon interactions in a source of size R is the so-called optical depth
where
describes the spectral and spatial distribution of the target photon field in the source. For a homogeneous source with a narrow spectral distribution of photons, for order of magnitude estimates one can use the approximation
where
is the average target photon energy. However, generally one has to be careful with this type of estimate, especially at low energies; while this approximation implies a completely transparent source
in fact non-negligible absorption can take place at low energies. For example, for a Planckian distribution of target photons, the optical depth t cannot be disregarded at energies
because of interactions with photons from the Wien tail region (see Fig. 3.4). Very useful approximations for the optical depth of Y-rays in a Planckian photon gas can be found in Gould and Schreder (1967).
Because of narrowness of the pair-production cross-section, for a large class of broad band target photon energy distributions
the optical depth at given Y-ray energy
is essentially determined by a relatively narrow band of target photons with energy centered on
(Her-terich, 1974). Therefore, the optical depth can be written in the form
where the normalization factor n depends on the spectral shape of the background radiation. For a power-law target photon spectrum,
the parameter n is calculated analytically,
(Svensson, 1987).
The energy spectrum of electrons produced at photon-photon pair production has been studied by Zdziarski and Light-man (1985), Coppi and Blandford (1990) and Bottcher and Schlickeiser (1997). For a low-energy monoenergetic photon field
, and correspondingly
the spectrum of electron-positron pairs can be rep
resented, with an accuracy of better than a few per cent:
The kinematic range of variation of
is
The differential energy spectra of Y-rays for several fixed values of the parameters
are shown in Fig. 3.5. The spectra are symmetric around the point
Although the average energy of the secondary electrons is
for very large s0 the interaction has a catastrophic character – the major fraction of the energy of the primary Y-ray photon is transferred to the leading electron. This fraction exceeds 0.5 and asymptotically approaches 1 (see Table 3.2).
For calculation of electron spectra produced in radiation fields by Y-rays with more realistic spectral distributions,
one should integrate the product of spectrum given by Eq.(3.25) and
over a broad primary
Y-ray energy interval. For a power-law spectrum of Y-rays,
the spectrum of secondary pairs can be approximated, with an accuracy of better than 20 per cent:
where
and
(two electrons per interaction). Starting from the minimum (allowed by kinematics) energy at
the electron spectrum sharply rises achieving its maximum at
and then at
it behaves as
Table 3.2 The mean fraction of energy of the primary 7-ray photon transferred to the leading secondary electron at electron-positron pair production in a mono-energetic radiation field (rad) and in the magnetic field (B) for different values of the parameters
respectively.
 |
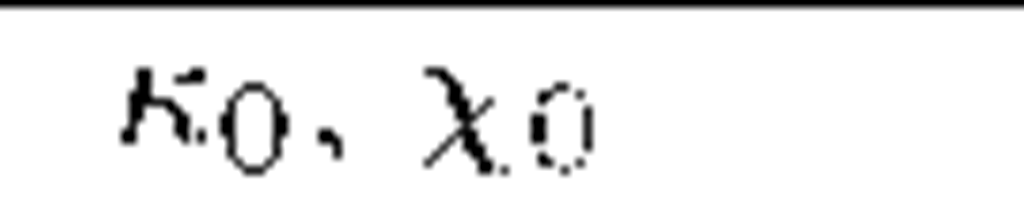1 |
3 |
10 |
W’2 |
104 |
10b |
 |
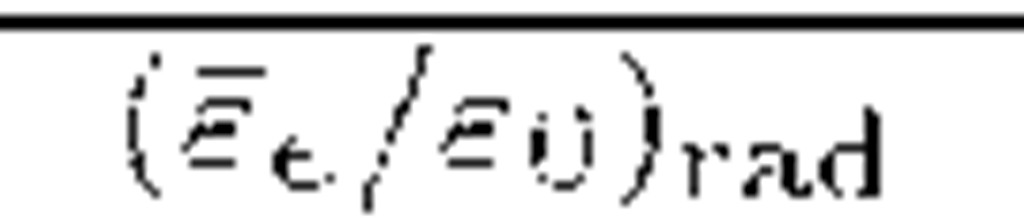0.500 |
0.701 |
0.797 |
0.891 |
0.948 |
0.966 |
 |
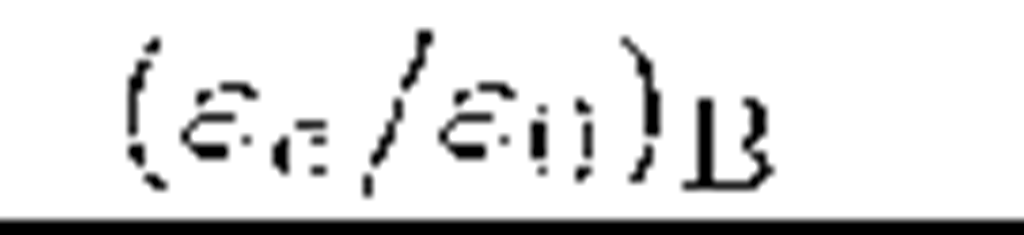0.634 |
0.693 |
0.746 |
0.782 |
0.824 |
0.825 |
Two pairs of coupled processes – inverse Compton scattering and photon-photon pair production – determine the basic features of interactions of electrons and Y-rays in the radiation dominated environments. At extremely high energies higher order QED processes may compete with these basic channels. Namely, when the product of the energies of colliding cascade particles (electrons or photons) E and the background photons w significantly exceed
the processes
(Brown et al., 1973) and
(Mastichiadis, 1991; Dermer and Schlickeiser, 1991) dominate over single
pair production and Compton scattering, respectively. For example, in the 2.7 K CMBR the first process stops the linear increase of the mean free path of the highest energy Y-rays around 1021 eV, and puts a robust limit on the mean free path of Y-rays of about 100 Mpc. Analogously, above 1020 eV the second process becomes more important than the conventional inverse Compton scattering. Because the 
channels result in production of 2 additional electrons, they substantially change the character of interactions. Note, however, that an effective realization of these processes is possible only under very specific conditions with an extremely low magnetic field and narrow energy distribution of the background photons.
