The previous section shows how network coding combines raw bits or packets at the network layer to improve rates. More generally, cooperative coding combines symbols at the physical and higher layers to produce new symbols. We consider several types of cooperative coding strategies, including
(1) amplify-and-forward (AF)
(2) classic multi-hop
(3) compress-and-forward (CF)
(4) decode-and-forward (DF)
(5) multipath decode-and-forward (MDF)
(6) DF or MDF with network coding.
Mode coding seems related to sending "bits through queues" [7].
The above strategies can be used for both wireline and wireless networks and they require progressively more coordination. For example, consider a RC. AF and classic multi-hop do not necessarily require changes at the source or destination nodes, e.g., for multi-hop the relay can behave as if it is the destination or the source. CF does not necessarily require changes at the source but it does require some extra knowledge about the link capacities. DF requires changes at both the source and destination, and MDF requires additional changes at higher layers of the protocol stack. DF or MDF with network coding require even more changes at higher layers. Some of these issues are discussed in the sections below. However, we begin by specifying the models used in this section.
Idealized Wireless Models
In this section, we will describe and compare wireless strategies by using two idealizations:
• we consider full-duplex radios, i.e., devices that can transmit and listen at the same time in the same frequency band;
• if the channels are time-varying, we assume per-link channel state information is available at the receiver but not at the transmitter (CSIR, No CSIT, see Section 3.4).
We defer consideration of duplexing constraints to Section 4.3. Note that full-duplex operation is often not possible due to large difference in transmit and receive power2 (see Section 3.3). However, full-duplex models have didactic utility in that their capacities can sometimes be written in closed-form. Furthermore, the information theory developed for the full-duplex models applies directly to wireline problems and, perhaps surprisingly, to half-duplex models as well [103, 106].
The basic cooperative model is the relay channel shown in Figure 3.5 [33, 106]. In our derivations, we consider a general geometry shown in Figure 4.8(a) with nodes u and v at distance duv. For numerical evaluations, we employ the linear geometry shown in Figure 4.8(b), where the source and destination nodes are a distance d13 = 1 apart, and the relay is a distance d12 = |d| to the right of the source, and a distance d23 = |1 — d| to the left of the destination.
2 Some devices can operate in full-duplex mode with good echo cancellation.
Fig. 4.8 Relay channel geometries: (a) In general, nodes u and v are separated by distance duv; (b) In the linear case, the source-destination distance is dl3 = 1, the source-relay distance is dl2 = |d| and the relay-destination distance is (I23 = |1 — d|.
A negative d means that the relay is to the left of the source. We remark that we are here considering distances duv that are less than one, in seeming disregard of our claim in Section. 2.2.1 that we are interested in long-range communication where the model (2.3) is accurate. However, we are in effect normalizing the source-destination distance to be unity, and including long-range attenuation in the power constraints. For example, when we later find in Section 4.2.6 that DF achieves capacity when the relay is near the source, the distance need not be less than one but rather shows where the relay must be relative to the source and destination.
We consider channels that exhibit one of three kinds of fading: (1) no fading; (2) fast uniform-phase fading; and (3) fast Rayleigh fading (see Section 3.2). That is, for every clock tick we have the complex channels (see (3.3a) and (3.3b))
For no fading, the Huv are constants. For uniform-phase fading, the Huv are independent and uniform over![]() For Rayleigh fading, the Huv are independent and Gaussian with zero mean and unit variance.
For Rayleigh fading, the Huv are independent and Gaussian with zero mean and unit variance.
For CSIR, we assume that all nodes know the distances duv, but for uniform-phase and Rayleigh fading Huv is known only to node v, i.e., only the relay knows H12, and only the destination knows H13 and H23. As in Section 3.4, we model this by augmenting Y2 and Y3 to become the vectors [Y2 H12] and [Y3 H13 H23], respectively. As we will see, channels whose phase varies rapidly exhibit a special property that we exploit to derive capacity theorems. Furthermore, we shall later see that making the relay half-duplex brings both complications and simplifications to our theory and strategies.
Amplify-and-Forward
Amplify-and-forward has the relay transmit
where the a2,j, i = 1,2,…,n, are chosen to satisfy the relay’s power constraint [59, 111, 161]. More generally, the relay might transmit some function of a small number of the past received symbols, e.g.,
where the a2 i, i = 1,2,…, n, are row vectors chosen to satisfy the relay’s power constraint. Consider (4.6) where a2,j = a for all i so that we have (see (4.5b))
To satisfy the power constraint, we require
Observe that, without fading, (4.9) is an AWGN channel with unit-memory intersymbol interference (ISI). In general, one should therefore perform a waterfilling optimization of the spectrum of X^ (cf. Section 2.2.5, Section 3.4, and [106, Sec. VII.B]). The result is shown in
Fig. 4.9 Rates for a full-duplex relay, Pl/N = P2/N = 10, Huv = 1 for all (u, v), and a = 2.
Figure 4.9 for the linear geometry of Figure 4.8(b) as the curve labeled "AF," where P1 /N = P2/N = 10, Huv = 1 for all (u,v) and a = 2. The relay-off rate is simply log2(11). The curve labeled "upper bound" is the cut-set bound (3.33). The other curves are based on the CF and DF strategies developed further below. Note that AF always performs as well as using no relay by choosing a = 0. Note also that increasing a from 0 increases the destination’s ISI and noise power. The relay should thus not always transmit with maximum power.
The AF rates in Figure 4.9 are often significantly worse than the rates achieved by other strategies. However, AF can sometimes perform very well [59]. For example, consider the RC with T relays3 shown in Figure 4.10. Suppose every relay u, u = 2,3,… ,T + 1, has
Fig. 4.10 A multi-relay channel and geometry.
and E[|Zu|2] = N. If 0 < d < 1, Huv = 1 for all (u,v), and every relay uses AF as in (4.6) with au,j = a, then we have
and the T-relay version of (4.9) is
Note that there is no channel from node 1 to node T + 2. Equation (4.13) thus defines an AWGN channel with SNR
But the cut bound (3.24) in Section 3.7.1 with S = {1,2,…,T + 1} gives
We thus have
so that C grows as klog2(T) with T, where 1 < k < 2. Furthermore, AF achieves this scaling law up to a constant factor.
The above scenario permits the total system power to grow linearly with T. Instead, one might require P = Psum/T for some constant Psum. We choose (see (4.10))
Inserting (4.17) into (4.14) and (4.15), we find that
Now C grows as log2(T) with T and AF achieves this scaling law up to a rate offset. We remark that both the scaling laws (4.16) and (4.18) require coherent combining of signals at the destination.
Classic Multi-Hop
Classic multi-hop has the source transmitting its message W to the relay in one-time slot, and then the relay forwarding W to the destination in a second-time slot. This scheme can be used with both full-duplex and half-duplex relays. Suppose we assign the time fractions t to the first hop and f = 1 — t to the second hop. For constant H12 and H23, we achieve
However, even after optimizing t one always performs worse than using no relay for any d in Figure 4.9. This happens because a = 2 is too small to make multi-hopping useful. We will see later that multi-hop can work well for half-duplex relays and larger a.
Compress-and-Forward
We continue to consider the no-fading case for simplicity. CF is a block-transmission strategy with the block structure shown in Figure 4.11 [33]. There are three codebooks: x1(-), x2(-), and a quantization codebook y2(-). The source transmits x1(wb) indexed by a new message wb in every block b.
Fig. 4.11 A CF strategy for a full-duplex relay.
The relay observes![]() in block b and chooses its next codeword as follows:
in block b and chooses its next codeword as follows:![]() is quantized to
is quantized to![]() and the index sb chooses the codeword
and the index sb chooses the codeword![]() The destination first decodes sb using
The destination first decodes sb using![]() and then decodes wb by using
and then decodes wb by using![]() and
and ![]() For the last block, the source transmits a default codeword
For the last block, the source transmits a default codeword![]() Consider, for example, the following relay encoding in block b. After canceling the effect of
Consider, for example, the following relay encoding in block b. After canceling the effect of![]() the relay uses a vector quantizer to map
the relay uses a vector quantizer to map![]() so that the average distortion (using some per-letter distortion function) between these two vectors is at most D. Shannon’s rate-distortion theory [34, Ch. 13] tells us that the rate of the codebook
so that the average distortion (using some per-letter distortion function) between these two vectors is at most D. Shannon’s rate-distortion theory [34, Ch. 13] tells us that the rate of the codebook![]() need to be at most
need to be at most ![tmp8-152_thumb[2][2] tmp8-152_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/07/tmp8152_thumb22_thumb.jpg)
The relay can transmit sb reliably to the destination in block b +1 via x2(sb) as long as
In fact, one can improve the rate specified by (4.20)-(4.22) by using a more sophisticated vector quantizer and destination decoder [33].
The idea is that the relay transmits a hash![]() of the string sb-1
of the string sb-1
in block b, i.e., the relay sends![]() and finds a quantization vector
and finds a quantization vector![]() in block b. The hashing is also known as binning and
in block b. The hashing is also known as binning and![]() is called a bin index. The result is that any rate R satisfying
is called a bin index. The result is that any rate R satisfying
is achievable where the joint probability distribution of the random variables factors as
As done in (4.24), we will write PX(x) as P(x) if the argument of P(■) is a lower-case version of the random variable symbol. Note that the only change from (4.20)-(4.22) is that the quantization codebook has a lower rate than in (4.20), namely![]() The factorization (4.24) reflects that the
The factorization (4.24) reflects that the![]() and
and![]() codewords in block b are chosen independently, and that
codewords in block b are chosen independently, and that![]() is chosen as a function
is chosen as a function
A few remarks are in order. First, note that the rate (4.23) is the rate of a point-to-point channel where the receiver has a vector output [Y2 Y3]. The CF strategy is thus closely related to multi-antenna reception (see [57, 106]). In fact, if the relay-to-destination channel capacity is very large (say, if the relay is close to the destination) then the quantization code book can be very large and Y2 is "almost" Y2. The CF strategy will then work well. Second, it is interesting that the maximization of R in (4.23) turns out to be equivalent to the maximization of (see [45])
subject to (4.24). Third, one can time-share several modes of operation in (4.23) and (4.24), i.e., the source and relay use the respective distributions![]() for a fraction P(q) of the time, where q represents one of a finite number of modes. Suppose that the source
for a fraction P(q) of the time, where q represents one of a finite number of modes. Suppose that the source
and relay cycle through these modes several times. The relay can then collect its quantization bits over all modes, and transmit them at the average rate I(X2; Y3|Q) to the destination. The result is that any rate satisfying
is achievable where the joint probability distribution of the random variables factors as
The above rate sometimes improves the basic CF rate in (4.23) [45]. In fact, one can similarly add a time-sharing random variable Q to all the strategies in this topic, but we will not consider this explicitly. Finally, note that the relay needs to know the statistics of Y3 to compute its compression and channel coding rates in (4.23b). The relay might thus need to know![]()
As a numerical example, suppose there is no fading. We choose X1 and X2 to be the usual Gaussian distributions, and![]() where
where![]() are independent, Gaussian random variables with variance
are independent, Gaussian random variables with variance![]() (this choice of
(this choice of![]() is not necessarily optimal). The resulting information rates are
is not necessarily optimal). The resulting information rates are
The choice
thus satisfies (4.23b) with equality (see also [57] and [79, Sec. 3.2]). Consider again the case P1/N = P2/N = 10, Huv = 1 for all (u,v), a = 2, and the linear geometry of Figure 4.8(b). The resulting CF rates are shown in Figure 4.9 as the curve labeled "CF." Observe that CF performs well when the relay is close to the destination (d w 1) and even meets the cut-set bound (3.33) when d = 1. Furthermore, CF significantly outperforms AF everywhere.









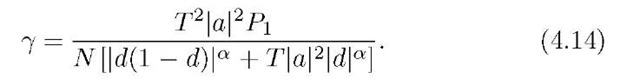






![tmp8-153_thumb[2][2] tmp8-153_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/07/tmp8153_thumb22_thumb.jpg)
![tmp8-171_thumb[2][2] tmp8-171_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/07/tmp8171_thumb22_thumb.png)
![tmp8-186_thumb[2][2] tmp8-186_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/07/tmp8186_thumb22_thumb.png)
![tmp8-198_thumb[2][2] tmp8-198_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/07/tmp8198_thumb22_thumb.png)
![tmp8-199_thumb[2][2] tmp8-199_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/07/tmp8199_thumb22_thumb.jpg)
