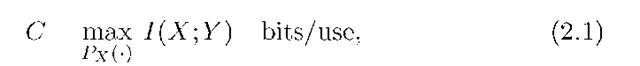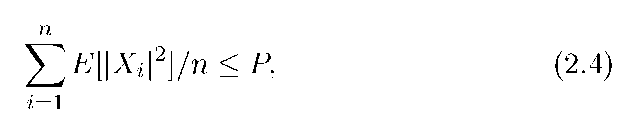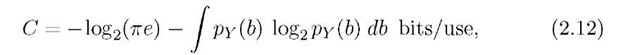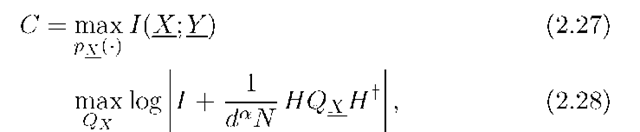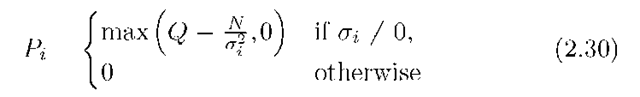We review basic concepts of communication theory. This theory is useful for all network layers, but in particular for the PHY and application layers where source and/or channel coding are used. The following sections also introduce notation that we use throughout the document.
Information Theory
Information theory began as the mathematics of communications for one source and one channel [164]. Consider Figure 2.2 and suppose the source puts out a message W that consists of B independent and uniformly distributed bits. Let X and Y be random variables representing the channel input and output with alphabets X and Y, respectively. A discrete memoryless channel (DMC) is a conditional probability distribution PY|X, where X and Y are discrete and finite.1 The encoder transmits a string Xn = X1 ,X2,.. .,Xn that is a function of W.
Fig. 2.2 Communications model.
1 The theory generalizes to continuous random variables in natural ways.
The decoder sees Yn = Y1,Y2,…,Yn and puts out a message estimate W that is a function of Yn.
The capacity is the maximum rate R = B/n bits per channel use for which, for sufficiently large n, there exists a W-to-Xn mapping (an encoder) and a Yn-to-W mapping (a decoder) so that the error probability Pr[W = W] can be made as close to 0 as desired (but not necessarily exactly 0). It is a remarkable fact that such a capacity exists. Perhaps just as remarkably, the capacity is given by the compact formula
where
is the mutual information between X and Y. The formula (2.1) is universal in the sense that it gives the capacity for any DMC. Furthermore, the capacity proof is based on a random code construction method that is useful for many other communication problems [34, 35].
Similarly, consider the additive white Gaussian noise (AWGN) channel
with power constraint
where X and Z are real random variables; Z has variance N; h, d, and a are real numbers; and E denotes expectation. The variables h and d represent channel gains and distances between the encoder and decoder, respectively, and a is an attenuation exponent (e.g., a = 2 for free-space propagation). The model (2.3) is not accurate for small d. For example, as d approaches zero, we have the physically untenable result that the received power exceeds the transmitted power. However, we will be mainly interested in "long-range" communication where (2.3) is a reasonable model for distance-dependent attenuation. The capacity formula (2.1) generalizes in a straightforward way to AWGN channels, namely
where pXY(a, b) is the joint probability density of X and Y (if X is discrete, then replace pX(a) and pXY(a,b) by PX(a) and PX(a)pY|X(b|a), respectively, and replace the integral over X by a sum). The maximization in (2.5) is interpreted as constraining pX(■) to satisfy (2.4). The maximum entropy theorem [34, p. 234] establishes that the best X is Gaussian with zero mean and variance P, and the capacity is
where
is the signal-to-noise ratio (SNR) [34, p. 241]. Suppose next that X, h, and![]() are complex with
are complex with![]() , and Zr and Zj are independent, real, Gaussian random variables with variance N/2. The capacity is now
, and Zr and Zj are independent, real, Gaussian random variables with variance N/2. The capacity is now
Modulation
Consider the AWGN channel (2.3) with complex symbol alphabets. Let the SNR in decibels be
so that we can write the capacity (2.8) as
We plot (2.10) in Figure 2.3 as the curve labeled "Gaussian."
Fig. 2.3 Capacity of M-PSK signal sets.
The formula (2.10) is based on using X = XR + jXj, where XR and X/ are independent, real, zero-mean, Gaussian random variables with variance P/2. However, for practical reasons such as amplifier constraints, receiver synchronization, and detector complexity, one usually restricts attention to X with a limited number of values. For example, for wireless communication one might restrict attention to M-ary phase-shift keying (M-PSK) where X is uniform over the alphabet
where Es = P is the (average) per-symbol-energy. The set X is called the signal set or the modulation set (cf. [148, Ch. 4]).
The capacity of the complex AWGN channel with M-PSK is (see (2.5))
where
and
where ZR and Zj are independent, Gaussian, and have variance N/2, and K{x} and 9{x} are the respective real and imaginary parts of x. Suppose we use M = 2,3,4,8, whose signal sets are called binary PSK (BPSK), 3-PSK, quaternary PSK (QPSK) and 8-PSK, respectively. The capacities are plotted in Figure 2.3 as a function of YdB. Observe how the M-PSK capacities saturate at log2(M) bits/use at large 7. Clearly, at high SNRs one must use large signal sets, while at low SNRs it seems that BPSK suffices (however, see the next sections on spectral efficiency).
Finally, we remark that the capacity calculations in this topic assume that the receiver can accurately estimate the channel SNR. If this is not the case, then many interesting issues arise [184]. For instance, an important practical issue is the choice of signal set for the best capacity scaling behavior at low and high SNRs [115, 117].
Spectral Efficiency
We next include the effect of bandwidth. Loosely speaking, the spectral efficiency of a modulation set is the number of bits per second per Hertz that the set can support. To define spectral efficiency more precisely, we follow an approach similar to [165, Sec. VIII] and [188, Sec. 7.2] and make the following idealizations:
(i) The channel passes frequencies f in the range
where the center frequency f0 is much larger than W.2 The equivalent baseband representations of the channel input and
2 Note that W is here the bandwidth rather than a message.
Output signals are therefore complex and band-limited to If | < W/2. We say that the channel bandwidth is W. (ii) The channel is used for a period of T seconds. We describe the channel input and output signals by n = TW complex samples spaced Ts = 1/W seconds apart, i.e., we can reconstruct the baseband input signal X(t) as
where Xi is a complex number whose squared amplitude and phase are the respective energy and phase of the ith input sample. The average energy per sample is
We consider primarily Gaussian signaling for which Xj is a complex Gaussian random variable, or PSK for which |Xj|2 = Es for all i.
(iii) The channel adds complex Gaussian noise with power N to each input sample, i.e., the ith channel output sample is Y = Xi + Zi where Zi = ZR,i + j Z/,i and ZRj and Z/,i are independent, Gaussian random variables each having variance (NTs)/2. Usually N increases proportionally with W, and we write N = WN0 where No/2 is the noise power per Hertz.
The modulation rate is Rmod = log2(M) bits, where M is the number of values that X takes on. For instance, QPSK has Rmod = 2 bits. Suppose the encoder maps blocks of kc bits to blocks of nc bits at the rate Rc = kc/nc. The overall coded modulation rate is therefore R = RcRmod bits. The energy consumed per information bit is Eb = Es/R and we define the information bit SNR ratio as Eb/N0. Let Pb be the decoder bit-error probability.
It is now natural to define the spectral efficiency of the modulation at the bit-error probability Pb as
where R* is the maximum code rate for which one can achieve a bit-error probability of Pb when the information bit SNR ratio is Eb/N0. For wireless transmission Pb can be 10-6, while for optical transmission Pb can be required to be 10-15 or less. However, one usually considers only the case Pb ^ 0 because the spectral efficiency hardly changes as long as Pb < 10-3. We denote the resulting spectral efficiency by n(Eb/Nc).
Note that (2.18) defines spectral efficiency without taking into account the spectral guard bands that are necessary in practice. The reason for doing this is that the amount of guard band needed, in proportion to the bandwidth, will depend primarily on the pulse shape, and less on the number of points in the signal set. We will not consider pulse shaping.
Computing Spectral Efficiency
Recall that we use the channel n = TW times over T seconds, and that the channel is memoryless. The capacity normalized by the time and bandwidth is therefore (see (2.1))
Let Ts = T/n be the symbol time. We are using Ts = 1/W so the denominator of (2.19) is simply one. We further define Es = PTs and Ns = N Ts to be the transmit-symbol and noise-symbol energies, respectively. The mutual information in (2.19) is in general some function of P/N = Es/Ns, i.e., we have
where f is some non-decreasing function, and where we have used Es = REb and Ns = N0(WTs). Note further that R < C, so that C < f (C Eb/N0) and, given Eb/N0, the "best" C is the largest C* satisfying
Equation (2.21) gives the ultimate Eb/N0 in terms of C*, or the ultimate C* in terms of Eb/N0. We thus have
For example, suppose we wish to compute n(Eb/N0) when arbitrary complex X are permitted. Since R mod is in principle infinite here, one now maximizes the overall rate R without separating it into Rmod and Rc. We thus have
We set Es = REb, Ns = N0, and use (2.23) and R < C to obtain
The n which satisfy (2.24) with equality are given by the curve labeled "Gaussian" in Figure 2.4, where (Eb/N0)dB = 10log10Eb/N0. Observe that as n ^ 0 we have Eb/N0 ^ ln(2) w 0.6931 which is -1.59dB.
Fig. 2.4 Spectral efficiencies for M-PSK.
The other curves in Figure 2.4 are those for M-PSK with M = 2,3,4,8. Note the striking differences between Figures 2.4 and 2.3 at low SNRs. Note also that at (Eb/N0)dB w -1.59 dB we have that 3-PSK, QPSK, and 8-PSK all outperform BPSK by a factor of two in rate, but they perform just as well as Gaussian signaling. Thus, BPSK is inefficient at low SNRs, but 3-PSK and QPSK are practically optimal (cf. [183]).
Multi-Antenna Communication
The information theory developed above applies as well to multi-antenna communication. We model such problems by making the channel inputs and outputs vectors, i.e., we have
where X, Y, and Z are complex column vectors of length nx, nY, and nY, respectively, and H is a complex nY x nX matrix. The additive noise vector Z has independent, Gaussian, entries with independent real and imaginary parts with variance N/2 each. The block power constraint is now
where ||X||2 = XfX and X is the complex-conjugate transpose of X.
One can show that the best X are zero-mean and Gaussian by the maximum entropy theorem [34, p. 234]; we write the covariance matrix of X as Qx = E[IIf]. The capacity is (see (2.1))
where (2.28) follows by [34, Thm. 9.4.1], |A| is the determinant of A, and where the maximizations in (2.27) and (2.28) are interpreted as constraining px(■) to satisfy (2.26). Consider the matrix H and recall that we can use the singular value decomposition to write H = VXUt where U and V are unitary and X is a nY x nx matrix that is zero except for the (non-negative) singular values on the diagonal [75, p. 414]. We thus have
where we have used |V| = 1 and VtV = I to remove the V [75, p. 414], and where we have included the U in the optimization of Qx .
The resulting optimization problem is the same as for parallel Gaussian channels [34, p. 250]. The optimal Qx for this problem is known to be diagonal with entries Pi = E[|Xi|2], i = 1,2,…,nX, chosen according to a "waterfilling" solution. More precisely, if we let ai be the ith diagonal entry of E, we choose Pi to satisfy
where the "water level" Q is chosen so that