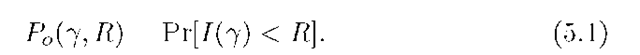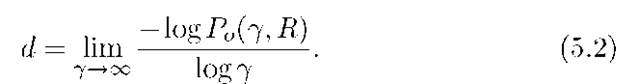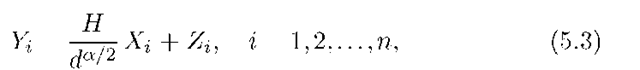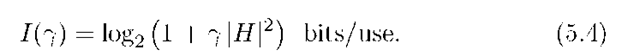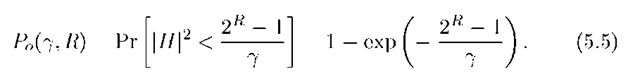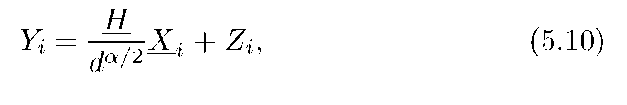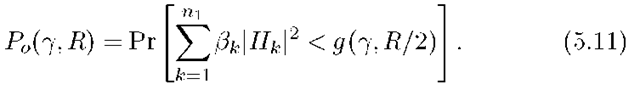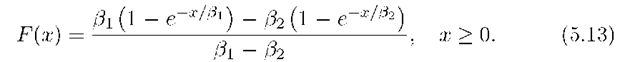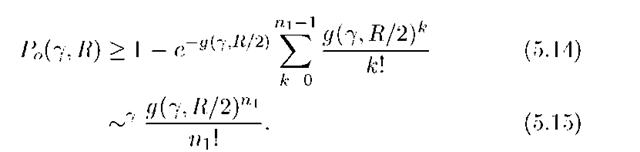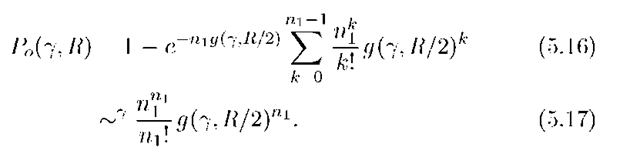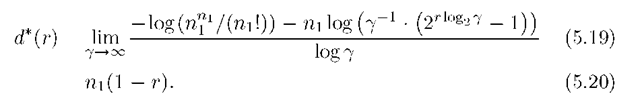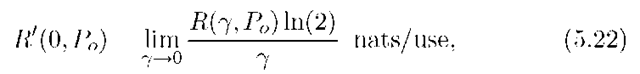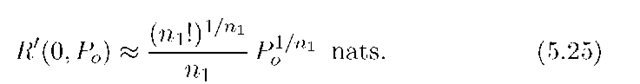Consider a point-to-point channel as in Figure 2.2 and suppose the coded modulation rate is R (see Section 2.2.3). Let 7 be the average SNR at the receiver and let I(7) be the mutual information between the channel inputs and outputs. Observe that I(7) is a random variable that depends on the fading coefficients. We will usually assume that the codeword length n is sufficiently long and the codes sufficiently good so that a decoding error is negligible if I(7) > R. The event I(7) < R is called an outage and we write
We wish to characterize the achievable triples (7, R, Po). For example, for a fixed R and Po we would like to determine the smallest possible 7. However, such an analysis is often difficult so we instead study the limiting behavior of (R, Po) when 7 is large or small. As we shall see, one obtains important insight from these extreme cases.
High SNR Metrics
We consider the following performance metrics for large 7: diversity gain, multiplexing gain, and the diversity-multiplexing tradeoff.
Diversity Gain
For a given rate R, we define the diversity gain to be
The diversity gain thus determines the high-SNR slope of the outage probability as a function of the average SNR when plotted on a log-log scale. For example, consider the slow Rayleigh fading channel with
and the power constraint (2.4), i.e., the Zj and H are the usual complex, Gaussian random variables. Note that H is held fixed for all i and that the expected receive SNR is 7 = (P/N)/da. The mutual information I(7) with Gaussian inputs is
;From (5.4), we thus have
To describe the outage behavior as a function of 7, we use the reciprocal of the normalized SNR (see [52, Sec. II.E])
The outage probability (5.5) is thus
where the notation
means that
Observe from (5.6) and (5.7) that, up to a constant, the outage probability decreases as 1/7 so the diversity gain (5.2) is d = 1.
We remark that for fixed coded modulations such as uncoded BPSK (see Section 2.2.2) we substitute the outage probability Po(Y, R) in (5.2) with the error probability Pe(Y). The BPSK error probability in Rayleigh fading behaves as
and thus BPSK has d = 1 and R = 1.
Finally, we remark that the diversity can alternatively be defined for a family of codes {C(7)} with rates R(y) indexed by 7. In other words, the rate R in (5.2) changes with 7. This extension is useful when studying multiplexing gains.
Diversity Gain for MISO Channels
One can generalize the above analysis for Rayleigh-fading MIMO channels with n1 transmit and n2 receive antennas and show that the diversity gain is d = n1n2 [201]. For example, suppose there are n1 transmit antennas and one receive antenna, i.e., we have a multi-input, single-output or MISO channel. The model is (see Section 4.4)
where
vector with the usual independent Gaussian entries,and the X are n1 x 1 vectors satisfying the power constraint (4.54). Following steps outlined in Section 4.4, one can show that the best X are independent, zero-mean, Gaussian, and with independent entries of variance
The resulting outage probability is
The choice of
, that minimizes Po(Y, R) turns out to depend on 7 and R [174, Section 5.1] and has not yet been characterized for
For n1 = 2, note that
are independent random variables with distribution functions
The distribution function of their sum is
Using (5.13), one can show that the optimal ^ for n1 = 2 are: = = 1/2 if R < log(1 + ^oP) where w 1.2564, and & = 1 otherwise [94].
In general, however, we are mainly interested in large 7 for which one can show that = 1/n1 for all k is best. To see this, note that (5.11) is lower bounded by setting = 1 for all k, i.e., we have (see [148, Ch. 1])
Similarly, if we set ^ = 1/n1 for all k then we can achieve
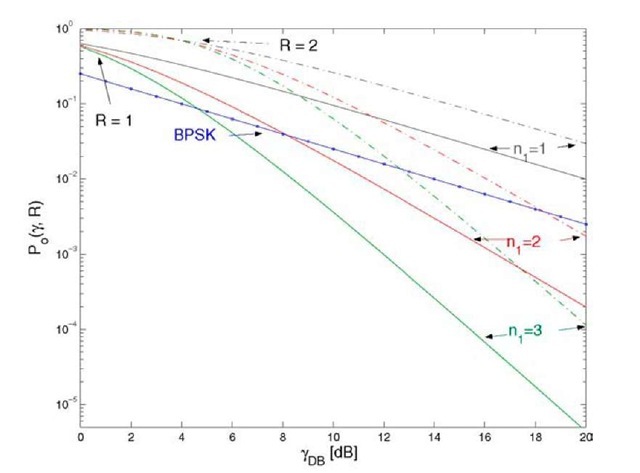
Fig. 5.1 Outage probabilities for MISO channels.
Thus, up to a constant, the outage probability decreases as y-""1 so that the diversity gain (5.2) is d = n1. Figure 5.1 plots P0(y,R) in (5.16) as a function of YdB = 10log10 Y for n1 = 1,2,3 and R = 1,2. Also shown is the BPSK error probability (5.9). Observe that BPSK outperforms the random coding strategies with n1 = 1. However, one should keep in mind that an outage for BPSK means that one bit is in error, while an outage for random codes means that an entire block of bits is in error.
Multiplexing Gain
Suppose we wish to study the limiting behavior of I(y) without considering the outage probability. To do this, we consider a family of codes {c(y)} with rates R(y) indexed by y, as described above. The rates R(y) usually increase with y. The multiplexing gain (or the number of degrees-of-freedom) is defined as
For example, for a Rayleigh-fading MIMO channel with CSIR the maximum multiplexing gain is r = min(n1,n2), which represents the rank of a randomly chosen gain matrix H. We will use R = r log2 7.
Diversity-Multiplexing Tradeoff
To study the diversity and multiplexing gains together, we again consider a family of codes {C(y)} with rates R(y), and we compute the family’s diversity and multiplexing gains using (5.2) and (5.18). It is interesting to characterize the boundary of the set of achievable rate pairs (d,r) over all cooperative protocols. For example, let d*(r) be the supremum of the set of possible d for a fixed r. Similarly, let r*(d) be the supremum of the set of possible r for a fixed d. In analogy to rate-distortion theory, we call d*(-) the diversity-multiplexing function and r*(-) the multiplexing-diversity function.
For example, consider a MISO Rayleigh fading channel with CSIR for which we know that Gaussian inputs with independent entries are optimal. We use (5.17) and R = r log27 to compute
The diversity-multiplexing function is therefore linear. This result generalizes to MIMO channels with n1 transmit and n2 receive antennas as follows. For block lengths n with
we find that
is a piecewise-linear function connecting the points
min(n1,n2), where
(see [201]).
Low SNR Metrics
At low SNR, the system is limited by energy rather than multiplexing gain, and a meaningful metric is the rate R normalized by the SNR [182, 183, 12]. For example, consider the channel (5.3) for which (5.5) gives
where ln(x) is the natural logarithm of x. We define the low-SNR and SNR-normalized rate to be
where we have changed units to nats (1 bit = ln(2) nats). We compute
which gives
nats when Po is small.
Consider next the MISO Rayleigh fading channel (5.10) with n1 transmit antennas and
for all k. We define R’ = Rln(2)/Y nats and use (5.16) to compute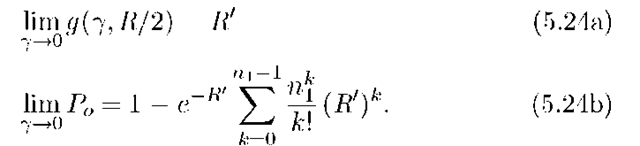
Equation (5.24b) can be solved for R’ as in (5.23), but we will be mainly interested in small Po and hence small R’. Furthermore, small R’ is effectively the same as small g(y,R/2) or large y in (5.14). Ignoring low order terms, for small R’ we have (see [12])
For example, for n1 = 2 and small Po we have
This is much larger than R’(0,Po) w Po for n1 = 1 and small Po.
We remark that we can re-use our high-SNR analysis for low-SNR if we can make the "instantaneous" received SNR large by some means. This is, in fact, possible by using "bursty" transmission where a node signals for a short period of time, or in a small frequency band, with very high power. Of course, such bursty transmission is not possible if one has per-symbol power constraints such as (4.55) or a constraint on the power per Hertz.
