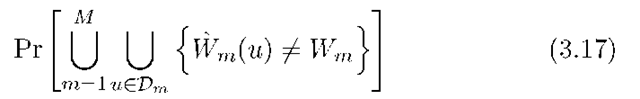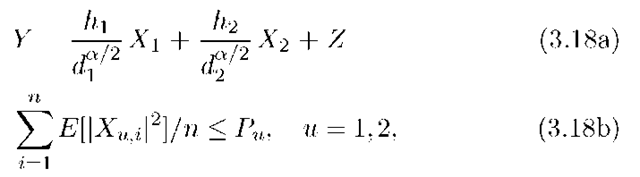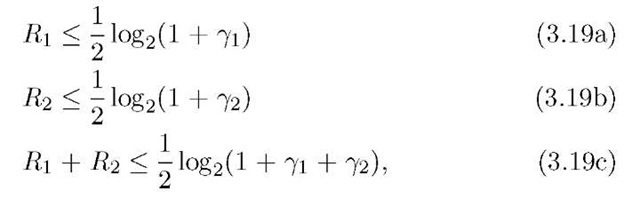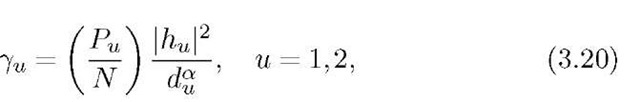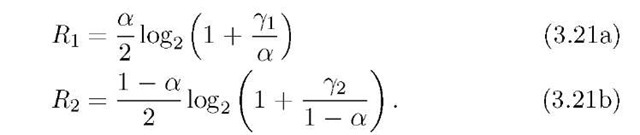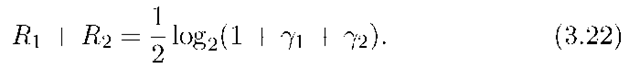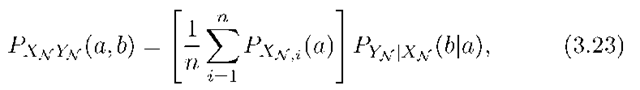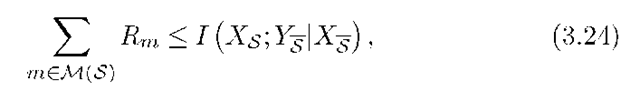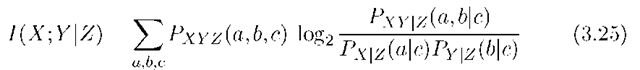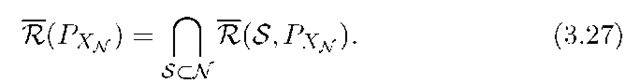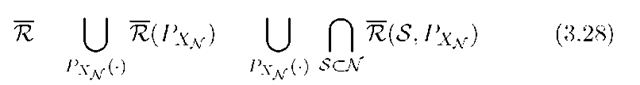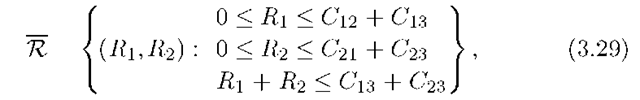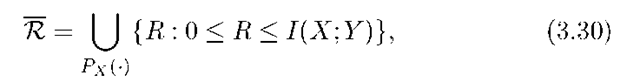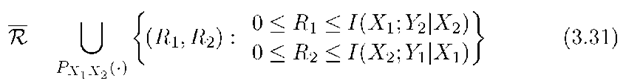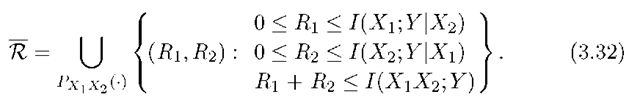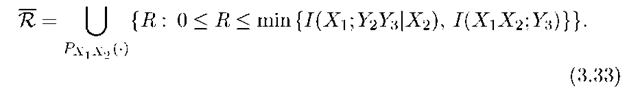In the context of multi-node networks, we would like to define capacity in a similar manner as in Section 2.2.1 for a DMC and AWGN channel. Suppose there are M sources and source m puts out message Wm with bits, m = 1,2,…, M. The messages are assumed to be independent. For convenience, we introduce a common network clock that governs the transmissions of channel inputs Xu,i and outputs Yu,i. Basically, the clock ticks n times and node u can transmit Xu,i after clock tick i — 1 and before clock tick i. Node u receives Yu,i at clock tick i. Hence, Xu,i can be any function of its own messages and its past channel outputs Yui-1 = Yu,1,Yu,2,…,Yu,i-1 [34, p. 444], [27, 102, 167, 180].
The main advantage of introducing a network clock is that it helps to clarify exposition, notation, and concepts such as encoding, decoding, causality, cooperation, relaying, and so forth. An obvious criticism is that a network clock seems artificial and restrictive because all nodes must operate synchronously. However, we remark that node asynchro-nism can often be dealt with by introducing appropriate device constraints on channel knowledge.
A network clock makes it easy to define the capacity of a network. Suppose the network clock ticks n times so that the rate of source message Wm is Rm = Bm/n bits per clock tick. Let Dm be the set of nodes that decode Wm. The capacity region is the closure of the set of rate-tuples (R1 ,R2,…,RM) for which, for sufficiently large n, there exist encoders and decoders so that the error probability can be made as close to 0 as desired (but not necessarily exactly 0).
An interesting fact is that the capacity region is not yet known for any of the memoryless networks in Figures 3.7-3.9 except for the DMC and the MAC. This perhaps surprising situation suggests that finding the information-theoretic capacity regions for networks is a difficult problem indeed. Fortunately, for certain networks with AWGN one can say more. For example, the capacity regions of the 2WC and BC with AWGN are known.1 The capacity regions of the RC, MAC-GF, MAC-DR, and BC-DR have recently been resolved for some cases.
As an example, consider the AWGN MAC with (see Figure 3.7)
where Xu, hu, and Z are real, Z has variance N, and where the expectation is over the codewords. Consider the case Ro = 0. The capacity
The capacity region of the AWGN BC with vector symbols is not yet resolved if Ro > 0, Rl > 0, and R2 > 0.
Region is the set of non-negative rate pairs (R1,R2) in the pentagon defined by the bounds (see [34, p. 405])
where
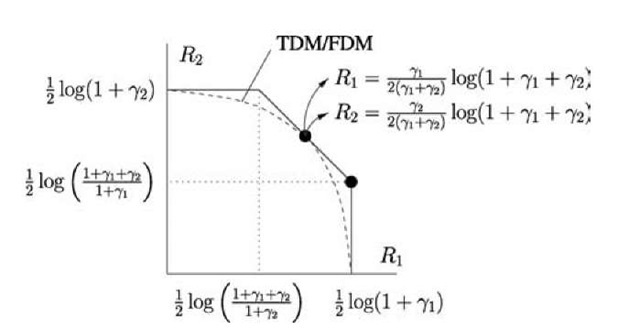
and where the rate units are bits/clock tick. This region is shown in Figure 3.10.
We remark that a simple communication strategy for the MAC with block power constraints (3.18b) is to use time-division multiplexing (TDM) or frequency-division multiplexing (FDM). For example, suppose nodes 1 and 2 use the fractions a and 1 — a of the available bandwidth, respectively. The noise powers for nodes 1 and 2 thus reduce to aN and (1 — a)N, respectively (see Section 2.2.3), and the rates are
Fig. 3.10 AWGN MAC channel capacity region.
Similarly, if nodes 1 and 2 use the fractions a and 1 — a of the available time, then they can boost their powers while transmitting by the factors
and
, respectively. The resulting rate pairs (3.21a) and (3.21b) are plotted in Figure 3.10. In particular, by choosing
one achieves a boundary point with
TDM and FDM are thus effective techniques for the MAC with AWGN. 3.7.1 Cut-Set Bound on Capacity
The capacity of networks is useful to know because it provides a benchmark for what is possible and guides the design of protocols and codes. However, as we have seen, the capacity is often difficult to determine. As a compromise, one is left with trying to find capacity bounds. Inner bounds on the capacity region are based on creatively designing protocols and codes to show that certain rate-tuples are achievable. Outer bounds on the capacity region are, however, often more difficult and tricky to develop as they must hold for all possible protocols and codes. A very useful outer bound for large networks is known as a cut-set bound [34, p. 445], [9, 43, 167].
Suppose that U and V are disjoint subsets of the set N of network device nodes, i.e., N does not include message nodes and message-estimate nodes. Let (U, V) denote the set of edges that lead from U to V. Consider a set ScN and let S be the complement of S in N .A cut separating the message Wm from one of its estimates Wm(u) is a pair (S, S) where the Wm message node is connected to a node in S but not in S, and where the Wm(u) message-estimate node is connected to a node in S.
The above definition of a cut is the same as the usual notion of a cut in wireline networks. Furthermore, there is a cut-set bound that we develop below that applies to all the networks considered in this topic. For directed wireline networks, this bound reduces to the usual cut-set bound, but we caution that for undirected wireline networks the following bound can be better than standard bounds [108].
Let
and similarly for Ys . Consider any choice of encoders and decoders, and suppose we compute the per-clock-tick average joint distribution
where PXNi is the marginal distribution of the channel inputs at time i. Let M(S) be the set of messages separated from one of their sinks by the cut (S, S). Then any rate-tuple in the capacity region must satisfy
where for discrete alphabets
is the mutual information between X and Y conditioned on Z. The expression (3.25) generalizes to continuous alphabets in natural ways. Furthermore, if node u has the power constraint (3.18b), then we require
Next, for a given input distribution PXn(■) satisfying (3.26), let R(S,PXn) be the set of non-negative rate-tuples satisfying (3.24). We further define
The cut-set bound is the union of (3.27) over all input distributions, i.e., the cut-set region is
and R is an outer bound on the capacity region.
A few remarks are in order. First, we emphasize that if Px is fixed then (3.27) is itself an upper bound on the achievable rates. Second, one can show that
in (3.24) is concave in PXn. Finding boundary points of (3.28) in terms of PXn is therefore a concave optimization problem because the intersection of concave functions is concave. Finally, we remark that R is the best known capacity outer bound even for many small networks.
For example, consider the wireline network in Figure 3.4 but without the port constraints (3.2). Suppose the capacity of edge (u,v) is Cuv and nodes 1 and 2 have messages W1 and W2, respectively, destined for node 3. The cut-set bound is
where the optimal input distribution has the Xuv being independent and uniform. It turns out that the cut-set bound is the capacity region in this case, and it is also the usual networking cut-set bound. Consider next some networks with noise. For the DMC we have
which is consistent with (2.1). For the 2WC, we have
and it remains to optimize over the joint distribution PXlX2. For the MAC with output Y, we obtain
We again must optimize over PXlX2. For the RC, we have
In fact, the cut-set bounds (3.31)-(3.33) are loose in general because optimizing over all PXlX2 (■) is too optimistic (although anticipated, the bound (3.33) was only recently shown to be loose for a class of RCs [6]). Nevertheless, the cut-set bound often provides a useful benchmark, and it sometimes even gives the capacity region. As a final remark, one can improve cut-set bounds by using an approach that progressively removes edges from the network graph [107, 109].
