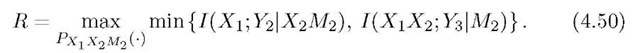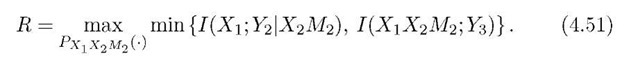The information theory developed in the previous sections applies to both full-duplex and half-duplex devices [106]. In this section, we consider the theory in more detail for half-duplex devices. For example, we demonstrate that half-duplex nodes can transmit data by modulating their "listen" to "talk" modes [103]. However, despite their fundamental nature, one might not want to harness such mode modulation gains for reasons outlined below.
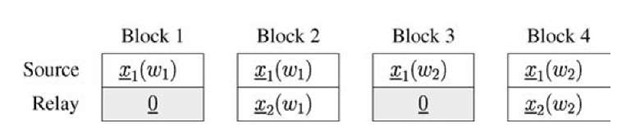
Consider a half-duplex RC with no fading. A DF strategy is depicted in Figure 4.22 where the relay listens for some fraction of the time and talks for the other fraction of the time.6 Furthermore, all nodes know ahead of time when the relay listens and talks. We include the relay’s operating modes explicitly in the model as follows [103]. Let M2 be a mode random variable that takes on the values M2 = L and M2 = T if the relay listens and talks, respectively. One can check that the DF 6 Observe that the relay decodes all message blocks wj.
Fig. 4.22 A DF strategy for a half-duplex relay channel.
Strategy in Figure 4.22 achieves the rate
However, suppose we re-define the channel as
where the relay’s channel input is
. We use X2 in place of X2 in (4.32) and find that the DF rate is
Expanding the second term on the right in (4.51), we have
and one can check that
in general. Thus, a strategy with pre-assigned slots such as in Figure 4.22 is generally suboptimal.
The reason for the rate gain
in (4.52) is that the relay sends information to the destination through its choice of operating mode. In fact, this is how we achieve the wireline network capacity in Section 4.1.3. Mode modulation further improves all the strategies considered in Section 4.2, i.e., AF, classic multi-hop, CF, and DF or MDF with network coding. At the same time, there are some challenges.
(1) I(M2; Y3) is limited to 1 bit/clock tick because M2 is binary. Thus, mode modulation cannot help much for channels with high capacity, e.g., wireline packet networks with large packets (see Section 4.1.3) or AWGN channels with high SNR.
(2) The rate gain requires M2 to change rapidly. However, wireline or wireless nodes cannot always switch from "listen" to "talk" modes rapidly.
(3) A remedy for the switching problem is to constrain the M2 sequence to change slowly, e.g., via run-length limited codes. However, this limits the rate gain even further.
The above reasons, as well as other considerations, usually lead one to choose strategies as in Figure 4.22. We will do the same below (see also [76, 98]). First, however, we show that mode modulation can give rate gains [103].
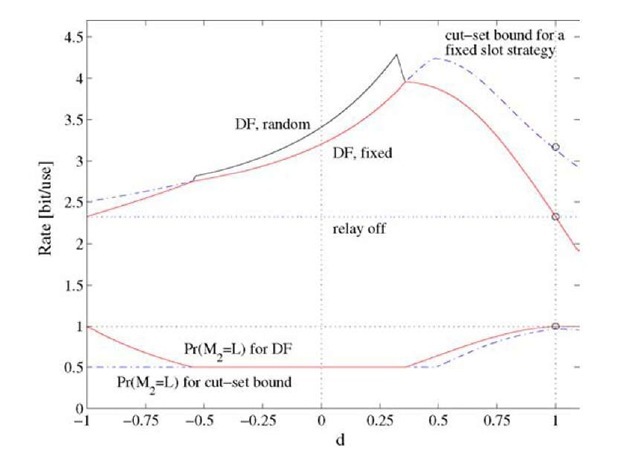
Consider the general relay geometry of Figure 4.8(a) and suppose there is no fading with Huv = 1 for all (u, v) and a = 4. Suppose further that we have per-symbol power-constraints P1 = P2 = 4, and that the relay must listen at least half the time to guarantee cooperation, i.e., PM2 (L) > 0.5. The DF rates (4.51), where the relay turns on and off randomly, are shown in Figure 4.23 as the curve labeled "DF, random." The DF rates (4.50), where the relay turns on and off at fixed time-intervals, are shown as the curve labeled "DF, fixed." The upper dash-dotted curve is the cut-set bound when using strategies as in Figure 4.23, and it is computed as (4.50) but with Y2 replaced by [Y2 Y3]. Note that mode modulation outperforms any type of strategy with pre-assigned slots. The lower curves in Figure 4.23 show the optimizing PM2 (L) for both (4.50) and the cut-set bound.
Fig. 4.23 Rates for half-duplex strategies with Pi = P2 = 4, Huv = 1 for all (u,v), and a = 4.
