Abstract. We introduce the concept of vision-realistic rendering – the computer generation of synthetic images that incorporate the characteristics of a particular individual’s entire optical system. Specifically, this paper develops a method for simulating the scanned foveal image from wavefront data of actual human subjects, and demonstrates those methods on sample images.
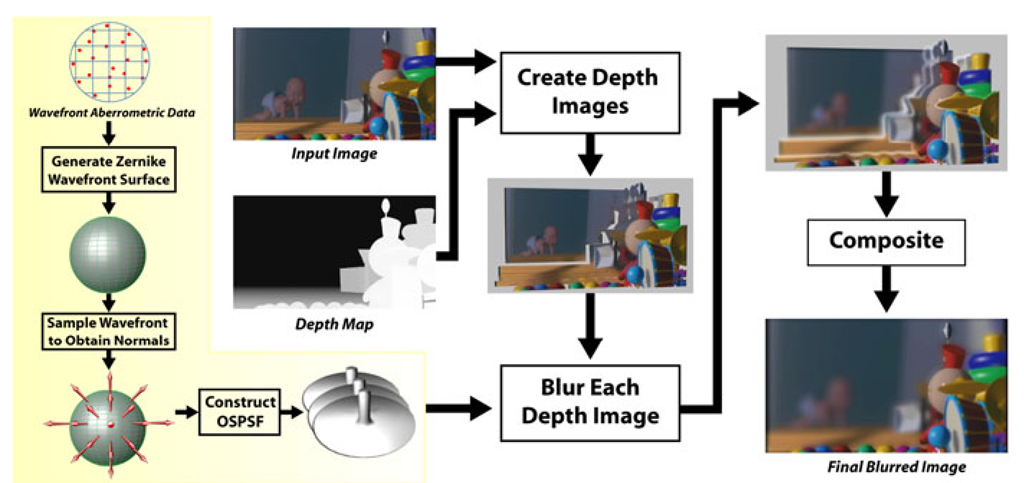
First, a subject’s optical system is measured by a Shack-Hartmann wavefront aberrometry device. This device outputs a measured wavefront which is sampled to calculate an object space point spread function (OSPSF). The OSPSF is then used to blur input images. This blurring is accomplished by creating a set of depth images, convolving them with the OSPSF, and finally compositing to form a vision-realistic rendered image.
Although processing in image space allows an increase in speed, the images may have artifacts introduced due to occlusion or discretization. Two approaches for object identification to properly blur the scene are discussed.
Applications of vision-realistic rendering in computer graphics as well as in optometry and ophthalmology are discussed.
keywords vision-realistic rendering, optics, ray tracing, image synthesis, human visual system, blur, optometry, ophthalmology, LASIK, pupil, Point Spread Function (PSF),
Introduction
After the development of the fundamentals of raster graphics in the 1970’s, advances in computer graphics in the 1980’s were dominated by the quest for photorealistic rendering, and attention turned to non-photorealistic rendering in the 1990’s. For the first decade of the the 21st century, we propose to extend this to vision-realistic rendering (VRR). VRR is the simulation of the actual human vision of a particular subject – not merely a model of vision, but the generation of images that incorporate characteristics of a particular individual’s optical system.
Such an ambitious undertaking will require the integration of many fields of study, beyond the traditional ones for computer graphics, such as physiological optics, human visual perception, psychophysics of vision, visual neurophysiology, human color vision, binocular vision, visual sensory mechanisms, etc.
Fig. 1. Vision-realistic rendered image simulating vision based on actual wavefront data from a patient with keratoconus
To embark upon this endeavor, we begin with the problem of simulating the retinal image formed by the optics of the eye. Since the goal is to simulate vision of an actual human subject, not just to use a model, we need data about the optics of the subject’s eye.
Ideally, we would like to have data about the aberrations of these optics for each photoreceptor across the retina. That is, given a gaze direction, we would like to trace a ray from each photoreceptor, through the optical structures of the eye such as the internal crystalline lens and cornea, out into the environment, and measure the aberrations for that ray, including whatever would arise given the current accommodative state of the crystalline lens of the eye.
Unfortunately, such capability does not exist at the present time. That deficiency notwithstanding, it is exciting to note that we can achieve an approximation to such measurements using recently-developed technology motivated by the goal of improving laser corneal photoreactive vision correction surgeries such as LASIK (laser in-situ keratomileusis). This technology is wavefront aberrometry, that is, instruments that measure the wavefront emerging from the eye and quantify the amount of each different kind of optical aberration present. The limitation is that the instrument does so at only one point in the retina.
However, that limitation is not nearly as much of a problem as it may seem at “first glance”. The reason is that the arrangement of photoreceptors on the retina is not at all the uniform structure that we are used to in raster graphics where pixels are arranged in neat, rectangular arrays. Rather, the cones are densely packed in a small area in the middle of the cornea, called the fovea, and are much more sparsely arranged towards the periphery. The fovea is approximately 600 microns wide and subtends an angle of view of about two degrees. When one looks at an object, the eye is oriented such that light comes to a focus in this foveal region of the retina. Consequently, if we use wavefront aberrometry to measure the aberrations present for vision at a point in this foveal region, we will have a reasonable first approximation to the image perceived by the subject.
The reason that this approximation works so well is that when looking at a scene, a viewer naturally and involuntarily quickly scans around the scene at different objects. At any instant, the viewer is focused at only one object, using high resolution foveal vision. However, by scanning around the scene, the viewer gains the misleading impression that the entire scene has been viewed in this high resolution vision. But at any instant, in fact, it is only the object in the center of visual field that is seen in high resolution. The periphery of the scene is really being viewed in much lower resolution vision, even though that is not evident.
Ergo, our approach is to obtain the wavefront aberrometry from a point in the fovea, and then to simulate the vision as if the aberrations were constant across the visual field.
This paper describes a pipeline to simulate the scanned foveal image from wavefront data of actual human subjects, and shows some example images. These are the first images in computer graphics that are generated on the basis of the specific optical characteristics of actual individuals.
Optometry and Ophthalmology Motivation
In practice poor visual performance is often attributed to simple blur; however, our technique enables the generation of vision-realistic rendered images and animations that demonstrate specific defects in how a person sees. Such images of simulated vision could be shown to an individual’s eye care clinician to convey the specific visual anomalies of the patient. Doctors and patients could be educated about particular vision disorders by viewing images that are generated using the optics of various ophthalmic conditions such as keratoconus (Figure 1) and monocular diplopia.
One of the most compelling applications is in the context of vision correction using laser corneal refractive eye surgeries such as PRK (photorefractive keratectomy) and LASIK (laser in-situ keratomileusis). Currently, in the United States alone, a million people per year choose to undergo this elective surgery. By measuring subjects pre-operatively and post-operatively, our technique could be used to convey to doctors what the vision of a patient is like before and after surgery (Figures 20 and 21). In addition, accurate and revealing medical visualizations of predicted visual acuity and of simulated vision could be provided by using modeled or adjusted wavefront measurements. Potential candidates for such surgery could view these images to enable them to make more educated decisions regarding the procedure. Still another application would be to show such candidates some of the possible visual anomalies that could arise from the surgery, such as glare at night. With the increasing popularity of these surgeries, perhaps the current procedure which has patients sign a consent form that can be difficult for a layperson to understand fully could be supplemented by the viewing of a computer-generated animation of simulated vision showing the possible visual problems that could be engendered by the surgery.
Previous and Related Work
For a discussion of camera models and optical systems used in computer graphics, the reader is referred to a pair of papers by Barsky et al. where the techniques have been separated into object space [1] and image space [2] techniques.
The first synthetic images with depth of field were computed by Potmesil and Chakravarty [3] who convolved images with depth-based blur filters. However, they ignored issues relating to occlusion, which Shinya [4] subsequently addressed using a ray distribution buffer. Rokita [5] achieved depth of field at rates suitable for virtual reality applications by repeated convolution with 3 x 3 filters and also provided a survey of depth of field techniques [6]. Although we are also convolving images with blur filters that vary with depth, our filters encode the effects of the entire optical system, not just depth of field. Furthermore, since our input consists of two-dimensional images, we do not have the luxury of a ray distribution buffer. Consequently, we handle the occlusion problem by the techniques described in Section 6 and in more detail by Barsky et al. [7] [8].
Stochastic sampling techniques were used to generate images with depth of field as well as motion blur by Cook et al. [9], Dippe and Wold [10], and Lee et al. [11]. More recently, Kolb et al. [12] described a more complete camera lens model that addresses both the geometry and radiometry of image formation. We also use stochastic sampling techniques for the construction of our OSPSF.
Loos et al. [13] used wavefront tracing to solve an optimization problem in the construction of progressive lenses. They also generated images of three dimensional scenes as viewed through a simple model eye both with and without progressive lenses. However, while we render our images with one point of focus, they chose to change the accommodation of the virtual eye for each pixel to “visualize the effect of the lens over the full field of view” [13]. Furthermore, our work does not rely on a model of the human optical system, but instead uses actual patient data in the rendering process.
Light field rendering [14] and lumigraph systems [15] were introduced in 1996. These techniques represent light rays as a pair of interactions of two parallel planes. This representation is a reduction of the plenoptic function, introduced by Adelson and Bergen [16]. The algorithms take a series of input images and construct the scene as a 4D light field. New images are generated by projecting the light field to the image plane. Although realistic object space techniques consume a large amount of time, Heidrich et al. [17] used light fields to describe an image-based model for realistic lens systems that could attain interactive rates by performing a series of hardware accelerated perspective projections. Isaksen et al. [18] modeled depth of field effects using dynamically reparameterized light fields. We also use an image-based technique, but do not use light fields in our formulation.
There is a significant and somewhat untapped potential for research that addresses the role of the human visual system in computer graphics. One of the earliest contributions, Upstill’s Ph.D. dissertation [19], considered the problem of viewing synthetic images on a CRT and derived post-processing techniques for improved display. Spencer et al. [20] investigated image-based techniques of adding simple ocular and camera effects such as glare, bloom, and lenticular halo. Bolin and Meyer [21] used a perceptually-based sampling algorithm to monitor images as they are being rendered for artifacts that require a change in rendering technique. [22-26] and others have studied the problem of mapping radiance values to the tiny fixed range supported by display devices. They have described a variety of tone reproduction operators, from entirely ad hoc to perceptually based. For a further comparison of tone mapping techniques, the reader is referred to [27]. Meyer and Greenberg [28] presented a color space defined by the fundamental spectral sensitivity functions of the human visual system. They used this color space to modify a full color image to represent a color-deficient view of the scene. Meyer [29] discusses the first two stages (fundamental spectral sensitivities and opponent processing) of the human color vision system from a signal processing point of view and shows how to improve the synthesis of realistic images by exploiting these portions of the visual pathway. Pellacini et al. [30] developed a psychophysically-based light reflection model through experimental studies of surface gloss perception. Much of this work has focused on human visual perception and perceived phenomena; however, our work focuses exclusively on the human optical system and attempts to create images like those produced on the retina. Perceptual considerations are beyond the scope of this paper.
In human vision research, most simulations of vision [31, 32] have been done by artist renditions and physical means, not by computer graphics. For example, Fine and Rubin [33, 34] simulated a cataract using frosted acetate to reduce image contrast. With the advent of instruments to measure corneal topography and compute accurate corneal reconstruction, several vision science researchers have produced computer-generated images simulating what a patient would see. Principally, they modify 2D test images using retinal light distributions generated with ray tracing techniques. Camp et al. [35, 36] created a ray tracing algorithm and computer model for evaluation of optical performance. Maguire et al. [37, 38] employed these techniques to analyze post-surgical corneas using their optical bench software. Greivenkamp [39] created a sophisticated model which included the Stiles-Crawford effect [40], diffraction, and contrast sensitivity. A shortcoming of all these approaches is that they overlook the contribution of internal optical elements, such as the crystalline lens of the eye.
Garcia, Barsky, and Klein [41-43] developed the CWhatUC system, which blurs 2D images to produce an approximation of how the image would appear to a particular individual. The system uses a reconstructed corneal shape based on corneal topography measurements of the individual. Since the blur filter is computed in 2D image space, depth effects are not modeled.
The latter technique, like all those that rely on ray casting, also suffers from aliasing problems and from a computation time that increases with scene complexity. These problems are exacerbated by the need to integrate over a finite aperture as well as over the image plane, driving computation times higher to avoid substantial image noise. Since our algorithms are based in image space, they obviate these issues. That notwithstanding, the source of our input images would still need to address these issues. However, since our input images are in sharp focus, the renderer could save some computation by assuming a pinhole camera and avoiding integration over the aperture.
Vision-Realistic Rendering was introduced to the computer graphics community by the author in [44] and [45], and is presented in more detail here.
Fig. 2. Overview of the vision-realistic rendering algorithm
Shack-Hartmann Device
The Shack-Hartmann Sensor [46] (Figure 3) is a device that precisely measures the wavefront aberrations, or imperfections, of a subject’s eye [47]. It is believed that this is the most effective instrument for the measurement of human eye aberrations [48]. A low-power 1 mm laser beam is directed at the retina of the eye by means of a halfsilvered mirror, as in Figure 4.
The retinal image of that laser now serves as a point source of light. From its reflection, a wavefront emanates and then moves towards the front of the eye. The wavewfront passes through the eye’s internal optical structures, past the pupil, and eventually out of the eye. The wavefront then goes through a Shack-Hartmann lenslet array to focus the wavefront onto a CCD array, which records it.
The output from the Shack-Hartmann sensor is an image of bright points where each lenslet has focused the wavefront. Image processing algorithms are applied to determine the position of each image blur centroid to sub-pixel resolution and also to compute the deviation from where the centroid would be in for an ideal wavefront. The local slope of the wavefront is determined by the lateral offset of the focal point from the center of the lenslet. Phase information is then derived from the slope [49]. Figures 5 and 6 show the Shack-Hartmann output for eyes with and without aberrations. Figure 7 illustrates the actual output of a Shack-Hartmann sensor for a sample refractive surgery patient.