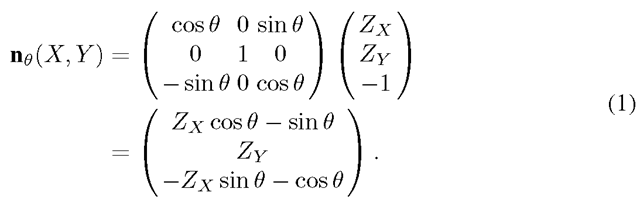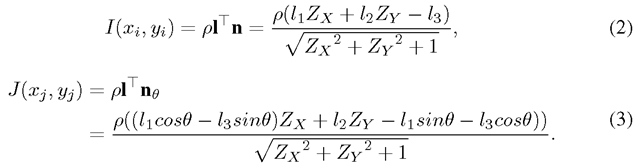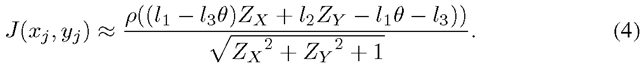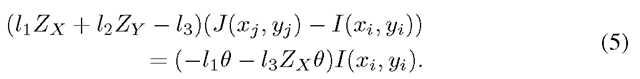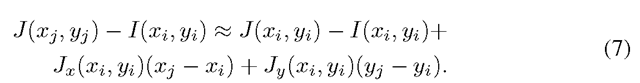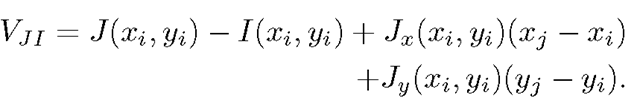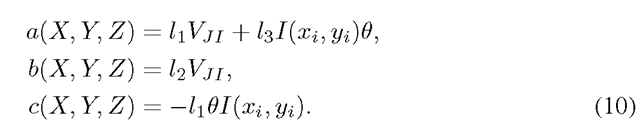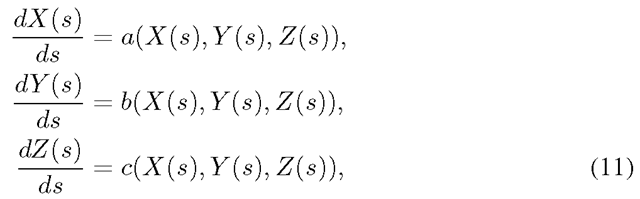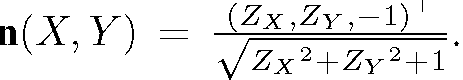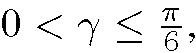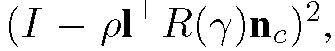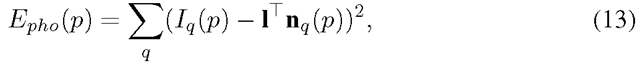Abstract. This paper addresses the problem of shape from shadings under perspective projection and turntable motion.Two-Frame-Theory is a newly proposed method for 3D shape recovery. It estimates shape by solving a first order quasi-linear partial differential equation through the method of characteristics. One major drawback of this method is that it assumes an orthographic camera which limits its application. This paper re-examines the basic idea of the Two-Frame-Theory under the assumption of a perspective camera, and derives a first order quasi-linear partial differential equation for shape recovery under turntable motion. The Dirichlet boundary condition is derived based on Dynamic programming. The proposed method is tested against synthetic and real data. Experimental results show that perspective projection can be used in the framework of Two-Frame-Theory, and competitive results can be achieved.
Keywords: Two-Frame-Theory, Perspective projection, Shape recovery, Turntable motion.
Introduction
Shape recovery is a classical problem in computer vision. Many constructive methods have been proposed in the literature. They can generally be classified into two categories, namely multiple-view methods and single-view methods. Multiple-view methods such as structure from motion [7] mainly rely on finding point correspondences in different views, whereas single-view methods such as photometric stereo use shading information to recover the model.
Multiple-view methods can be further divided into point-based methods and silhouette-based methods. Point-based methods are the oldest technique for 3D reconstruction [5]. Once feature points across different views are matched, the shape of the object can be recovered. The major drawback of such methods is that they depend on finding point correspondences between views. This is the well-known correspondence problem which itself is a very tough task. Moreover, point-based methods do not work for featureless object. On the other hand, silhouette-based methods are a good choice for shape recovery of featureless object. Silhouettes are a prominent feature in an image, and they can be extracted reliably even when no knowledge about the surface is available. Silhouettes can provide rich information for both the shape and motion of an object [8,3]. Nonetheless, only sparse 3D points or a very coarse visual hull can be recovered if the number of images used for reconstruction is comparatively small. Photometric stereo, which is a single-view method, uses images taken from one fixed viewpoint under at least three different illumination conditions. No image correspondences are needed. If the albedo of the object and the lighting directions are known, the surface orientations of the object can be determined and the shape of the object can be recovered via integration [9]. However, most of the photometric stereo methods consider orthographic projection. Few works are related to perspective shape reconstruction [6]. If the albedo of the object is unknown, photometric stereo may not be feasible.
Very few studies in the literature use both shading and motion cues under a general framework. In [2], the 3D reconstruction problem is formulated by combining the lighting and motion cues in a variational framework. No point correspondences is needed in the algorithm. However, the method in [2] is based on optimization and requires piecewise constant albedo to guarantee convergence to a local minimum. In [11], Zhang et al. unified multi-view stereo, photometric stereo and structure from motion in one framework, and achieved good reconstruction results. Their method has a general setting of one fixed light source and one camera, but with the assumption of an orthographic camera model. Similar to [2] , the method in [11] also greatly depends on optimization. A shape recovery method was proposed in [4] by utilizing the shading and motion information in a framework under a general setting of perspective projection and large rotation angle. Nonetheless, it requires that one point correspondence should be known across the images and the object should have an uniform albedo.
A Two-Frame-Theory was proposed in [1] which models the interaction of shape, motion and lighting by a first order quasi-linear partial differential equation. Two images are needed to derive the equation. If the camera and lighting are fully calibrated, the shape can be recovered by solving the first order quasi-linear partial differential equation with an appropriate Dirichlet boundary condition. This method does not require point correspondences across different views and the albedo of the object. However, it also has some limitations. For instance, it assumes an orthographic camera model which is a restrictive model. Furthermore, as stated in the paper, it is hard to use merely two orthographic images of an object to recover the angle of out-of-plane rotations.
This paper addresses the problem of 3D shape recovery under a fixed single light source and turntable motion. A multiple-view method that exploits both motion and shading cues will be developed. The fundamental theory of the Two-Frame-Theory will be re-examined under the more realistic perspective camera model. Turntable motion with small rotation angle is considered in this paper. With this assumption, it is easy to control the rotation angle compared to the setting in [1]. A new quasi-linear partial differential equation under turntable motion is derived, and a new Direchlet boundary condition is obtained using dynamic programming. Competitive results are achieved for both synthetic and real data.
This paper is organized as follows: Section 2 describes the derivation of the first order quasi-linear partial differential equation. Section 3 describes how to obtain the Dirichlet boundary condition. Section 4 shows the experimental results for synthetic and real data. A brief conclusion is given in Section 5.
First Order Quasi-linear PDE
Turntable motion is considered in this paper. Similar to the setting in [1], two images are used to derive the first order quasi-linear partial differential equation (PDE). Suppose that the object rotates around the Y-axis by a small angle. Let X = (X, Y, Z) denotes the 3D coordinates of a point on the surface. The projection of X in the first image is defined as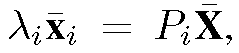
where Pi is the projection matrix, X is the homogenous coordinates of X and xi is the homogenous coordinates of the image point. Similarly, the projection of X after the rotation is defined as
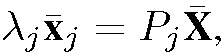where Pj is the projection matrix after the rotation. The first image can be represented by
is the inhomogeneous coordinates of the image point. Similarly the second image can be represented by
. Let the surface of the object be represented by Z(X, Y).
Suppose that the camera is set on the negative Z-axis. The unit normal of the surface is denoted by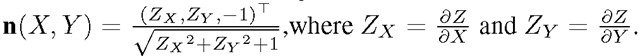
After rotating the object by a small angle θ around the Y-axis, the normal of the surface point becomes
Directional light is considered in this paper and it is expressed as a vector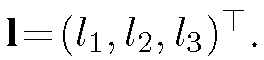
Since the object is considered to have a lambertian surface, the intensities of the surface point in the two images are given by
where ρ is the albedo for the current point. If θ is very small, (3) can be approximated by
The albedo and the normal term (denominator) can be eliminated by subtracting (2) from (4), and dividing the result by (2). This gives
Note that some points may become invisible after rotation and that the correspondences between image points are unknown beforehand. If the object has a smooth surface, the intensity of the 3D point in the second image can be approximated by its intensity in the first image through the first-order 2D Taylor series expansion:
Therefore,
Substituting (7) into (5) gives
where
Note that
are functions of X, Y, and Z, and (8) can be written more succinctly as
where
(9) is a first-order partial differential equation in Z(X,Y). Furthermore, it is a qusi-linear partial differential equation since it is linear in the derivatives of Z, and its coefficients, namely a(X, Y, Z), b(X, Y, Z), and c(X, Y, Z), depend on Z. Therefore, the shape of the object can be recovered by solving this first order quasi-linear partial differential equation using the method of characteristics. The characteristic curves can be obtained by solving the following three ordinary differential equations:
where s is a parameter for the parameterization of the characteristic curves. [1] has given a detailed explanation of how the method of characteristics works. It is also noticed that the quasi-linear partial differential equation should have a unique solution. Otherwise, the recovered surface may not be unique. In the literature of quasi-linear partial differential equation, this is considered as the initial problem for quasi-linear first order equations. A theorem in [10] can guarantee that the solution is unique in the neighborhood of the initial boundary curve. However, the size of the neighborhood of the initial point is not constrained. It mainly depends on the differential equation and the initial curve. It is very important to find an appropriate Dirichlet boundary. In this paper, dynamic programming is used to derive the boundary curve.
Boundary Condition
Under perspective projection, the Dirichlet Boundary condition cannot be obtained in the same way as in [1]. As noted in [1], the intensities of the contour generator points are unaccessible. Visible points (X’, Y’, Z’) nearest to the contour generator are a good choice for boundary condition. If the normal n’ of (X’, Y’, Z’) is known, Zx and Zy
can be derived according to i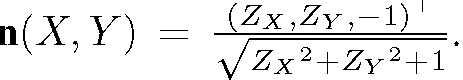
Note that (9) also holds for (X’, Y’, Z’). Therefore, (X’, Y’, Z’) can be obtained by solving (9) with known Zx and Zy values. The problem of obtaining (X’, Y’, Z’) becomes the problem of how to obtain n’.
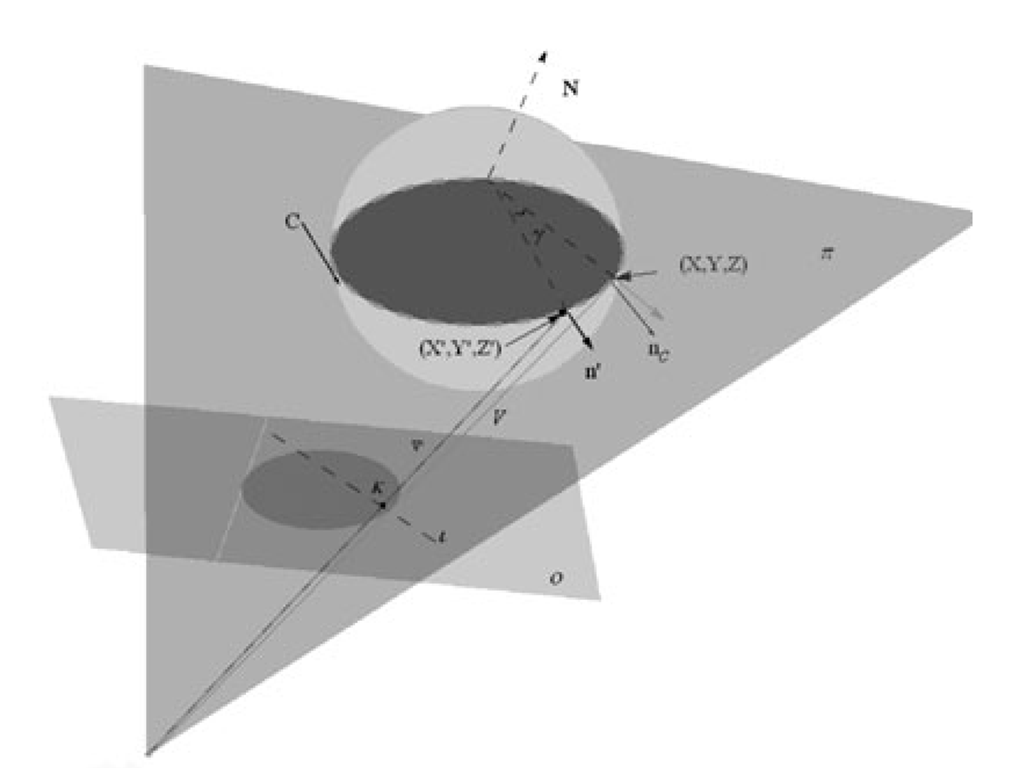
Let (X, Y, Z) be a point on the contour generator (see Figure 1). Since (X, Y, Z) is a contour generator point, its normal nc must be orthogonal to its visual ray V. Consider a curve C given by the intersection of the object surface with the plane π defined by V and nc. In a close neighborhood of (X, Y, Z), the angle between V and the surface normal along C would change from just smaller than 90 degrees to just greater than 90 degrees. Now consider a visible point (X’, Y’, Z’) on C close to (X, Y, Z), its normal n’ should make an angle of just smaller than 90 degrees with V. If (X ‘, Y ‘, Z’) is very close to (X, Y, Z), n’ would also be very close to nc. To simplify the estimation of n’, it is assumed that n’ is coplanar with nc and lying on π. n’ can therefore be obtained by rotating nc around an axis given by the normal N of π by an arbitrary angle γ. According to the lambertian law, n’ can be obtained by knowing the intensities of corresponding points across different views and the albedo. However, no prior knowledge of point correspondences and albedo ρ are available. Similar to the solution in [1], ρ and γ can be obtained alternatively. The image coordinates of the visible point nearest to the contour generator can be obtained by searching along a line I determined by the intersection of the image plane o and π. As for each 7 in the range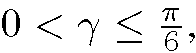
a corresponding albedo is computed and ρ is chosen as the mean of these computed values. γ is then computed by minimizing
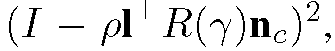where R(y) is the rotation matrix defined by the rotation axis I and rotation angle γ. n’ is finally determined as R(Y)nc and (X’, Y’, Z’) can be obtained by minimizing
Dynamic programming is used to obtain (X’,Y’, Z’). Two more constraints are applied in the framework of dynamic programming. One is called photometric consistency which is defined as
where p is a 3D point on the contour generator, and Iq (p) is a component of the normalized intensity measurement vector which is composed of the measurement of intensities in q neighboring views and nq (p) is the normal of p in the qth neighboring view.
The other constraint is called surface smoothness constraint which is defined as:
where pos(p) denotes the 3D coordinates of point p and pos(p’) denotes the 3D coordinates of its neighbor point p’ along the boundary curve.
Fig. 1. Computing boundary condition. The visible curve nearest to contour generator is a good choice for the boundary condition. The curve can be obtained by searching the points whose normal is coplanar with those of the respective contour generator points.
The final Energy function is defined as
where μ, η, ω are weighting parameters. By minimizing (15) for each visible point nearest to the contour generator, the nearest visible boundary curve can be obtained and used as Dirichlet Boundary condition for solving (9).
