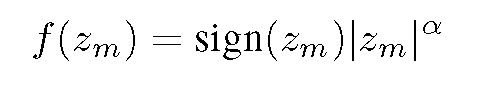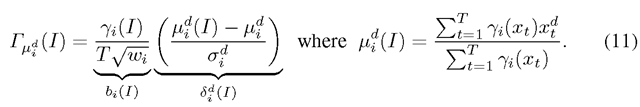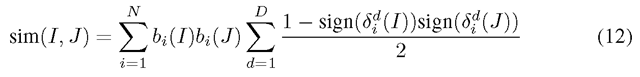Abstract. The Fisher Vector (FV) representation of images can be seen as an extension of the popular bag-of-visual word (BOV). Both of them are based on an intermediate representation, the visual vocabulary built in the low level feature space. If a probability density function (in our case a Gaussian Mixture Model) is used to model the visual vocabulary, we can compute the gradient of the log likelihood with respect to the parameters of the model to represent an image. The Fisher Vector is the concatenation of these partial derivatives and describes in which direction the parameters of the model should be modified to best fit the data. This representation has the advantage to give similar or even better classification performance than BOV obtained with supervised visual vocabularies, being at the same time class independent. This latter property allows its usage both in supervised (categorization, semantic image segmentation) and unsupervised tasks (clustering, retrieval). In this paper we will show how it was successfully applied to these problems achieving state-of-the-art performances.
Introduction
The most popular way to transform a set of low-level local features extracted from an image into a high-level image representation is the bag-of-visual-words (BOV) [1,2] inspired by the traditional bag-of-words for text analysis. The Fisher Vector representation of images can be seen as an extension of this representation. Both the FV and BOV are based on an intermediate representation, the visual vocabulary built in the low level feature space. Then a variable size set of low level feature is transformed into a fixed sized image representation (signature). When the visual vocabulary is learnt in an unsupervised manner on a set of features from the image database (called universal vocabulary), these representations have the main advantage to be class independent. This latter property allows their usage both in supervised (categorization, semantic image segmentation) and unsupervised tasks (clustering, retrieval). The focus of this paper being classification and retrieval, we briefly review these two fields.
Image Classification. Image categorization is the problem which consists in assigning one or multiple labels to an image based on its semantic content. This is a very challenging task as one has to cope with inherent object/scene variations as well as changes in viewpoint, lighting and occlusion. Hence, although much progress has been made in the past few years, image categorization remains an open problem. The most popular approach to image classification is to describe images with a bag-of-visual-words (BOV) histograms and to classify them using non-linear Support Vector Machines (SVM) [2]. Several variants and extensions were proposed to the original approach. The most common trend is to use a combination of a set of different patch detectors, local descriptors and spatial pyramids, then to train generally non-linear classifiers on the corresponding high-level descriptors and finally, to combine the output of the classifiers [3-6]. Systems following this paradigm have consistently performed among the best in the successive PASCAL VOC evaluations [7]. However, an important limitation of such approaches is their scalability to large quantities of training images.
To overcome this limitation, recently, several algorithms have been proposed to reduce the training cost of the training using approximations for additive kernels [8-11]. These algorithms scale linearly with the number of training samples while providing the same accuracy as the original non-linear SVM classifiers. On the other hand, rather than modifying the classifiers, attempts have been made to obtain BOV representations which perform well with linear classifiers. Indeed, Yang et al. [12] using the sparse coding with a max-pooling of the descriptor-level statistics obtained excellent classification results. The FV [13, 14] is an other alternative representation of images that performs well with linear classifiers as we will show in the section 3.
Image Retrieval. As we mentioned above, the FV is a class independent image representation, hence can be seen as an image signature. While most commercial image retrieval systems are still based on textual search (Google images, Getty images, Flickr), huge steps were made on content based image retrieval in the last decade. While early systems were mainly used global image descriptors [15], recent systems extract rather local features from image patches or segmented image regions and use techniques based on feature matching [16], build inverted files [17], bag-of visual words [1] or Fisher Vectors [18]. In order to cope with the increasing amount and the diversity of images in the image databases, there were also several attempts to propose methods that scale well with the number of images. On of the inconvenience of the BOV and FV representations is the size of the signature. Therefore, On one hand [19] proposes a compression methods applied to BOV where a random aggregation of visual words precedes standard compression techniques such as Local Sensitive Hashing (LSH). On other hand, [20] decomposes an image into three layers: background information (which is discarded), information related to a set of pre-learned topics (which is dense and can be compressed with LSH) and residual information (which can be encoded in a sparse manner). In contrast to them, Perronnin et al. proposes a compression method on Fisher Vectors showing excellent performance even with very highly compressed representations [18].
As images are often accompanied by text, metadata, a lot research work focused also on the information fusion and multi-modal retrieval systems. For example, the aim of ImageClef Evaluation Forum (http://www.imageclef.org/) is to allow a fair comparison of different such multi-modal (mainly image and text based) retrieval systems through different tasks (photo retrieval, medical image retrieval) [21]. We will show in section 4 that when we appropriately combine the FV based visual retrieval with textual retrieval, the accuracy of both mono-modal systems are significantly boosted.
The rest of the paper is organized as follows. First we described the BOV and Fisher Vector image representations in section 2. In section 3 we show several image categorization experiments and in section 4 we show image retrieval experiments. In section 5 we describe some further applications of the FVs and finally we conclude in section 6.
Image Representations
In this section we first briefly recall the soft BOV representation using a generative model for to visual vocabulary. We then show how to build corresponding Fisher Vectors (FV). Finally, we show a simple compress method for them.
Soft BOV. The bag-of-visual words (BOV) image representation is based on an intermediate representation: the visual vocabulary. In the case of a generative approach, the visual vocabulary is a probability density function (pdf) – denoted by p – which models the emission of the low-level descriptors in the image. We model the visual vocabulary with a Gaussian mixture model (GMM) where each Gaussian corresponds to a visual word [22, 23].
Let![]() be the set of parameters of p where Wi, μi and Σι denote respectively the weight, mean vector and covariance matrix of Gaussian i and N is the number of Gaussians. Let Pi be the distribution of Gaussian i so that we have:
be the set of parameters of p where Wi, μi and Σι denote respectively the weight, mean vector and covariance matrix of Gaussian i and N is the number of Gaussians. Let Pi be the distribution of Gaussian i so that we have:
Let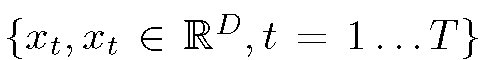 be the set of ^-dimensional local descriptors of the image I generated by the Gaussian Mixture Model (GMM) with parameters λ. We denote by
be the set of ^-dimensional local descriptors of the image I generated by the Gaussian Mixture Model (GMM) with parameters λ. We denote by![]() the probability that the low-level descriptor xt is assigned to Gaussian i. Using Bayes’ formula, we have:
the probability that the low-level descriptor xt is assigned to Gaussian i. Using Bayes’ formula, we have:
In the BOV representation, the low-level descriptor xt is hence transformed into the high-level N-dimensional descriptor:
where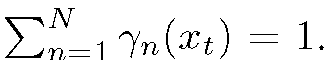 The image-level BOV is then simply acumulation of these probabilities over all low level descriptors:
The image-level BOV is then simply acumulation of these probabilities over all low level descriptors:
We call this representation soft BOV, as instead of assigning an image descriptor to a single word (here Gaussian) we assign it to all Gaussians with a given probability.
A classical BOV (one descriptor assigned to a single visual word) can be seen as a particular case, where instead of using the soft assignements (3), the coordinates of Yt are:
The Fisher Vector (FV). The Fisher Vector(FV) [13, 24] is an extension of the BOV representation. Instead of characterizing an image by the number of occurrences of each visual word, it is characterized by a gradient vector derived from a generative probabilistic model. The gradient of the log-likelihood describes the contribution of the parameters to the generation process.
Assuming again that the local descriptors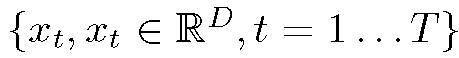 of an image are generated independently by the Gaussian mixture model with parameters λ, we can characterize I by the following gradient vector [13, 24]:
of an image are generated independently by the Gaussian mixture model with parameters λ, we can characterize I by the following gradient vector [13, 24]:
To compare two images I and J, a natural kernel on these gradients is the Fisher Kernel [24]:
where Fx is the Fisher Information Matrix:
As![]() is symmetric and positive definite,
is symmetric and positive definite,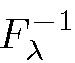 has a Cholesky decomposition
has a Cholesky decomposition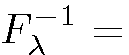
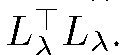 Therefore K (I, J) can be rewritten as a dot-product between normalized vectors
Therefore K (I, J) can be rewritten as a dot-product between normalized vectors![]() We will refer to
We will refer to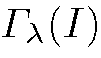 as the Fisher Vector (FV) of the image I.
as the Fisher Vector (FV) of the image I.
As it was shown in [13] that the gradient with respect to the weights Wi generally bring little additional information, we consider only the gradients with respect to the mean and standard deviation parameters. We assume diagonal covariance matrices and denote diag Hence, we can make use of the diagonal closed-form approximation of Fx proposed in [13], in which case the normalization of the gradient by
Hence, we can make use of the diagonal closed-form approximation of Fx proposed in [13], in which case the normalization of the gradient by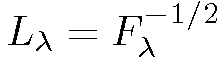 becomes simply a whitening of the dimensions.
becomes simply a whitening of the dimensions.
Hence, we have the following formulas for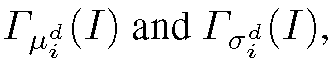 respectively the nor- malizeed gradient with respect to mean
respectively the nor- malizeed gradient with respect to mean![]() and standard deviation
and standard deviation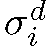 (see also [14]):
(see also [14]):
Fig. 1. Distribution of the values in the first dimension of the Fisher Vector obtained with 256 Gaussians (a) with no power normalization. (d) with a = 0.5 power normalization. Both histograms have been estimated on the 5,011 training images of the PASCAL VOC 2007 dataset [7].
The final gradient vector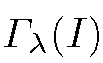 is then the concatenation of all
is then the concatenation of all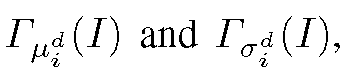 where i = 1 …N. Hence the FV is M-dimensional with M = 2ND.
where i = 1 …N. Hence the FV is M-dimensional with M = 2ND.
The Fisher Vector has several advantages over the BOV. As it is not limited to the number of occurrences of each visual word but it also encodes additional information about the distribution of the descriptors for the same vocabulary size, it is much larger. Since the size of the visual vocabulary determines largely the cost of their computation, the computational cost of the FV is significantly lower than of an equivalent size BOV. As the FV encodes richer information, as we will there is no need to use costly kernels but the linear kernel is sufficient. Consequently, the cost of the corresponding categorization or retrieval system can also be kept low and hence easily scalable.
The main motivation of the power normalization is to make the distribution of the features in a given dimension m less peaky around zero (see e.g. Figure 1). As suggested in [14], we use a component-wise power normalization with a = 0.5:
It has been shown that the Fisher Vector approximately discards image-independent (i.e. background) information [14]. However the vector depends on the proportion of image-specific information w.r.t. to the proportion of background information. We use therefore the L2 normalization to cancel this effect.
Compressed Binary Fisher Vectors. Storage/memory cost for image signatures when large image databases are considered becomes a real issue. The FV as presented above is in general of large size. In order to reduce the image signature size, Perronnin et al. [18] proposed a simple method to easily compressed the Fisher Vector. It basically consist in power normalization of the FV with a power value a = 0. Hence, as a goes to zero, the α-normalized Fisher Vector converges to a ternary representation1. This ternary encoding can be turned into an equivalent binary encoding which is more efficient both in terms of storage and computation [18]. To do this we can decompose the equation (9) as follows:
Fig. 2. Generic Visual Categorization (GVC) – pipeline
Note that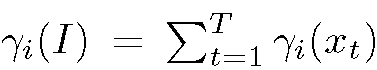 is the proportion of descriptors of X soft-assigned to the word (Gaussian) i, (see (4)). The first part bi of (11) is independent of the low level dimension d and is positive or zero2. Hence we can encode it as bi(I) = 1 if Yi(I) > 0 and 0 otherwise. The second part, Sf (I) can take positive and negative values, so a natural binary coding for this is using the sign function. Therefore, the binarized Fisher Vector can be encoded on N + ND bits. The similarity between two binary representations is:
is the proportion of descriptors of X soft-assigned to the word (Gaussian) i, (see (4)). The first part bi of (11) is independent of the low level dimension d and is positive or zero2. Hence we can encode it as bi(I) = 1 if Yi(I) > 0 and 0 otherwise. The second part, Sf (I) can take positive and negative values, so a natural binary coding for this is using the sign function. Therefore, the binarized Fisher Vector can be encoded on N + ND bits. The similarity between two binary representations is:
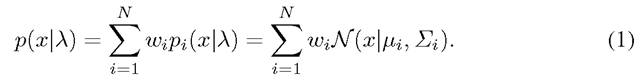
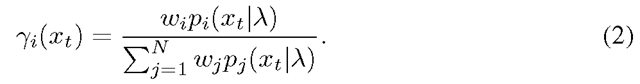
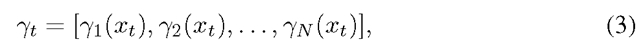
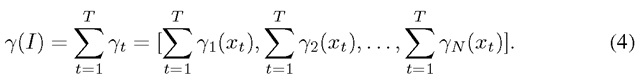
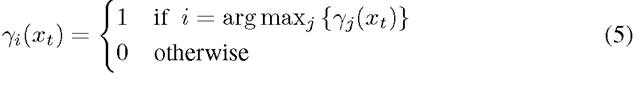
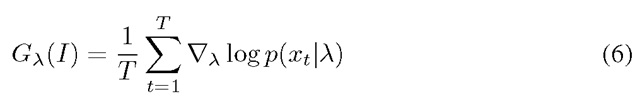
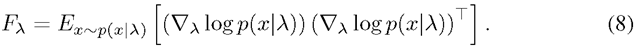
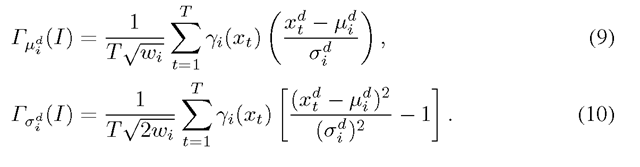
![Distribution of the values in the first dimension of the Fisher Vector obtained with 256 Gaussians (a) with no power normalization. (d) with a = 0.5 power normalization. Both histograms have been estimated on the 5,011 training images of the PASCAL VOC 2007 dataset [7]. Distribution of the values in the first dimension of the Fisher Vector obtained with 256 Gaussians (a) with no power normalization. (d) with a = 0.5 power normalization. Both histograms have been estimated on the 5,011 training images of the PASCAL VOC 2007 dataset [7].](http://what-when-how.com/wp-content/uploads/2012/06/tmp583964_thumb.png)