Scene Statistics and 3D Surface Perception (Computer Vision) Part 2

Implications toward depth inference

Armed with a better understanding of the statistics of real scenes, we are better prepared to develop successful depth inference algorithms. One example is range image superresolution. Often, we may have a high-resolution color image of a scene but only a low spatial resolution range image (range images record the 3D distance between the scene and the camera for each pixel). This often happens if our range image was acquired by applying a stereo depth inference algorithm. Stereo algorithms rely on smoothness constraints, either explicitly or implicitly, and so the high-frequency components of the resulting range image are not reliable (Cryer et al., 1995; Scharstein and Szeliski, 2002). Laser range scanners are another common source of low-resolution range data. Laser range scanners typically acquire each pixel sequentially, taking up to several minutes for a high-resolution scan. These slow scan times can be impractical in real situations, so in many cases, only sparse range data are available. In other situations, inexpensive scanners are used that can capture only sparse depth values.

It should be possible to improve our estimate of the high spatial frequencies of the range image by using monocular cues from the high-resolution intensity (or color) image. One recent study suggested an approach to this problem known as shape recipes (Freeman and Torralba, 2003; Torralba and Freeman, 2003). The basic principle of shape recipes is that a relationship between shape and appearance could be learned from the low-resolu-tion image pair, and then extrapolated and applied to the high-resolution intensity image to infer the high spatial frequencies of the range image. One advantage of this approach is that hidden variables important to inference from monocular cues, such as illumination direction and material reflectance properties, might be implicitly learned from the low-reso-lution range and intensity images.

From our statistical study, we now know that fine details in K = ZI*/II* do not generalize across scales, as was assumed by shape recipes. However, the coarse structure of K roughly follows a 1/r power law. We can exploit this statistical trend directly. We can simply estimate BK(6) using the low-resolution range image, use the 1/r power law to extrapolate K ~ BK(6)/r into the higher spatial frequencies, and then use this estimate of K to reconstruct the high-frequency range data. Specifically, from the low-resolution range and intensity image, we compute low-resolution spectra of ZI* and II*. From the highest frequency octave of the low-resolution images, we estimate Bn(6) and BZI(6). Any standard interpolation method will work to estimate these functions. We chose a cos3(6 + n^/4) basis function based on steerable filters (Adelson and Freeman, 1991). We now can estimate the high spatial frequencies of the range image, z. Define

where Flow is the low-pass filter that filters out the high spatial frequencies of z where depth information is either unreliable or missing.

Because our model is derived from scene statistics and avoids some of the mistaken assumptions in the original shape recipe model, our extension provides a twofold improvement over Freeman and Torralba’s original approach (2003), while using far fewer parameters. Figure 1.5 shows an example of the output of the algorithm.

This power law-based approach can be viewed as a statistically informed generalization of a popular shape-from-shading algorithm known as linear shape from shading (Pentland, 1990), which remains popular due to its high efficiency. Linear shape from shading attempts to reconstruct 3D shape from a single image using Equation (1.5) alone, ignoring shadow cues and the da Vinci correlation. As mentioned previously, the da Vinci correlation is a product of cast shadows, complex 3D surfaces, diffuse lighting, and lighting interreflections. All four of these image formation phenomena are exceptionally cumbersome to invert in a deterministic image formation model, and subsequently, they have been ignored by most previous depth inference algorithms. However, taken together, these phenomena produce a simple statistical relationship that can be exploited using highly efficient linear algorithms such as Equation 1.7. It was not until the statistics of natural range and intensity images were studied empirically that the strength of these statistical cues was made clear.

Figure 1.5 (a) An example intensity image from our database. (b) A computer-generated Lambertian rendering of the corresponding laser-acquired low-resolution range image. This figure shows the low-resolution range image that, for purposes of illustration, has been artificially rendered as an image. Note the oversmoothed edges and lack of fine spatial details that result from the downsampling. (c) Power-law method of inferring high-resolution three-dimensional (3D) shape from a low-resolution range image and a high-resolution color image. High spatial-frequency details of the 3D shape have been inferred from the intensity image (left). Notice that some high-resolution details, such as the cross in the sail, are not present in the low-resolution range image but were inferred from the full-resolution intensity image.

The power-law algorithm described here presents a new opportunity to test the usefulness of the da Vinci shadow cues, by comparing the power-law algorithm results to the linear shape-from-shading technique (Pentland, 1990). When our algorithm was made to use only shading cues (by setting the real part of Kpowerlaw(r, 6) to zero), the effectiveness of the algorithm was reduced to 27% of its original performance. When only shadow cues were used (by setting the imaginary part of Kpowerlaw(r, 6) to zero), the algorithm retained 72% of its original effectiveness (Potetz and Lee, 2006). Thus, in natural scenes, linear shadow cues proved to be significantly more powerful than linear shading cues. These results show that shadow cues are far more useful than was previously expected. This is an important empirical observation, as shape from shading has received vastly more attention in computer vision research than shape from shadow. This finding highlights the importance of shadow cues and the benefits of statistical studies of natural scenes.

As expected given the analysis of the da Vinci correlation above, the relative performance of shadow and shading cues depends strongly on the category of the images considered. Shadow cues were responsible for 96% of algorithm performance in foliage scenes, 76% in scenes of rocky terrain, and 35% in urban scenes.

Statistical Inference for Depth Inference

The approach described above shows the limits of what is possible using only second-order linear statistics. The study of these simple models is important, because it helps us to understand the statistical relationships that exist between shape and appearance. However, simple linear systems capture only a fraction of what is achievable using a complete statistical inference framework. The problem of inferring a 3D shape from image cues is both highly complex and highly underconstrained: for any given 2D image, there are countless plausible 3D interpretations of that scene. Our goal is to find solutions that are especially likely. Powerful statistical methods will be necessary to achieve these goals. In this section, we discuss the use of modern statistical inference techniques for inferring a 3D shape from images.

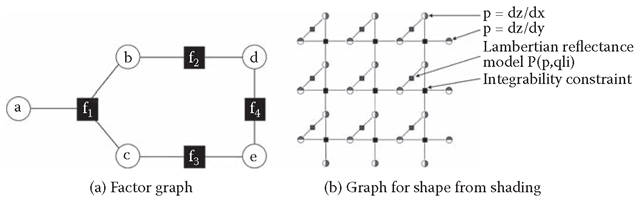
In recent years, there has been a great deal of progress made in computer vision using graphical models of large joint probability distributions (Fei-Fei and Perona, 2005; Freeman et al., 2000; Sun et al., 2003; Tang et al., 2005; Torralba et al., 2003; Zhu and Tu, 2002). Graphical models offer a powerful framework to incorporate rich statistical cues from natural scenes and can be applied directly to the problem of depth inference. Bayesian inference of shape (depth) Z from images I involves estimating properties of the posterior distribution P(Z | I). The dimensionality of the posterior distribution P(Z | I), however, is far too great to model directly. An important observation relevant to vision is that the interdependency of variables tends to be relatively local. This allows the factorization of the joint distribution into a product of “potential functions,” each of lower dimensionality than the original distribution (as shown in Figure 1.6). In other words,

where xa is some subset of variables in I and Z. Such a factorization defines an example of a graphical model known as a “factor graph”: a bipartite graph with a set of variable nodes (one for each random variable in the multivariate distribution) and a set of factor nodes (one for each potential function). Each factor node is connected to each variable referenced by its corresponding potential function. (See Figure 1.6 for an example, or reference (Frey, 1998) for a review of factor graphs.) Factor graphs that satisfy certain constraints can be expressed as Bayes networks, or for other constraints, as Markov random fields (MRFs). Thus, these approaches are intimately connected and are equivalent in terms of neural plausibility.

FIGURE 1.6 (a) An example factor graph. This graph represents the factorization of a joint probability distribution over five random variables: P(a, b, c, d, e) ^ f1(a, b, c)f2(b, d)f3(c, e)f4(d, e)). (b) A factor graph to solve the classical Lambertian shape-from-shading problem using linear constraint nodes. The representation of a three-dimensional (3D) shape is twice overcomplete, including p and q slope values at each pixel. The linear constraint nodes are shown as black squares, and they enforce the consistency (integrability) of the solution. The gray squares represent factor nodes encoding the reflectance function.

Exact inference on factor graphs is possible only for a small subclass of problems. In most cases, approximate methods must be used. There are a variety of existing approaches to approximate the mode of the posterior distribution (MAP, or maximum a posteriori) or its mean (MMSE, or minimum mean-squared error), such as Markov chain Monte Carlo (MCMC) sampling, graph cuts, and belief propagation. In this section, we explore the use of the belief propagation algorithm. Belief propagation is advantageous in that it imposes fewer restrictions on the potential functions than graph cuts (Kolmogorov and Zabih, 2001) and is faster than MCMC. Belief propagation is also interesting in that it is highly neurally plausible (Lee and Mumford, 2003; Rao, 2004) and has been advanced as a possible model for statistical inference in the brain (Pearl, 1988).

Belief propagation has been applied successfully to a wide variety of computer vision problems (Freeman et al., 2000; Potetz, 2007; Sun et al., 2003; Tang et al., 2005) and has shown impressive empirical results on a number of other problems (Frey and Dueck, 2007; Kschischang and Frey, 1998). Initially, the reasons behind the success of belief propagation were only understood for those cases where the underlying graphical model did not contain loops. The many empirical successes on graphical models that did contain loops were largely unexplained. However, recent discoveries have provided a solid theoretical justification for “loopy” belief propagation by showing that when belief propagation converges, it computes a minima of a measure used in statistical physics known as the Bethe free energy (Yedidia et al., 2000). The Bethe free energy is based on a principled approximation of the KL-divergence between a graphical model and a set of marginals and has been instrumental in studying the behaviors of large systems of interacting particles, such as spin glasses. The connection to Bethe free energy had an additional benefit in that it inspired the development of algorithms that minimize the Bethe free energy directly, resulting in variants of belief propagation that guarantee convergence (Heskes et al., 2003; Yuille, 2002), improve performance (Yedidia et al., 2000, 2003), or in some cases, guarantee that belief propagation computes the globally optimal MAP point of a distribution (Weiss and Freeman, 2007).

Belief propagation estimates the marginals bt ( xt ) = XX\x.P( X ) by iteratively computing messages a long each edge of the graph according to the following equations:

where f and g are factor nodes, i and j are variable nodes, and N (i) is the set of neighbors of node i (Heskes, 2004). Here, bi (xi) is the estimated marginal ofvari-able i. Note that the expected value of X or equivalently, the minimum mean-squared error (MMSE) point estimate, can be computed by finding the mean of each marginal. If the most likely value of X is desired, also known as the maximum a posteriori (MAP) point estimate, then the integrals of Equation (1.10) are replaced by suprema. This is known as max-product belief propagation.

For many computer vision problems, belief propagation is prohibitively slow. The computation of Equation (1.10) has a complexity of O(MN), where M is the number of possible labels for each variable, and N is the number of neighbors of factor node f In many computer vision problems, variables are continuous or have many labels. In these cases, applications of belief propagation have nearly always been restricted to pairwise connected MRFs, where each potential function depends on only two variable nodes (i.e., N = 2) (Freeman et al., 2000; Sun et al., 2003). However, pairwise connected models are often insufficient to capture the full complexity of the joint distribution and thus would severely limit the expressive power of factor graphs. Developing efficient methods for computing nonpairwise belief propagation messages over continuous random variables is therefore crucial for solving complex problems with rich, higher-order statistical distributions encountered in computer vision.

In the case that the potential function ÿ can be expressed in terms of a weighted sum of its inputs, we developed a set of techniques to speed up the computation of messages considerably. For example, suppose the random variables a, b, c, and d are all variable nodes in our factor graph, and we want to constrain them such that a + b = c + d. We would add a factor node f connected to all four variables with potential function

To compute we use Equation 1.10:

where x = a + b and y = a + b – c. Notice that in Equation (1.16), the second summand (in parentheses) does not depend on a. This summand can be computed in advance by summing over y for each value of x. Thus, computingusing Equation (1.16) is O (M2), which is far superior to a straightforward computation of Equation (1.13), which is O(M4). In (Potetz and Lee, 2008), we show how this approach can be used to compute messages in time O (M2) for all potential functions of the form

This reduces a problem from exponential time to linear time with respect to the number of variables connected to a factor node. Potentials of this form are common in graphical models, in part because they offer advantages in training graphical models from real data (Friedman et al., 1984; Hinton, 1999; Roth and Black, 2005; Zhu et al., 1998).

This approach reduces a problem from exponential time to linear time with respect to the number of variables connected to a factor node. With this efficient algorithm, we were able to apply belief propagation to the classical computer vision problem of shape from shading, using the factor graph shown in Figure 1.6 (see Potetz, 2007 for details). Previously, the general problem of shape from shading was solved using gradient descent-based techniques. In complex, highly nonlinear problems like shape from shading, these approaches often become stuck inside local, suboptimal minima. Belief propagation helps to avoid difficulties with local minima in part because it operates over whole probability distributions. Gradient descent approaches maintain only a single 3D shape at a time, iteratively refining that shape over time. Belief propagation seeks to optimize the single-variate marginals bi (xi) for each variable in the factor graph.

Solving shape from shading using belief propagation performs significantly better than previous state-of-the-art techniques (see Figure 1.7). Note that without the efficient techniques described here, belief propagation would be intractable for this problem, requiring over 100,000 times longer to compute each iteration. In addition to improved performance, solving shape from shading using belief propagation allows us to relax many of the restrictions typically assumed by shape-from-shading algorithms in order to make the problem tractable. The classical definition of the shape-from-shading problem specifies that lighting must originate from a single point source, that surfaces should be entirely matte, or Lambertian in reflectance, and that no markings or colorations can be present on any surface. The flexibility of the belief propagation approach allows us to start relaxing these constraints, making shape from shading viable in more realistic scenarios.

FIGURE 1.7 Comparison between our results of inferring shape from shading using loopy belief propagation (row b) with previous approaches (rows c and d). Each row contains a three-dimensional (3D) wire mesh plot of the surface (right) and a rendering (left) of that surface under a light source at location (1,0,1). (a) The original surface. The rendering in this column serves as the input to the shape from shading (SFS) algorithms in the next three columns. (b) The surface recovered using our linear constraint node approach. (c) The surface recovered using the method described by Lee and Kuo (1993). This algorithm performed best of the six SFS algorithms reviewed in a survey paper by Zhang et al. (1999). (d) The surface recovered using the method described by Zheng and Chellappa (1991). Our approach (row b) offers a significant improvement over previous leading methods. It is especially important that rerendering that recovered surface very closely resembles the original input image. This means that the Lambertian constraint at each pixel was satisfied, and that any error between the original and recovered surface is primarily the fault of the simplistic model of prior probability of natural 3D shapes used here.

Concluding remarks and future directions

The findings described here emphasize the importance of studying the statistics of natural scenes; specifically, it is important to study not only the statistics of images alone, but images together with their underlying scene properties. Just as the statistics of natural images has proven invaluable for understanding efficient image coding, transmission, and representation, the joint statistics of natural scenes stands to greatly advance our understanding of perceptual inference. The discovery of the da Vinci correlation described here illustrates this point. This absolute correlation between nearness and brightness observed in natural 3D scenes is among the simplest statistical relationships possible. However, it stems from the most complex phenomena of image formation; phenomena that have historically been ignored by computer vision approaches to depth inference for the sake of mathematical tractability. It is difficult to anticipate this statistical trend by only studying the physics of light and image formation. Also, because the da Vinci correlation depends on intrinsic scene properties such as the roughness or complexity of a 3D scene, physical models of image formation are unable to estimate the strength of this cue, or its prevalence in real scenes. By taking explicit measurements using laser range finders, we demonstrated that this cue is very strong in natural scenes, even under oblique, nondiffuse lighting conditions. Further, we showed that for linear depth inference algorithms, shadow cues such as the da Vinci correlation are 2.7 times as informative as shading cues in a diverse collection of natural scenes. This result is especially significant, because depth cues from shading have received far more attention than shadow cues. We believe that continued investigation into natural scene statistics will continue to uncover important new insights into visual perception that are unavailable to approaches based on physical models alone.

Another conclusion we wish to draw is the benefit of statistical methods of inference for visual perception. The problem of shape from shading described above was first studied in the 1920s in order to reconstruct the 3D shapes of lunar terrains (Horn, 1989). Since that time, approaches to shape from shading were primarily deterministic and typically involved iteratively refining a single shape hypothesis until convergence was reached. By developing and applying efficient statistical inference techniques that consider distributions over 3D shapes, we were able to advance the state of shape from shading considerably.

The efficient belief propagation techniques we developed have similar applications in a variety of perceptual inference tasks. These and other statistical inference techniques promise to significantly advance the state of the art in computer vision and to improve our understanding of perceptual inference in general.

In addition to improved performance, the approach to shape from shading described above offers a new degree of flexibility that should allow shading to be exploited in more general and realistic scenarios. Previous approaches to shape from shading typically relied heavily on the exact nature of the Lambertian reflectance equations, and so could only be applied to surfaces with specific (i.e., matte) reflectance qualities with no surface markings. Also, specific lighting conditions were assumed. The approach described above applies directly to a statistical model of the relationship between shape and shading, and so it does not depend on the exact nature of the Lambertian equation or specific lighting arrangements. Also, the efficient higher-order belief propagation techniques described here make it possible to exploit stronger, nonpairwise models of the prior probability of 3D shapes. Because the problem of depth inference is so highly underconstrained, and natural images admit large numbers of plausible 3D interpretations, it is crucial to utilize an accurate model of the prior probability of 3D surface. Knowing what 3D shapes commonly occur in nature and what shapes are a priori unlikely or odd is a very important constraint for depth inference. Finally, the factor graph representation of the shape-from-shading problem (see Figure 1.6) can be generalized naturally to exploit other depth cues, such as occlusion contours, texture, perspective, or the da Vinci correlation and shadow cues. The state-of-the-art approaches to the inference of depth from binocular stereo pairs typically employ belief propagation over a MRF. These approaches can be combined with our shape-from-shading framework in a fairly straightforward way, allowing both shading and stereo cues to be simultaneously utilized in a statistically optimal way. Statistical approaches to depth inference make it possible to work toward a more unified and robust depth inference framework, which is likely to become a major area of future vision research.