3D Surface Representation Using Ricci Flow (Computer Vision) Part 4

Applications

The 3D surface conformal representation using Ricci flow has broad applications.

Conformal Brain Mapping

In medical imaging, it is helpful to compare different cortex surfaces for monitoring the progress of neurological diseases or for diagnosing the potential abnormality.

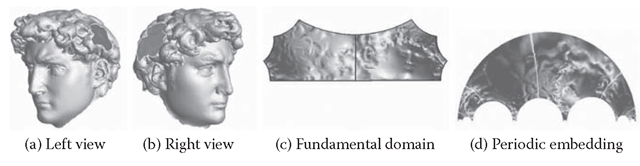
FIGURE 4.10 Hyperbolic Yamabe flow for surface with negative Euler number. (a) and (b) The left and right views of a genus zero surface with 3 boundaries. (c) The fundamental domain on the hyperbolic space H2. (d) The periodic conformal embedding on H2.

FIGURE 4.11 Conformal brain mapping. (a) A brain cortex surface, which is a topological sphere. (b) The spherical conformal mapping of (a) onto the unit sphere.

Human brain cortex surfaces are highly convoluted. It is difficult to compare the shapes of two cortical surfaces directly. By using conformal shape representation, we can map brain surfaces to the unit sphere and compare their spherical images easily. By measuring the difference between their conformal factor and mean curvature functions, the distance between the shapes can be measured quantitatively. Figure 4.11 shows an example of such conformal brain mapping. Details can be found in Gu et al. (2004).

There are prominent biological features on brain cortical surfaces. In the brain surface matching process, we can enforce the alignment of these landmarks in the following way. As shown in Figure 4.12, the cortex surface is sliced open along the landmarks and then mapped to the canonical disk with circular holes. During the matching, the corresponding boundaries are aligned together. This guarantees the matching between the corresponding landmarks.

Surface Matching

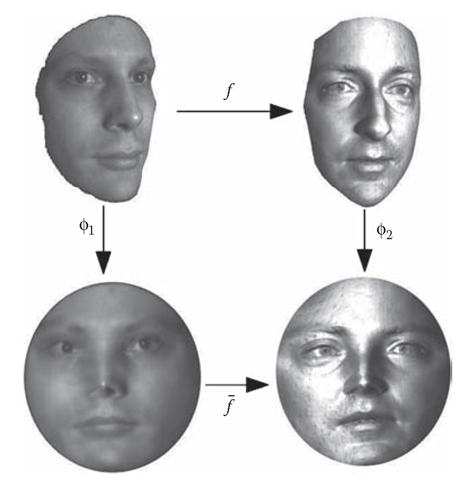
Given two surfaces S1, S2 embedded in M3, we want to find a good matching f : S1 ^ S2, which minimizes the distortion between them. It is generally difficult to match the surfaces directly in M3. As shown in Figure 4.13, we compute two conformal mappings $ : St ^ D,i = 1,2, D is the canonical unit disk. Then we can find a mapping f : D ^ D, which inducesf:

FIGURE 4.12 Conformal brain mapping with landmarks. (a) A brain cortex surface with landmarks, which is a genus zero surface with boundaries. (b) The circular conformal mapping of (a) onto the unit disk.

For example, if we requirefto be isometric, then the corresponding f satisfies the following constraints: f must be conformal, and f must satisfy the following equation:

whereare the conformal factors of respectively.

FIGURE 4.13 Surface matching using conformal geometry.

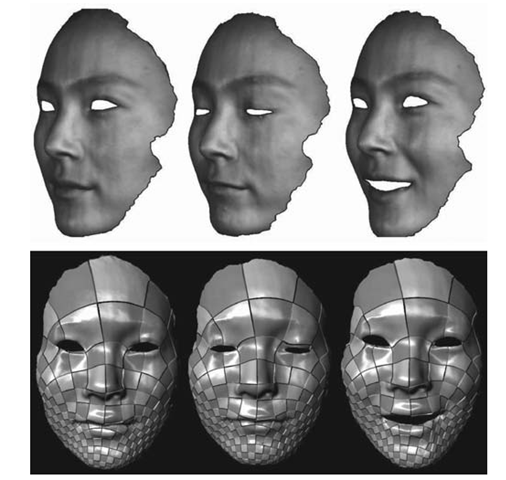
FIGURE 4.14 Surface matching using conformal geometry.

Figure 4.14 shows a matching result for a 3D human face with different expressions. The matching result is illustrated by consistent texture mapping. Details can be found in Zeng et al. (2008).

Teichmüller Shape Space

Surfaces with the same topology can be classified according to their con-formal structures. Two surfaces are conformally equivalent, if there exists a conformal mapping between them. The space of all conformal equivalence classes is called the Teichmüller space. According to Teichmüller theory, the Teichmüller space is also a finite dimensional Riemannian manifold.

All genus zero closed surfaces are conformally equivalent to the unit sphere; therefore, the Teichmüller space of genus zero closed surfaces has a single point. The dimension of genus one closed surfaces is two. The dimension of genus g closed surfaces is 6g – 6.

Given a surface in M3, the Teichmüller coordinates can be computed using the Ricci flow. The coordinates can be used for shape classification and indexing. For example, Figure 4.15 shows the Teichmüller shape space of genus zero surfaces with three boundaries. First, we compute the hyperbolic metric using Ricci flow, such that the boundaries become geodesics. The lengths of three boundaries under the hyperbolic form the Teichmüller coordinates.

FIGURE 4.15 Teichmüller space of genus zero surface with three boundaries.

The method can be generalized to high genus surfaces as shown in Figure 4.16. First, the hyperbolic metric is computed using Ricci flow, which is conformal to the original induced Euclidean metric. Then, there exists a unique geodesic in each homotopy class in the fundamental group. The geodesic lengths form a spectrum, which can be used as the coordinates in the Teichmüller space. Details can be found in Jin et al. (2008).

FIGURE 4.16 The geodesic spectrum under hyperbolic metric can be used to classify high genus surfaces.

Conclusion

This work proposes a rigorous and general framework for representing 3D surfaces with arbitrary topologies in 3D Euclidean space. The geometric information of a surface is decomposed to four layers—topology, conformal structure, Riemannian metric, and mean curvature—that together determine the surface unique up to a rigid motion.

Ricci curvature flow is the essential tool to compute the surface representation. This work presents discrete curvature flow methods that are recently introduced into the engineering fields: the discrete Ricci flow and discrete Yamabe flow for surfaces. Applications for brain mapping, surface matching, and Teichmüller shape space are briefly explained.