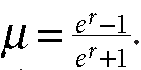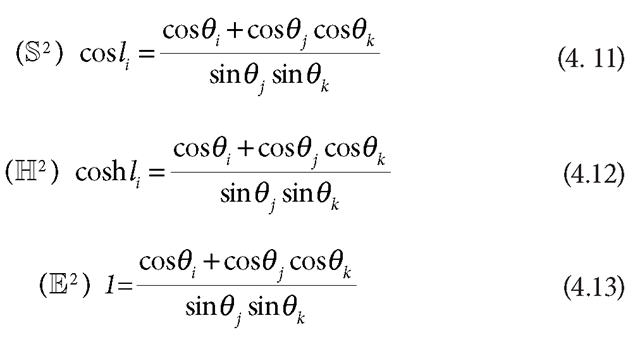Introduction
3D Surface Representation
Three-dimensional (3D) surface representation plays a fundamental role in middle-level vision. In this work, a representation of 3D surfaces based on modern geometry is introduced. According to Felix Klein’s Erlangen program, different geometries study the invariants under different transformation groups.
Given a surface embedded in 3D Euclidean space, S M3, intrinsically, the surface has four layers of geometric information: topology, con-formal structure, Riemannian metric, and embedding, corresponding to four geometries: topology, conformal geometry, Riemannian geometry, and differential geometry for surfaces in M3. In order to represent the topology, genus and the number of boundaries are required; for con-formal geometry, 6g – 6 (or two) parameters are needed to describe the conformal structure of a genus g > 1 surface (or a torus). All genus zero closed surfaces have the same conformal structure. Given the conformal structure of S, a canonical conformal domain of S can be uniquely determined, denoted as DS; for Riemannian geometry, a function defined on the conformal domain XS : DS ^ M is needed to specify the Riemannian metric; and finally, by adding a mean curvature function Hs : Ds M, the embedding of S in M3 can be determined unique up to a rigid motion. Therefore, in order to represent a 3D surface, one needs a finite number of parameters to determine a canonical domain DS, then two functions X,H defined on the domain. We denote this representation as (DS ,XS, HS ), and call it conformal representation.
Converting a surface S to its conformai representation (DS ,XS, HS ) is a challenging problem. Ricci curvature flow offers a powerful tool for computing it.
Ricci Curvature Flow
Intrinsic curvature flows have been used in Riemannian geometry in the past 50 years with great success. One of the most recent examples appears in the proof of the Poincaré conjecture on two manifolds (Perelman, 2002, 2003a, 2003b), where the Ricci flow is employed as a fundamental tool.
These flows deform a given Riemannian metric according to its curvature. Among the most famous ones are the Ricci flow and the Yamabe flow. Both can be used to design Riemannian metrics with special curvature properties.
The Ricci flow deforms the Riemannian metric according to its Ricci curvature. In particular, it can be used to find a metric with constant Ricci curvature. There is a simple physical intuition behind it. Given a compact manifold with a Riemannian metric, the metric induces the curvature function. If the metric is changed, the curvature will be changed accordingly. The metric can be deformed in the following way: at each point, locally scale the metric, so that the scaling factor is proportional to the curvature at the point. After the deformation, the curvature will be changed. Repeating this deformation process, both the metric and the curvature will evolve like heat diffusion. Eventually, the curvature function will become constant everywhere.
Another intrinsic curvature flow is called Yamabe flow. It has the same physical intuition with the Ricci flow, except for the fact that it is driven by the scalar curvature instead of Ricci curvature. For two manifolds, the Yamabe flow is essentially equivalent to the Ricci flow. But for higherdimensional manifolds, Yamabe flow is much more flexible than the Ricci flow to reach constant-scalar-curvature metrics.
Due to the ability of intrinsic curvature flows on metric designs, two curvature flows have been recently introduced into the engineering fields: a discrete Ricci flow on surfaces and a discrete Yamabe flow on surfaces. Through these works, the power of curvature flows has been extended from pure theoretical study to solving practical problems.
One should note that in engineering fields, manifolds are usually approximated using discrete constructions, such as piecewise linear meshes; in order to employ curvature flow to solve practical problems, we need to extend the theories of curvature flows from the smooth setting to the corresponding discrete setting, and we need to pay attention to the convergence of the latter to the former. Based on the discrete theories and formula, one is allowed to design computer algorithms that can simulate and compute the flow.
A Brief History
The theory of intrinsic curvature flows originated from differential geometry and was later introduced into the engineering fields. In this section, we give a brief overview of the literature that is directly related to the two flows mentioned above. For each flow, we would introduce some representative work on two aspects: theories in the smooth setting and the discrete setting.
Ricci Flow on Surfaces
The Ricci flow was introduced by Richard Hamilton in a seminal paper (1982) for Riemannian manifolds of any dimension. The Ricci flow has revolutionized the study of geometry of surfaces and three-manifolds and has inspired huge research activities in geometry. In particular, it leads to a proof of the 3D Poincaré conjecture. Hamilton (1988) used the twodimensional (2D) Ricci flow to give a proof of the uniformization theorem for surfaces of positive genus. This leads to a way for potential applications to computer graphics.
There are many ways to discretize smooth surfaces. The one that is particularly related to a discretization of conformality is the circle packing metric introduced by Thurston (1980). The notion of circle packing has appeared in the work of Koebe (1936). Thurston conjectured (1985) that for a discretization of the Jordan domain in the plane, the sequence of circle packings converges to the Riemann mapping. This was proved by Rodin and Sullivan (1987).
Colin de Verdière Yves (1991) established the first variational principle for circle packing and proved Thurston’s existence of circle packing metrics. This paved a way for a fast algorithmic implementation of finding the circle packing metrics, such as the one by Collins and Stephenson (2003). In 2003, Chow and Luo generalized Yves’ work and introduced the discrete Ricci flow and discrete Ricci energy on surfaces. They proved a general existence and convergence theorem for the discrete Ricci flow and proved that the Ricci energy is convex. The algorithmic implementation of the discrete Ricci flow was carried out by Jin et al. (2008).
Another related discretization method is called circle pattern; it considers both the combinatorics and the geometry of the original mesh and can be looked as a variant to circle packings. Circle pattern was proposed by Bowers and Hurdal (2003) and has been proven to be a minimizer of a convex energy by Bobenko and Springborn (2004). An efficient circle pattern algorithm was developed by Kharevych, Springborn, and Schröder (2006).
Yamabe Flow on Surfaces
The Yamabe problem aims at finding a conformal metric with constant scalar curvature for compact Riemannian manifolds. The first proof (with flaws) was given by Yamabe (1960), which was corrected and extended to a complete proof by several researchers including Trudinger (1968), Aubin (1976), and Schoen (1984). A comprehensive survey on this topic was given by Lee and Parker (1987).
Luo (2004) studied the discrete Yamabe flow on surfaces. He introduced a notion of discrete conformal change of polyhedral metric, which plays a key role in developing the discrete Yamabe flow and the associated variational principle in the field. Based on the discrete conformal class and geometric consideration, Luo gave the discrete Yamabe energy as an integration of a differential 1-form and proved that this energy is a locally convex function. He also deduced from it that the curvature evolution of the Yamabe flow is a heat equation.
In a recent work of Springborn, Schröder, and Pinkall (2008), they were able to identify the Yamabe energy introduced by Luo with the Milnor-Lobachevsky function and the heat equation for the curvature evolution with the cotangent Laplace equation. They constructed an algorithm based on their explicit formula. Another recent work by Gu, Luo, and Yau (2009), which used the original discrete Yamabe energy from Luo (2004), has produced an equally efficient algorithm in finding the discrete conformal metrics.
The rest of the topic is organized as follows. We first introduce some basic concepts and theories of the surface Ricci flow in the smooth setting. Then we present the discrete setting and numerical algorithms to compute the flow. In the final section, we briefly describe the applications for brain mapping, surface matching, and TeichmV’uller shape space. Further details on discrete curvature flows and their variational principles can be found in Luo (2004). The details and source codes of the algorithms presented here can be found in Gu and Yau (2008) and Gu, Luo, and Yau (2009).
Theories on the smooth Surface RICCI Flow
In this section, we introduce the theory of the Ricci flow in the continuous setting, which will be extended to the discrete setting in the section below entitled “Theories on the Discrete Surface Ricci Flow.”
Fundamental Group and Universal Covering Space The closed loops on the surface can be classified by homotopy equivalence. If two closed curves on a surface M can deform to each other without leaving the surface, then they are homotopic to each other. Two closed curves sharing common points can be concatenated to form another loop. This operation defines the multiplication of homotopic classes. All the homotopy classes form the first fundamental group of M. A collection of curves on the surface is a cut graph, if their complement is a topological disk, which is called the fundamental domain of the surface.
For a genus g closed surface, the fundamental group has 2g generators. A set of fundamental group basis {a1,b1,a2,b2, … ,ag,bg} is canonical, if at ,b; have only one geometric intersection, but neither ai,a. nor ai,b. have geometric intersections, where i ^ j. If we slice M along the curves, we can get a disk-like domain with boundary {a1b1a1_1b1_1a2b2a2’1b2’1… agbga-1b-1}, which is called the canonical fundamental domain of the surface M.
A covering space of M is a surface M together with a continuous subjective map p : M ^ M, such that for every q eM there exists an open neighborhood U of q such that p-1(U) (the inverse image of U under p) is a disjoint union of open sets in M, each of which is mapped homeo-morphically onto U by p. If M is simply connected, then M is called the universal covering space of M. Suppose ¢: M ^ M,p = ty°p, then Q is called a deck transformation. A deck transformation maps one fundamental domain to another fundamental domain. All the deck transformations form the deck transformation group, which is isomorphic to the fundamental group. We use the algorithms in Carner et al. (2005) to compute the canonical fundamental group generators.
Riemannian Metric and gaussian Curvature
All the differential geometric concepts and the detailed explanations can be found in Guggenheimer (1977). Suppose S is a C2 smooth surface embedded in R3 with local parameter (u1 ,u2 ). Let r(u1 ,u2 ) be a point on S and dr=r1du1 + r2du2 be the tangent vector r defined at that point, where r1, r2 are the partial derivatives of r with respect to u1 and u2, respectively. The Riemannian metric or the first fundamental form is
The Gauss map G : S ^ S2 from the surface S to the unit sphere S2 maps each point p on the surface to its normal n(p) on the sphere. The Gaussian curvature K(p) is defined as the Jacobian of the Gauss map. Intuitively, it is the ratio between the infinitesimal area of the Gauss image on the Gaussian sphere and the infinitesimal area on the surface.
Let dS be the boundary of the surface S, kg the geodesic curvature, dA the area element, ds the line element, and ^(S) the Euler characteristic number of S. The total curvature is determined by the topology, which satisfies the following Gauss-Bonnet Theorem:
Conformal Deformation
Let S be a surface embedded in M3. S has a Riemannian metric induced from the Euclidean metric of M3, denoted by g. Suppose u : S ^ M is a scalar function defined on S. It can be verified that g = e 2ug is also a Riemannian metric on S. Furthermore, angles measured by g are equal to those measured by g. Therefore, we say g is a conformal deformation from g.
A conformal deformation maps infinitesimal circles to infinitesimal circles and preserves the intersection angles among the infinitesimal circles. In Figure 4.1, we illustrate this property by approximating infinitesimal circles by finite circles. We put a regular circle packing pattern on the texture and map the texture to the surface using a conformal parameterization, where all the circles on the texture still look like circles on the surface, and all the tangency relations among the circles are preserved.
When the Riemannian metric is conformally deformed, curvatures will also be changed accordingly. Suppose g is changed to g = e2u g. Then, the Gaussian curvature will become
where Ag is the Laplacian-Beltrami operator under the original metric g. The geodesic curvature will become
where r is the tangent vector orthogonal to the boundary. According to the Gauss-Bonnet theorem, the total curvature is still 2nx(S), where %(S) is the Euler characteristic number of S.
FIGURE 4.1 Properties of conformal mapping: conformal mappings transform infinitesimal circles to infinitesimal circles and preserve the inter section angles among the circles. Here, infinitesimal circles are approximated by finite ones. Notice that a circle in the texture appears in a scaled one in the texture mapping result. Also notice the angles in the checkerboard pattern preserved in the texture mapping result.
Uniformization Theorem
Given a surface S with a Riemannian metric g, there exist infinitely many metrics conformal to g. The following uniformization theorem states that among all of the conformal metrics, there exists a representative that induces constant curvature. Moreover, the constant will be one of {+1, 0, -1}.
Theorem 4.1 (Uniformization Theorem)
Let (S, g) be a compact two-dimensional surface with a Riemannian metric g, then there is a metric g conformal to g with constant Gaussian curvature everywhere; the constant is one of {+1, 0, -1}. Furthermore, the constant -1 curvature metric is unique.
We call such a metric the uniformization metric of S. According to the Gauss-Bonnet theorem (Equation [4.2]), the sign of the constant Gaussian curvature must match the sign of the Euler number of the surface: +1 for X(S) > 0,0 for x(s) = 0, and -1 for x(S) < 0.
Therefore, we can embed the universal covering space of any closed surface using its uniformization metric onto one of the three canonical surfaces: the sphere S2 for genus zero surfaces with positive Euler number, the plane E2 for genus one surfaces with zero Euler number, and the hyperbolic space H2 for high genus surfaces with negative Euler number (see Figure 4.2). Accordingly, we can say that surfaces with positive Euler number admit spherical geometry; surfaces with zero Euler number admit Euclidean geometry; and surfaces with negative Euler number admit hyperbolic geometry.
Figure 4.2 Uniformization theorem: each surface in M3 admits a uniformization metric, which is conformal to the original metric and induces constant Gaussian curvature; the constant is one of {+1, 0, -1} depending on the Euler characteristic number x of the surface. Its universal covering space with the uniformization metric can be isometri-cally embedded onto one of three canonical spaces: sphere (a), plane (b), or hyperbolic space (c). Here, we show the parameterizations computed by using discrete spherical, Euclidean, and hyperbolic Ricci flows, respectively.
Spherical, Euclidean, and Hyperbolic geometry The unit sphere is with Gaussian curvature +1 and admits the spherical geometry. The rigid motions in spherical geometry are rotations. The geodesics are great arcs. The Euclidean plane is with 0 curvature and admits the Euclidean geometry. Planar translations and rotations form the rigid motion group.
The hyperbolic space model we used in this topic is the Poincaré disk, which is a unit disk on the complex plane, with Riemannian metric
In the Poincaré disk, rigid motion is a Möbius transformation:
the geodesics are circular arcs that are orthogonal to the unit circle; the hyperbolic circle (c, r) (c represents the center, r the radius) coincides with a Euclidean circle (C,R) with
where
We also use the upper half-plane model for hyperbolic space
with the Riemannian metri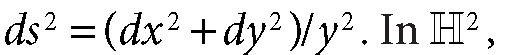
hyperbolic lines are circular arcs and half lines orthogonal to the x-axis. The rigid motion is given by the Möbius transformation:
where z = x + iy is the complex coordinate.
Similarly, the 3D hyperbolic space H3 can be represented using upper half-space model,
with Riemannian metric
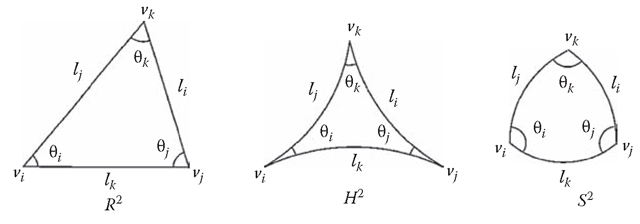
FIGURE 4.3 Euclidean, hyperbolic, and spherical triangles.
In H3, the hyperbolic planes are hemispheres or vertical planes, whose equators are on the xy-plane. The xy-plane represents all the infinity points in H3. The rigid motion in H3 is determined by its restriction on the xy-plane, which is a Möbius transformation on the plane, in the form
Most of the computation is carried out on the xy-plane.
As shown in Figure 4.3, triangles with spherical, Euclidean, or hyperbolic background geometry (meaning triangles in S2, E2, and H2 ) satisfy, different cosine laws:
We can interchange the role of edge and angle and get another three cosine laws:
Based on the cosine laws, curvature flows on smooth surfaces can be generalized to discrete cases.
