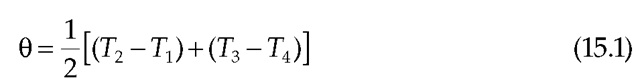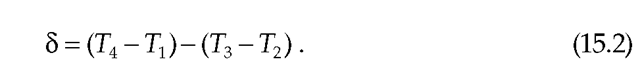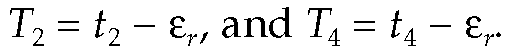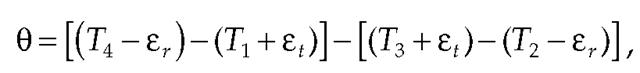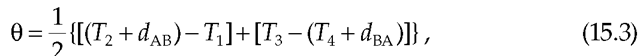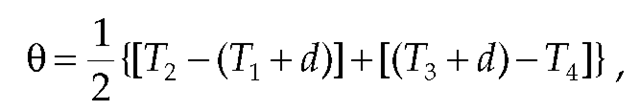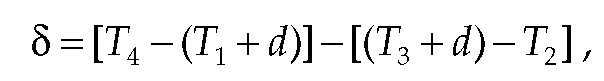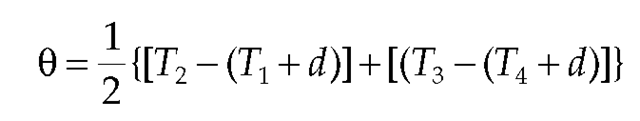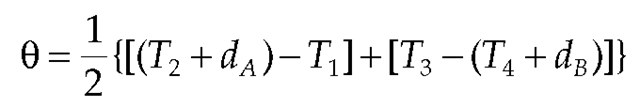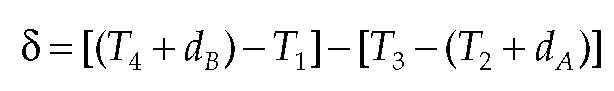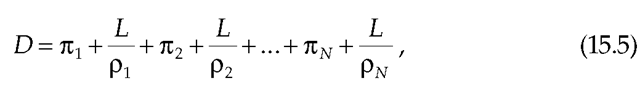As shown elsewhere in this topic, stochastic errors are generally minimized by the NTP mitigation and discipline algorithms. In general, these errors can be further reduced using some kind of timestamping assist in the form of special provisions in the network interface card (NIC) or device driver. Means to exploit these provisions are discussed in this section.
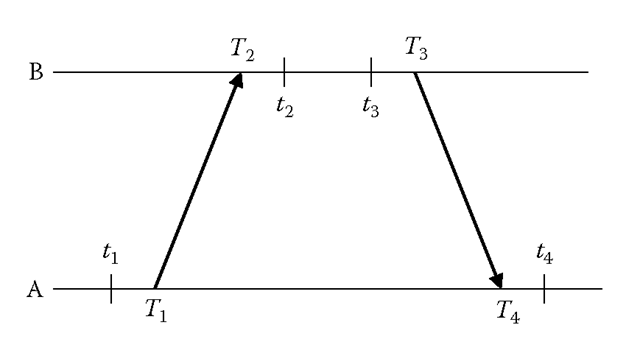
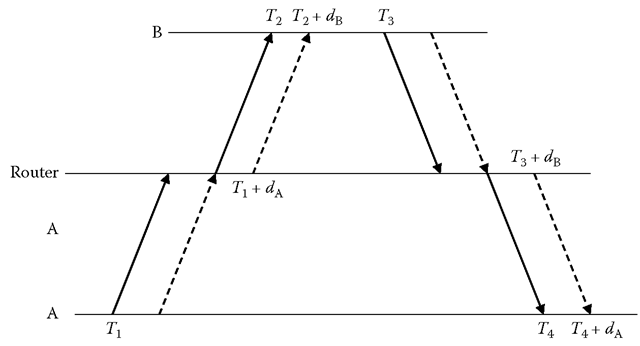
To better understand the issues, consider the common case by which the server and client implement precision clocks that can be read with exquisite accuracy. The object is to measure the time offset of a server B relative to a client A. As shown in Figure 15.2, the NTP on-wire protocol uses the reference timestamps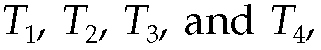
respectively called the origin, receive, transmit, and destination timestamps. In the context of this discussion, reference timestamps are captured just before the first octet of the packet. T1 and T4 are captured by client A from its clock, while T2 and T3 are captured by server B from its clock. The object of the protocol is to determine the time offset 8 of B relative to A and the round-trip delay 5 on the path ABA:
and
Figure 15.2
NTP on-wire protocol/timestamps.
However, the actual timestamps available to the protocol are t1, t2, t3, and t4. The differences between the actual timestamps and reference timestamps are due to queuing and buffering latencies in the operating system, device driver, and NIC. These issues are discussed in this section.
The precision to which the offset and delay can be calculated depends on the precision with which the timestamps can be captured. In general, it is best to capture the timestamps as close to the physical media as possible to avoid various queuing and buffering latencies. There are three general categories of timestamps to consider: those captured in the application software, called softstamps; those captured by the device driver at interrupt time, called drivestamps; and those captured by special hardware from the media, called hardstamps.
The timestamping scheme used in the NTP reference implementation attempts to approximate the reference timestamp as follows: The f, and t3 are softstamps captured by the output packet routine just before the message digest (if used) is calculated and the buffer is passed to the operating system. Applicable latencies include digest overhead, output queuing, operating system scheduling, NIC buffering, and possibly NIC retransmissions.The f2 and f4 are drivestamps captured just after the input packet interrupt routine and before the buffer is queued for the input packet routine. Applicable latencies include NIC buffering, interrupt processing, and operating system scheduling but not input queuing.
If these latencies can be avoided, the remaining latencies are due only to propagation time, packet transmission time, and network queues. Inspection of Equation 15.1 shows that the best accuracy is obtained when the delays on the outbound path T1 ^ T2 and inbound path T3 ^ T4 are statistically equivalent; in this case, we say that the paths are reciprocal. Further refinement demonstrated further in this section shows that, if the reciprocal delays differ by x seconds, the resulting offset error is x/2 s.
There are many workable schemes to implement timestamp capture. Using a different scheme at each end of the link is likely to result in a lack of reciprocity. The following provisions apply:
1. A software timestamp is captured as close to the system input/output (I/O) call as possible.
2. A preamble timestamp is captured as near to the start of the packet as possible. The preferred point follows the start-of-frame (SOF) octet and before the first octet of the data.
3. A trailer timestamp is captured as near to the end of the packet as possible. On transmit, the preferred point follows the last octet of the data and before the frame check sequence (FCS); on receive, the preferred point follows the last octet of the FCS. The reason the capture locations necessarily differ is due to the Ethernet hardware and protocol design. (Note: A sufficiently large and complex field-programmable gate array (FPGA) might be able to deliver the trailer timestamp at the same point as the transmitter, but this does not seem worth the trouble.)
4. In addition to the timestamps, the NIC or driver must provide both the nominal transmission rate and number of octets between the preamble and trailer timestamps. This can be used by the driver or application to transpose between the preamble and trailer timestamps without significant loss of accuracy. The transposition error with acceptable frequency tolerance of 300 PPM for 100-Mb/s Ethernets and a nominal 1,000-bit NTP packet is less than 3 ns.
Except as mentioned in further discussion here, a drivestamp is always a trailer timestamp, and a hardstamp is a preamble timestamp. On transmit, a softstamp is a preamble timestamp; on receive, it is a trailer timestamp. As shown further in this section, the best way to preserve accuracy when single or multiple network segments are involved, some possibly operating at different rates, is the following:
1. The propagation delay measured from the first bit sent in a packet to the first bit received in each direction of transmission must be the same.
2. T1 and T3 must be captured from the preamble timestamp.
3. T2 and T4 must be captured from the trailer timestamp.
Whatever timestamping strategy is deployed, it should allow interworking between schemes so that every combination of strategies used by the server and client results in the highest accuracy possible. As will be shown, this can be achieved only using the above rules.
Timestamp Transposition
With these requirements in mind, it is possible to select either the preamble or the trailer timestamp at either the transmitter or the receiver and to transpose so that both represent the same reference point in the packet. The natural choice is the preamble timestamp as this is considered the reference timestamp in this document and is consistent with IEEE 1588 and likely to be supported by available hardware.
According to the rules given, a transmitter must transpose trailer time-stamps to preamble timestamps, and a receiver must transpose preamble timestamps to trailer timestamps. Transposition must take into account the transmission rate and packet length on the transmit and receive LAN or subnet separately. An NTP packet (about 1,000 bits) is 1 us on a 1,000-Mb/s LAN, 10 us on a 100-Mb/s LAN, and 650 us on a T1 line at 1.544 Mb/s. As will be shown, to drive the residual NTP offsets down to PPS levels, typically within 10 js, the reciprocal delays must match within 10 us. If the reciprocal transmission rates and packet lengths are the same to within 10 js, or one packet time on a 100-Mb/s LAN, the accuracy goal can be met.
In Unix with older NICs, the user-space buffer is copied to a kernel-space buffer chain (mbufs), which then is passed to the driver. The driver waits until the medium becomes idle, then transmits the mbufs using DMA. At completion of the last transfer, the driver captures a drivestamp. However, modern NICs of the PCNET family use a chain of hardware descriptors, one for each buffer, and DMAs directly from user space to an internal 16K first in, first out (FIFO), shared between the transmit and receive sides, and separate frame buffers for each side. The NIC signals an interrupt on completion of the DMA transfer, but one or more frames can be in the FIFO pending transmission, so a more relevant interpretation of the interrupt might be a preamble timestamp.
NTP servers Macabre and Mort are identical Intel Pentium clones running FreeBSD and operating in symmetric modes. They are synchronized to a GPS receiver via a lightly loaded 100-Mb/s LAN and share the same switch. Each server shows nominal offset and jitter of about 25 |js relative to the GPS receiver and a few microseconds relative to each other. Offsets of this order normally would be considered reciprocal. Both machines have been configured to use drivestamps for both transmit and receive, so the transmitters should transpose to preamble timestamps.
However, both machines use NICs of the PCNET family, so what the driver thinks is a trailer timestamp is actually a preamble timestamp. Each peer shows a round-trip delay of about 140 |s with the other. Since 40 |s (four LAN hops) is due to packet transmission time, the remaining 100 |s is shared equally by each server due to buffering in the operating systems and NICs. The measured delay from the transmit softstamp to the transmit drivestamp is about 15 |s, so the transmit NIC delay is about 5 |s. This leaves 35 |s for the receive NIC delay. These measurements were made in a temperature-stabilized, lightly loaded LAN; performance in working LANs will vary.
The example shows the importance that the drivers know the characteristics of the NIC and compensate accordingly. Further improvement in accuracy to the order of the PPS signal requires hardware or driver assist as described later.
Error Analysis
In Figures 15.2 and the following, uppercase variables represent the reference timestamps used in Equations 15.1 and 15.2; lowercase variables represent the actual timestamps captured by the hardware, driver, or software. The on-wire protocol uses the actual timestamps in the same fashion as the reference timestamps but corrected for systematic errors as described in this and following sections. The object is to explore the possible errors that might result from different timestamp strategies.
In the NTP reference implementation, the
transmit softstamps are captured from the system clock just before handing the buffer to the kernel output queue. They are delayed by various latencies represented by the random variable
Thus, we assume
In anticipation of a packet arrival, the NTP reference implementation allocates an input buffer in user space. When a complete packet (chain of mbufs) arrives, the driver copies them to the buffer. The
receive drivestamps are captured from the system clock and copied to a reserved field in the buffer just before handing it to the user input queue. They are delayed by various latencies represented by the random variable
Thus,
As shown in Figure 15.2, the NTP on-wire protocol performs the same calculations as Equations 15.1 and 15.2 but using the actual timestamps. After substitution, we have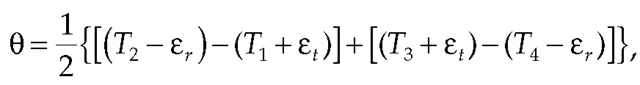
which after simplification is the same as Equation 15.1 on average. On the other hand,
which results in an additional delay of
on average.
While these equations involve random variables, we can make strong statements about the resulting accuracy if we assume that the probability distributions of et and er are substantially the same for both client A and server B. We conclude that, as long as the delays on the reciprocal paths are the same and the packet lengths are the same, the offset is as in Equation 15.1 without dilution of accuracy. There is a small increase in round-trip delay relative to Equation 15.2, but this is not ordinarily a significant problem.
The principal remaining terms in the error budget are nonreciprocal delays due to different data rates and nonuniform transposition between the preamble and trailer timestamps. The errors due to such causes are summarized in following sections.
Reciprocity Errors
The previous analysis assumes that the delays on the outbound and inbound paths are the same; that is, the paths are reciprocal. This is ensured if the propagation delays are the same, the transmission rates are the same, and the packet lengths are the same. In the NTP on-wire protocol, all packets have the same length. If we assume that the transmission rates are the same, the only difference in path delays must be due to nonreciprocal transmission paths. This often occurs if one way is via landline and the other via satellite. It can also occur when the paths traverse tag-switched core networks.
The magnitude of the errors introduced by nonreciprocal delays can be determined with the aid of Figure 15.3, in which we assume that the reference timestamps represent network paths with zero delay, then add outbound delay dAB and inbound delay dBA. The NTP on-wire protocol performs the same calculations as Equations 15.1 and 15.2 using the reference timestamps but ignoring the latencies discussed in the preceding section. After substitution, we have
which after simplification results in an error of
On the other hand,
which results in a round-trip delay of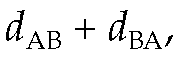
as expected.
Sun Ultra Pogo and Intel Pentium Deacon are synchronized to PPS sources showing typical offset and jitter less than 5 |js. Both are clients of each other via bridged 100-Mb/s LAN segments, so the round-trip delay between the NICs is 40 |s for Sun Ultra Pogo and Intel Pentium Deacon are synchronized to PPS sources showing typical offset and jitter less than 5 |js. Both are clients of each other via bridged 100-Mb/s LAN segments, so the round-trip delay between the NICs is 40 |s for 1,000-bit packets and four hops.
Figure 15.3
Nonreciprocal delay error.
The round-trip delay measured by either machine is about 400 |s, and the jitter is estimated at 25 |s. The measured offset of Pogo relative to Rackety is 89 |s, while the measured offset of Rackety relative to Pogo is -97 |s.
The fact that the two machines are synchronized closely to the PPS signal and the measured offsets are almost equal and with opposite sign suggest that the two paths are nonreciprocal. Of the measured round-trip delay, 40 |s is packet transmission times; the remaining 360 |s must be due to buffering in the operating system and NICs. From the analysis, the offset error is consistent with one path having about 200 |s more overall delay than the other. Of the 360-|s round-trip delay, this suggests Rackety accounts for 80 |s, leaving 280 |s for Pogo.
Transposition Errors
With drivestamps, a trailer timestamp is captured for each packet sent or received. The timestamp is available only at driver interrupt time; that is, at the end of the packet and before the FCS on transmit and after the FCS on receive. However, for NICs with a hardstamping capability, the receive hardstamp is actually a preamble timestamp. Assuming that the timestamps can be passed up the protocol stack as in hardstamping, this requires the preamble timestamp to be transposed to a trailer timestamp.
Without transposing, there could be an error due to the packet transmission time d. However, if this is the case for the reciprocal paths,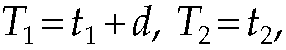
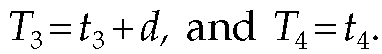In this case, we neglect the time to transmit the FCS, which is 32 ns for 1,000-Mb/s LANs and 320 ns for 100-Mb/s LANs. Then,
which after simplification is the same as Equation 15.1. On the other hand,
which after simplification is the same as Equation 15.2. We conclude that, as long as the transmission rates on the reciprocal paths are the same and the packet lengths are the same, the offset and delay can be computed as in Equations 15.1 and 15.2 without dilution of accuracy.
Interworking Errors
If the outbound and inbound reciprocal paths use the same timestamp-ing strategy, for example, preamble timestamps or trailer timestamps, and have the same transmission rates and packet length, the offset and delay are invariant to the actual packet length and rate. However, if the reciprocal paths use different strategies, errors will result depending on the transmission rate and packet length. Let the delay between the reference and trailer timestamps be d. Then, consider what happens when interworking between various combinations of software, hardware, and driver timestamps without proper transposition. Let A use hardstamps and B drivestamps. Then,
which results in an offset error of -2d, while
results in no error. Many other combinations are possible.
Store-and-Forward Errors
Consider a network with two subnets connected by a router where one subnet operates at 10 Mb/s and the other at 100 Mb/s. Even with hardstamps, store-and-forward errors can occur due to the different packet transmission times. In Figure 15.4, let dA be the packet time for A and dB be the packet time for B. The router sends the packet to B only after the packet has been received from A, assuming the router is not capable of cut-through switching.
If the timestamping strategy is preamble timestamps,
results in an offset error of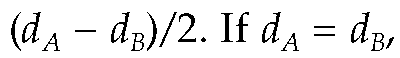
there is no offset error.
Figure 15.4
Two-subnet LAN.
On the other hand,
results in a delay increase of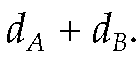
Now, consider the case using preamble transmit timestamps and trailer receive timestamps. In this case, the reciprocal delays are the same, and no offset errors result. This justifies the rules stated at the beginning of Section 15.3. From this, we can conclude that it is not only the timestamping strategies at A and B that must match; some consideration must also be given to the forwarding behavior of the routers in Figure 15.4 that connect A and B when the link speeds differ. Using the preamble timestamp as the transmit timestamp and the trailer timestamp as the receive timestamp solves this problem.
Nonreciprocal Rate Errors
A transmission path can include two or more concatenated network segments that might operate at different rates. The previous analysis assumes that the transmit and receive rates are the same for each network segment, even if different on different segments. The problem considered here is when the transmit and receive rates are different on some segments. This is a common condition on space data links. Assume the total packet transmission time is
where n is the propagation time, L is the packet length in bits, and p is the transmission rate in bits per second. Now, consider the concatenated path delay
where N is the number of segments. If we assume that the outbound and return paths traverse the same segments in reverse order, the total transmission time will be the same in either direction. If the timestamps are taken as described, the delays are reciprocal, and accuracy is not diluted.
Equation 15.5 can be written
where the R in the second term on the right represents the overall transmission rate, which in the example is considered the same in both directions. Now, consider where the overall transmission rates are not the same in both directions. Let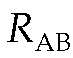
be the overall outbound transmission rate, let
be the overall inbound transmission rate, and compute
as in Equation 15.6. The apparent offset and delay can be obtained from Equations 15.3 and 15.4, which yields the offset error
Subtracting this value from the apparent offset yields the correct offset.
One of the most useful applications of Equation 15.7 is with the Proximity-1 space data link protocol used with Mars orbiters and landers. Compared to typical LANs on Earth, space data links operate at low rates, so the delays can be significant. Typically, the uplink from a surface vehicle to an orbiter carries instrument data at a relatively high rate, while the downlink carries telemetry and ACKs (acknowledgments) at a relatively low rate, so rate correction is important. Since the downlink and uplink rates are selected by mission control and known by the spacecraft computer, Equation 15.7 can be used to correct the apparent offset.
