Basic Geometric Modeling Tools (Basic Computer Graphics) Part 3

Distance Formulas

The next two sections describe a number of formulas that are handy for applications.

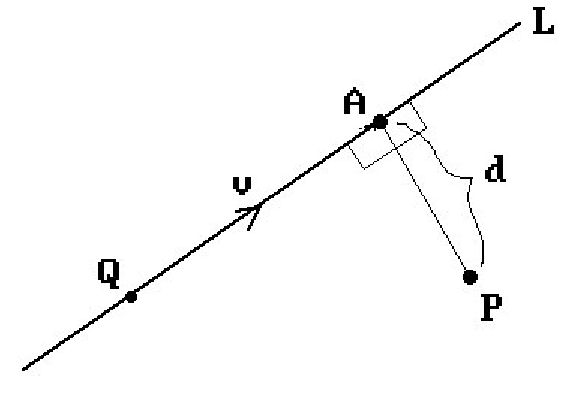
Formula. Let L be a line defined by a point Q and direction vector v and let P be a point. The point

Figure 6.14. Computing the distance from a point to a line.

is the unique point of L that is closest to P. If d is the distance from P to L, then

Alternatively,

Proof. We shall only prove the first formula. The second is Exercise 6.6.1. Consider Figure 6.14. We seek the point A so that AP is orthogonal to v (Theorem 4.5.12 in [AgoM05]). The vector

is the orthogonal projection of

is orthogonal to v. ThenA solution that is concerned with minimizing the number of arithmetic operations needed to solve the problem can be found in [Morr91].

A straightforward generalization of Formula 6.6.1 is 6.6.2 Formula. The distance d from a point P to a plane X which contains a point Q and has orthonormal basisis    given    by

Furthermore,

is the unique point of X which is closest to P.

 

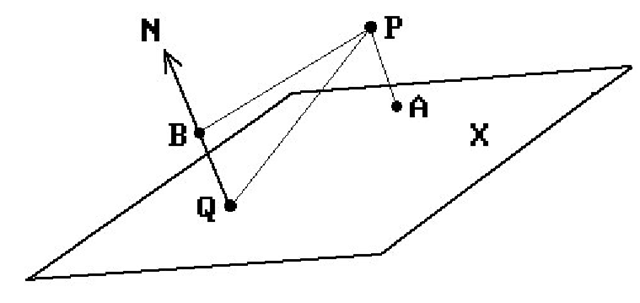
Figure 6.15. Computing the distance from a point to a plane.

If one has a normal vector to a plane, then the formula for the distance of a point to it is much simpler.

Formula. The distance d from a point P to a plane X that contains the point Q and has normal vector N is given by

The point

is the unique point of X that is closest to P. Proof. See Figure 6.15. The vector

is the orthogonal projection of QP onto N. Therefore, d = |w|. Define

Thenis    the    unique    point    of X that is closest to P because AP is orthogonal to the plane (Theorem 4.5.12 in [AgoM05]).

Formula 6.6.3 can be restated in terms of coordinates as follows:

Formula. If X is a hyperplane in Rn defined by equation

then the distance from X to the origin is

Proof. Note thatis    a    normal    vector    to    plane    X. Therefore, the formula is basically equation (6.22) written in coordinate form. For an efficient formula that avoids square roots see [Geor92].

Two special cases of Formula 6.6.4 are worth noting. The distance from the origin to the line in the plane with equationis

The distance from the origin to the plane in R3 with equationis

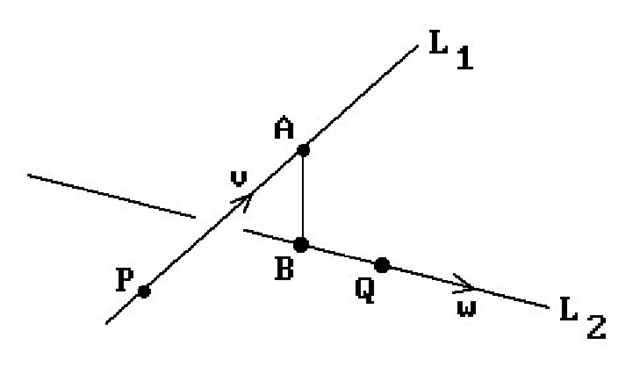
Formula. Let L1 be the line defined by a point P and direction vector v. Let L2 be the line defined by a point Q and direction vector w. Assume that the lines are not parallel. The distance d between L1 and L2 is given by

where

Furthermore, the pointis    the unique point of L1 which is closest to

L2. Similarly, the point_    is    the unique point of L2 which is closest to L1. If the lines intersect, then A = B and we have formulas for the intersection point.

Proof. See Figure 6.16. Let A = P + sv and B = Q + tw be typical points on L1 and L2, respectively. Clearly, d = d(s,t) = dist(A,B), where the vector AB = PQ – sv + tw is orthogonal to both v and w (Theorem 4.5.12 in [AgoM04]).

Figure 6.16. Computing the distance between two lines.

Expanding the two conditions AB · v = 0 and AB · w = 0 reduces to the equations

with the indicated solutions. By the Cauchy-Schwarz inequality, the denominator D is zero precisely when the vectors v and w are parallel.

Area and Volume Formulas

This section contains some more useful formulas. The “proofs” of these formulas will rely on simple-minded geometric observations and will not be very rigorous. For rigorous proofs one would need to use a theory of areas and volumes. The most elegant approach would be via differential forms. See [Spiv65] or Section 4.9 in [AgoM05]. Finally, the formulas below are “mathematical” formulas. For efficient ways to compute them see [VanG95].

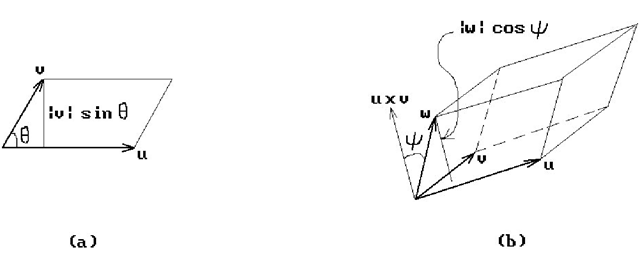
Formula. The area A of a parallelogram defined by two vectors u and v in R2 is given by

Proof. The first equality follows from properties of the cross product and the fact that A is the product of the height of the parallelogram and the length of its base. See Figure 6.17(a). The second follows from direct computation of the cross product and the indicated determinant.

Formula. The volume V of a parallelopiped defined by vectors u, v, and w in R3 is given by

Figure 6.17. The area of a parallelogram and volume of a parallelopiped.

Proof. By a rigid motion we can arrange it so that u and v lie in the plane R2. The first equality follows from the fact that V is the product of the height of the parallelopiped and the area of its base. See Figure 6.17(b). The second equality is a property of the triple product.

Note that Formula 6.7.1 is a special case of Formula 6.7.2 where we let

Formula. The area A of a triangle defined by two vectors u and v in R2 is given by

Proof. This is an immediate corollary of Formula 6.7.1. Of course, we could also use the well-known formula

(The height is just the length of the orthogonal complement of v with respect to u.)

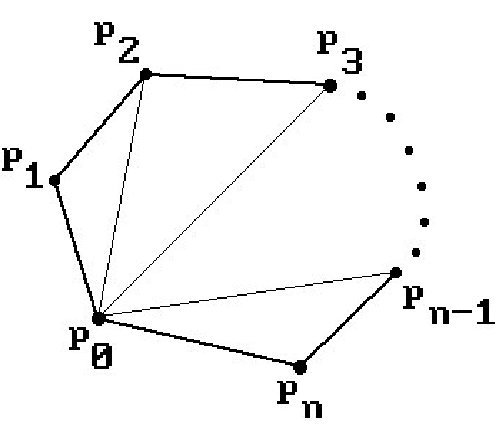
Formula. The area A of a polygon defined by points in

R2 is given by

Figure 6.18. Computing the area of a polygon.

Proof. Consider Figure 6.18 and use Formula 6.7.3. The argument also works for nonconvex polygons.

Formula. The signed volume V of a tetrahedron with verticesand p4 is given by

whereThe value for  V will be positive if we order the points so that  the ordered basisinduces    the    standard orientation of R3.

Proof. The first equality follows from Formula 6.7.2 and the fact that the paral-lelolopiped defined bycan    be    decomposed    into    six    tetrahedra of equal volumes. The second equality in formula (6.31) follows from basic properties of the determinant, in particular, the fact that the determinant of a matrix is unchanged if a row of the matrix is subtracted from another row.

Definition. Letbe a differentiable curve in the plane. LetThe set is called the region subtended by the curve γ from the point p. See Figure 6.19(a).

Formula. Letbe    a curve in the plane. The signed area A of the region subtended by the curve γ from the origin is given by

Figure 6.19. Area subtended by curve from origin.

Proof. See Figure 6.19. Let=    b  be  a partition  of  [a,b]. Letbe    the signed area of the triangleSince

for some

we get that

by Formula 6.7.3. The sign ofwill be positive if the curve is moving in a counterclockwise direction about the origin atand negative otherwise. Adding up all theis clearly an approximation to A and a Riemann sum that converges to the integral in the formula as the norm of the partition goes to zero.