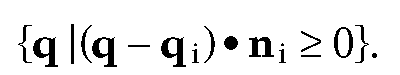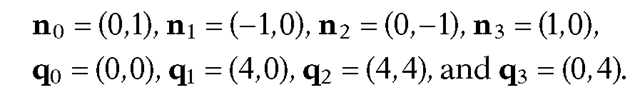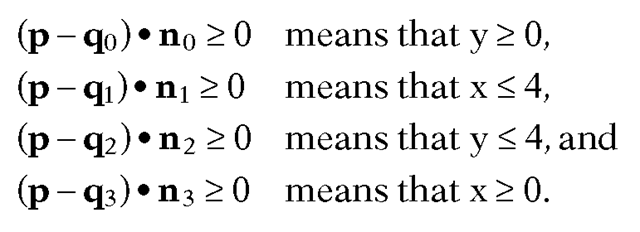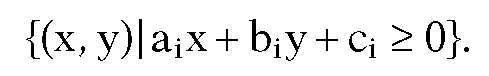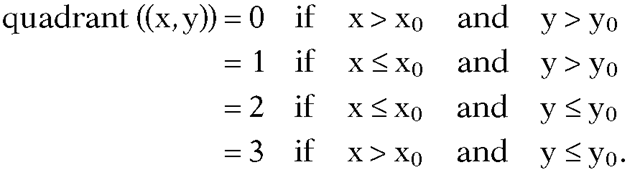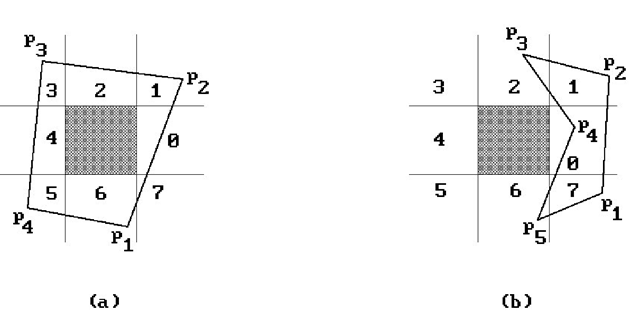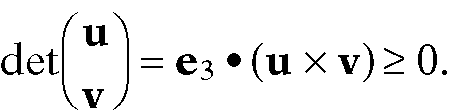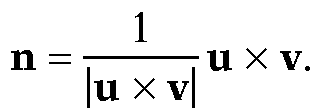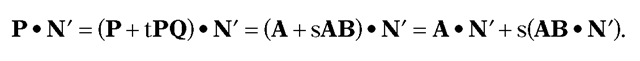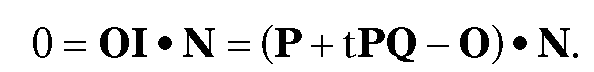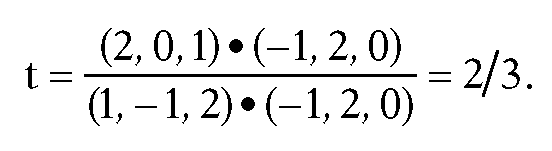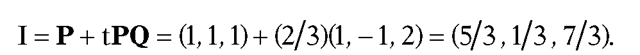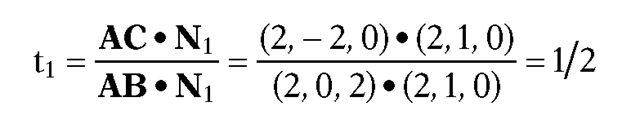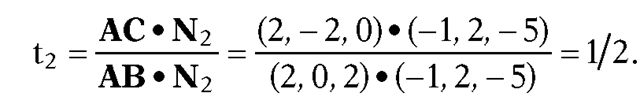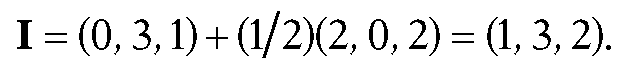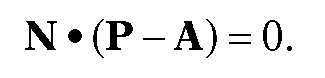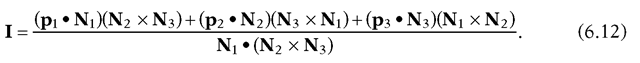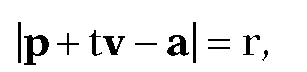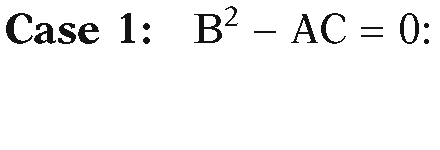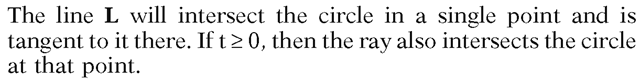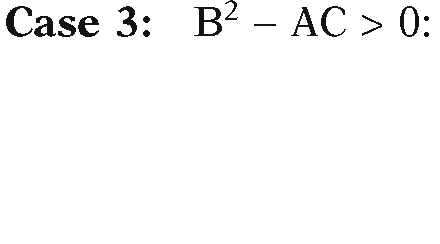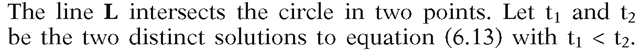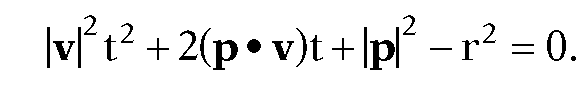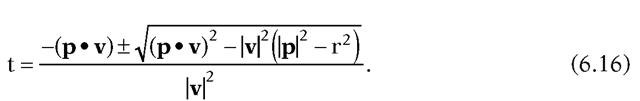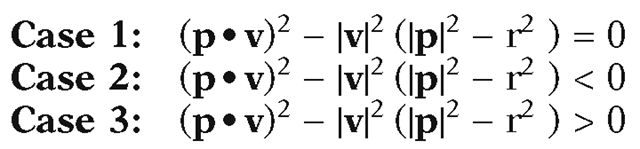Surrounding Tests
Along with finding intersections, determining whether or not a point belongs to a two-or three-dimensional region is another common task. This section looks at some simple tests to answer the question
“Does the point p belong to the linear polyhedron Q?”
We call them “surrounding” tests because the question could also be thought of as one that asks whether a point is inside a closed curve or surface (the boundary of the polyhedron Q in this case). Surrounding tests fall naturally into two classes—those that deal with convex polyhedra and those that handle arbitrary polyhedra. Our discussion will also separate these two cases, but the reader should note the following: In either of these two cases it is usually a good idea to use a bounding box B for Q and first check whether p belongs to B or not. The reason is that it is very easy to check if a point belongs to a box. If p does not belong to B, then it will not belong to Q and there would be no need to do a lot of work to test p against Q.
We begin with tests for a convex polyhedron Q.
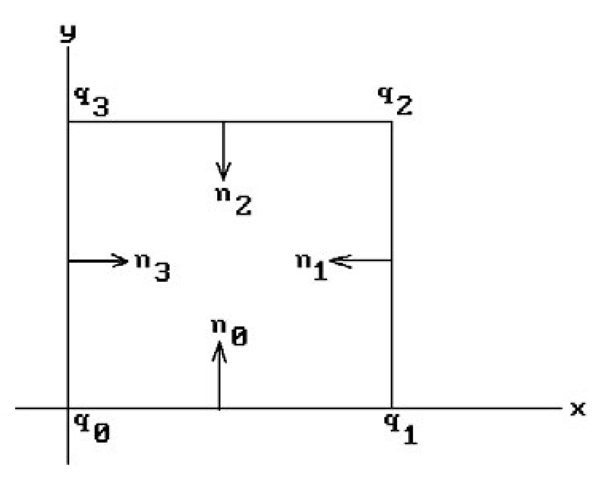
The Normals Test (Convex Q). A convex polyhedron Q is the intersection of a collection of halfplanes associated to the faces of Q. Suppose that we are given a normal vector ni and vertex qi for the ith face, so that the ith halfplane can be expressed in the form
The point p will belong to Q if and only if
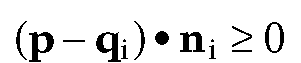for all i. As a trivial example, suppose that Q is the unit square
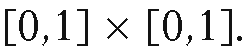It has four faces. Let
See Figure 6.5. If
then 
Figure 6.5. Surrounding test based on normals.
These constraints on x and y are clearly the correct ones.
The Equations Test (Convex Q). This test is really just a rewriting of the previous test. We shall describe it in the two-dimensional case. Let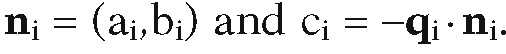
With this notation, the ith halfplane above is just the set
It follows that p = (x,y) will belong to the polygon if and only if
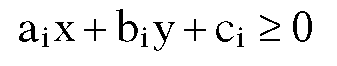for all i. What is the difference between the normals and equations test? Not much. Deciding which test to use basically depends on how data has been stored in a program. Did one store vectors ni or coefficients ai, bi, and ci?
The normals and equations tests can be generalized to a test for whether or not a convex polyhedron P is contained in Q. One simply checks if all the vertices of P belong to Q. If they do, then P will be contained in Q, otherwise not.
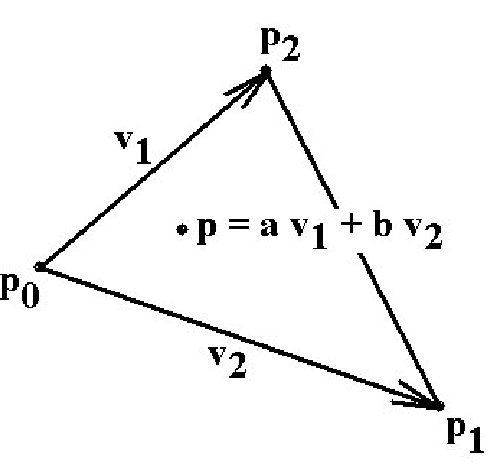
The Barycentric Coordinate Test (Convex Q). This test ([Bado90]) applies only to polyghedron in the plane. We think of
as a fan of triangles
and then check each triangle to see whether p belongs to it by computing its barycen-tric coordinates with respect to the vertices. For example, in the case of the triangle 
express p0p in the form
The point p will belong to
if and only if
See Figure 6.6. If one keeps track of the number of triangles that cover the point, then one can extend the test to nonconvex polygons.
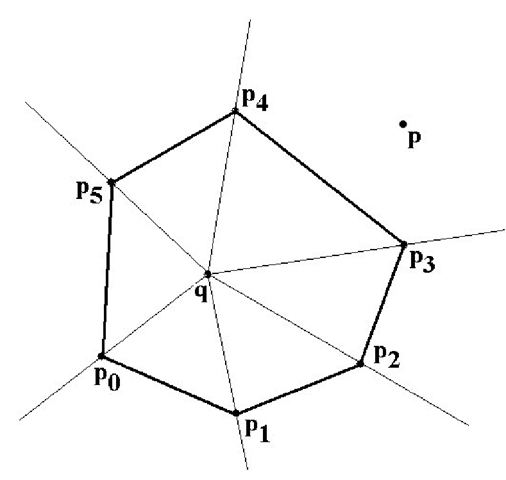
The Wedge Test (Convex Q). This test ([PreS85]) also applies only to polygons in the plane. One adds a central point q to the polygon
say the centroid.
Figure 6.6. Surrounding test based on barycentric coordinates.
Figure 6.7. Surrounding test based on wedges.
The rays from this point through all the vertices of Q then divide the plane into infinite wedges that are cut in half by the associated edge of Q. One can find the wedge that contains p by doing a binary search for the angle of qp among the angles of the vectors qpi. Finally one checks where p lies with respect to the edge of Q in the wedge. See Figure 6.7. Because binary search is fast, this can be a good algorithm.
Next, we look at surrounding tests for arbitrary (possibly nonconvex) polyhedra.
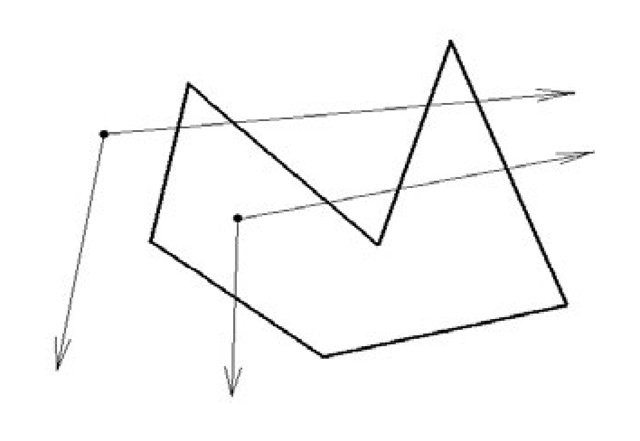
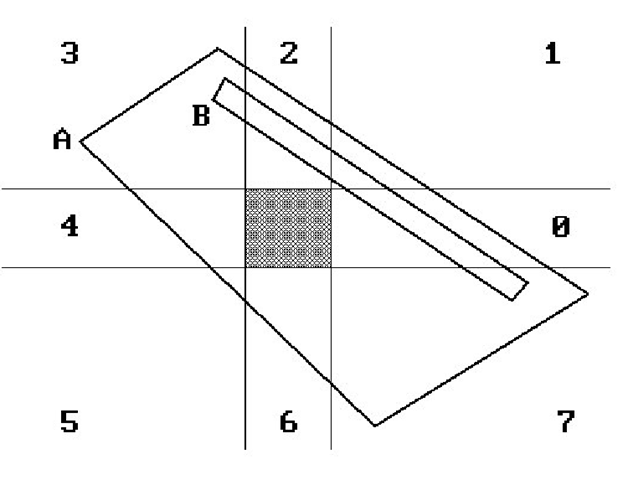
The Parity or Crossings Test (Arbitrary Q). For this test one checks how many times any ray starting at p will intersect the boundary of Q. If it intersects an even number of times, p is outside Q. If it intersects an odd number of times, p is inside Q. See Figure 6.8. For this to work though one must count an intersection twice if the ray is “tangent” to the boundary of Q at that point. In the two-dimensional case “tangent” means that the boundary edges containing the intersection point lie entirely to one side of the ray. In the three-dimensional case the boundary faces containing the point should lie entirely to one side of a “tangent” plane containing the ray. The polyhedron does not have to be convex for the parity test, but it can be made more efficient in the convex case.
The intersection tests and tests for tangency could make this a somewhat complicated test to implement without some tricks, especially in three dimensions. We indicate a few details in the planar case.
Figure 6.8. Surrounding test based on parity.
In this case the ray from p is usually chosen to be parallel to the x-axis with direction vector (0,1). To avoid the problem case where a vertex of Q actually lies on the ray, one pretends that all such points lie slightly above the ray. Next, one can easily tell if the ray intersects an edge. If the y-coordinates of the endpoints have the same signs, then the ray does not intersect. If they have opposite signs, then there will be an intersection if both x-coordinates are to the right of the x-coordinate of p. If the x-coordinates straddle the point, then one must compute the intersection and check on which side of p it lies.
The Angle Counting Test. This test, which applies only to planar polygons Q, is based on the topological concept of winding number that counts how many times one object “winds around” another. See Section 9.3 in [AgoM05]. The test, due to Weiler ([Weil94]), was motivated by the solution to a slightly different problem, which we shall describe first.
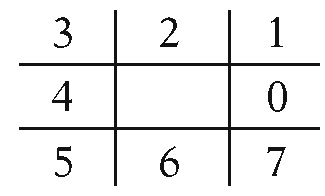
Let W be a rectangular “window” in the plane. Assume that Q also lies in the plane and that the boundaries of W and Q are disjoint. The question we want to answer is whether the two spaces are disjoint. Just because their boundaries are disjoint does not mean that the spaces are since one could contain the other. We present an algorithm ([Roge98]) that involves counting certain angles. In the topological case we would have to sum up infinitesimal angles, but here we do not have to be that accurate. Let us number the “octants” around W as shown below:
For a point p, let c(p) denote the number of the octant into which it falls. For each oriented polygon edge e, define the recursive angle increment function d0(e) by
One can prove the following:
6.3.1 Theorem. The polygon Q will be disjoint from the window W if
is 0 and surround the window if
Figure 6.9 shows some examples. Figure 6.10 shows the need for the adjustment to
in the
case.
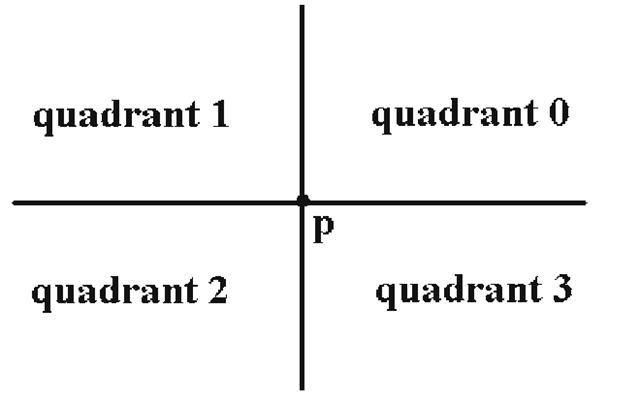
We now return to our original problem about when a point p belongs to a polygon Q, Weiler’s angle counting algorithm. Weiler basically takes the algorithm described above, shrinks the window W to a point p, and adjusts the algorithm accordingly. Now we classify the vertices of Q with respect to the quadrant into which they fall with respect to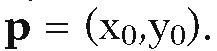
See Figure 6.11. The quadrants are encoded via integers 0, 1, 2, or 3. Given a point (x,y), define
Figure 6.9. Window surrounding test based on angle counting.
Figure 6.10. Example showing need for care in angle counting.
Figure 6.11. Surrounding test based on angle counting.
With our choice of inequalities, the point p falls into quadrant 2 and the other points on the vertical or horizontal axis in Figure 6.11 are encoded by the number of the quadrant to the left or below it, respectively. The actual program that computes the total angle Ω that is traced out by Q about p is quite simple. We start with a value of 0 and then add to Ω the difference d0 in quadrant values from one vertex to the next. The only problem is that we will again have to worry about moves between diagonal quadrants (too large of an angle). Therefore, increments will have to be adjusted using the function adjustDelta below. To compute the adjustment, one also needs a function that determines when a polygon edge passes to the left or right of p at y-level y0. Here are the functions we need:
The reader can find a C program for computing Ω in [Weil94]. The main result is then the following:
6.3.2Theorem. If p does not lie on the boundary of Q, then it is outside polygon Q if
is 0 and inside if
If p lies on the boundary, then the algorithm will return
depending on whether the interior of Q was to the left or right of p with respect to the orientation of
Weiler’s angle counting algorithm extends to polygons Q with holes if one knows which is the outside boundary. The point p must be inside the outside boundary and outside the hole boundaries. There is also an extension to nonsimple polygons, such as polygons that intersect themselves.
Finally, we would to point the reader to the paper by Haines ([Hain94]) that analyzes a variety of “point-in-planar-polygon” tests with some detailed conclusions about which algorithm to use in which situation. Both the time and the amount of extra storage that is needed must be taken into account. Choosing efficient implementations of the algorithms is obviously also important. Haines has code for a parity algorithm, two versions of algorithms using normals, and an algorithm based on grids. A reader who is looking for the most efficient algorithm really needs to read Haines’ paper, but a rough summary of his recommendations is the following:
Orientation-Related Facts
When is a polygon P convex? The answer to this question is clear if P is defined as the intersection of halfplanes, but the more typical way that polygons are presented is via their boundary, that is, by a sequence of points. Therefore, the “real” question is “When does a sequence of points (in a plane) define a convex polygon?” One test is based on whether segments keep “turning” in one direction.
Definition. Two linearly independent vectors u and v in R2 are said to determine a left turn if the ordered basis (u,v) determines the standard orientation. Otherwise, we say that they determine a right turn. If the vectors are linearly dependent, then we will say that they determine both a left and right turn.
The notion of left or right turning vectors leads to the following intuitively obvious convexity test:
6.4.1 Theorem. (Convexity test for polygons) Assume that a planar polygon P is defined by a sequence of points
The polygon P will be convex if and only if the vectors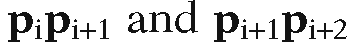
either all determine left turns or all right turns.
Another way to express this test is to say that as one traverses the boundary of the polygon, successive edges either all make left or right turns. Alternatively, vertices of the polygon always lie on the same side of the previous edge as the one before.
There is a simple test for when two vectors u and v determine a left turn: It happens if and only if
Therefore, the convexity test above is easy to program.
Next, suppose that the polygon F is the face of a solid S in R3 and that p is a point in the interior of F.
Definition. Let n be any normal for F. We say that n is an inward-pointing normal to F with respect to the solid S, if the segment
is entirely contained in the solid for some
In that case,
is called an outward-pointing normal for F with respect to S.
There is an easy way to determine if a normal is inward- or outward-pointing for a convex solid S. If q is any point in the interior of S, then n will be an outward-pointing normal for F if otherwise it is inward-pointing.
Definition. If P is a polygon in a plane X, an orientation of P is an orientation of X. An oriented polygon is a pair (P,o), where P is a polygon and o is an orientation of P.
A choice of a normal vector n to a face F of a solid defines an orientation of the face. Choose an ordered basis (u,v) for the plane X generated by the face so that (u,v,n) induces the standard orientation of R3. The orientation of X induced by (u,v) is well-defined.
Definition. The orientation [u,v] of X is called the orientation of F induced by n.
Conversely, an orientation o = [u,v] of the face determines the well-defined unit normal vector
Definition. The vector n is called the normal vector of F induced by the orientation o.
Figure 6.12. Finding the intersection of two segments.
Faces are usually defined by listing their vertices in some order. This ordering defines an orientation and normal vector in a unique way. These are called the induced orientation and induced normal vector, respectively. For example, if the face is defined by
then the induced normal vector is
(assuming that
and p2 are noncollinear). Conversely, an orientation or normal vector for a face defines a unique ordering of its vertices called the induced ordering.
All this extends to the case of an (n – 1)-dimensional face F of an n-dimensional solid S in Rn, in particular, to the case n = 2 and edges of polygons in the plane.
Finally, if one has a set of either all outward- or all inward-pointing normals for a polygon, then another way to test for its convexity is to take successive cross products of the edges and their normals and see if the vectors we get all point the same way.
Simple Intersection Algorithms
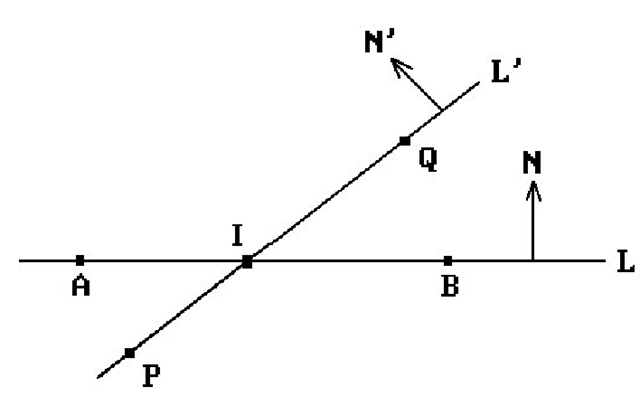
6.5.1 Problem. Find the point I that is the intersection of two planar segments [A,B] and [P,Q].
Solution. Let L and L’ be the lines determined by A,B and P,Q, respectively. See Figure 6.12. Since I, if it exists, must belong to both L and L’, we can express I in the form 
for some s and t. Assume that N and N’ are two vectors which are perpendicular to L and L’, respectively. It follows that
or
Similarly,
or
Of course, s and t may not be defined if the denominators in (6.6) and (6.7) are zero, but this happens precisely when L and L’ are parallel.
This leads to the following solution to Problem 6.5.1:
In this case, use equations (6.6) and (6.7) to compute s and t. If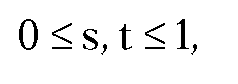 
then the segments [A,B] and [P,Q] intersect in the point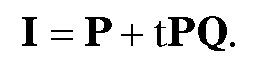 
Case 2. [A,B] and [P,Q] are parallel.
There are two steps in this case.
(1) Check to see if L and L’ are the same line. This can be done by simply checking if they have a point in common. For example, if AP · N = 0, then they do and L = L’. If L is not the same line as L’, then the segments will not intersect.
(2) If L = L’, then we still need to check if the segments intersect. One can reduce this to a problem of segments in R, because the problem is equivalent to asking if the segments [0,|AB|] and [|AP|,|AQ|] intersect.
Unfortunately, although the two steps in Case 2 are a straightforward solution to the mathematical problem, implementing this in a way that produces correct results on a computer is not easy because of round-off errors.
One other issue must still be addressed before we leave the solution to Problem 6.5.1. How does one get the normal vectors N and N’. Since we are in the plane, this is easy. If V = (a,b) is a vector, then (-b,a) is a vector perpendicular to V. Finally, for a solution that is concerned with minimizing the number of arithmetic operations needed to solve the problem see [Pras91].
6.5.2 Problem. Find the intersection I of a line L and a plane X in R3. Assume that L is defined by two distinct points P and Q and that X contains a point O and has normal vector N.
Solution. Since I lies on L we can again express I in the form
for some t. Furthermore, OI must be orthogonal to N. Therefore,
Solving for t leads to
Of course, t is only defined if PQ and N are not orthogonal, that is, L is not parallel to X. The parallel case is again a tricky case for a computer program. One needs to determine whether or not L lies in X.
Example. Find the intersection I of the line L containing points P(1,1,1) and Q(2,0,3) with the plane X which has normal vector N = (-1,2,0) and contains O(3,1,2).
Solution. Substituting into (6.9) gives
Therefore
Problem 6.5.2 easily generalizes to the case where X is a hyperplane in
It also generalizes to 6.5.4 Problem. Find the intersection of a line L with a k-dimensional plane X in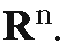 
Assume that
are orthogonal normal vectors for X. Assume
also as before that P and Q are points on L and O is a point on X.
Solution. Define numbers ti by
The ti will be defined provided that L is not parallel to X, which is a special case that must be treated separately. If
then L intersects the plane X in the
point
6.5.5 Example. Find the intersection I of the lines L and L’ in R3, where L contains the points A(0,3,1) and B(2,3,3) and L’ contains the points C(2,1,1) and D(0,5,3).
Solution. A direction vector for
Two orthogonal vectors normal
to
Then
and
Since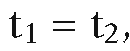
the intersection I exists and
The reader may wonder where N1 and N2 came from. One can either assume that they were given or find two such vectors as follows: Take any two vectors orthogonal to CD and then apply the Gram-Schmidt orthogonalization algorithm to these. An alternate solution to this problem is to observe that L and L’ intersect if and only if they lie in a plane X. A normal to this plane is N = AB x CD. Therefore the lines intersect if C and D satisfy the plane equation
To actually find the intersection, find a normal N1 to L in X (using, for example, the Gram-Schmidt algorithm on N, AB, CD). Now the problem is to find the intersection of a line L’ with the hyperplane L in X with normal N1. The formula from Problem 6.5.2 applies to this variation of the intersection problem also.
We should point out that Formula 6.6.5 in Section 6.6 provides a more direct formula for the intersection of two lines in R3.
6.5.6 Problem. To find the intersection I of three planes
, which are
defined by points pi and normal vectors Ni. We assume that the vectors Ni are linearly independent, that is, the planes are pairwise nonparallel.
Solution. One needs a simultaneous solution to the equations 1,2,3. The solution is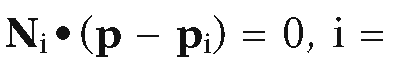
Figure 6.13. Finding the intersection of a ray and a circle.
Equation (6.12) is just a fancy way of writing the solution to this systemof three equations. It is easy to check that I satisfies the equations. Note that
is just the determinant of that system.
The next two problems find the intersection of a ray with a circle. We shall use the following notation: X will denote a ray from a point p in a direction v and L will denote the line through p with direction vector v. 6.5.7 Problem. To find the intersection q, if any, of the ray X and the circle Y with center a and radius r.
Solution. See Figure 6.13. Now, q can be written in the form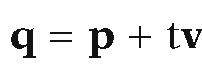
and so we need to solve for t satisfying
or equivalently,
Let
Equation (6.13) can be rewritten in the form
By the quadratic formula, the roots of (6.14) are
Note that A cannot be zero because
That leaves three cases:
Both the line L and the ray miss the circle.
A special case of Problem 6.5.7 is 6.5.8 Problem. To find the intersection q, if any, of the ray X and the circle Y with radius r centered at the origin.
Solution. In this case we need to solve for t satisfying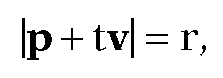 
or equivalently,
It follows that
The three cases in Problem 6.5.7 reduce to
with the same answers as before.
