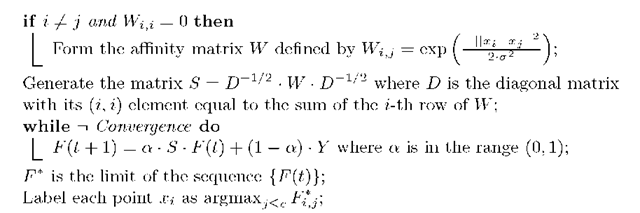Abstract
Malware is any computer software potentially harmful to both computers and networks. The amount of malware is growing every year and poses a serious global security threat. Signature-based detection is the most extended method in commercial antivirus software, however, it consistently fails to detect new malware. Supervised machine learning has been adopted to solve this issue, but the usefulness of supervised learning is far to be complete because it requires a high amount of malicious executables and benign software to be identified and labelled previously. In this paper, we propose a new method of malware detection that adopts a well-known semi-supervised learning approach to detect unknown malware. This method is based on examining the frequencies of the appearance of opcode sequences to build a semi-supervised machine-learning classifier using a set of labelled (either malware or legitimate software) and unlabelled instances. We performed an empirical validation demonstrating that the labelling efforts are lower than when supervised learning is used while the system maintains high accuracy rate.
Keywords: malware detection learning, machine learning, semi-supervised learning.
Introduction
Malware is defined as any computer software explicitly designed to damage computers or networks. While in the past malware writers seek ‘fame and glory’, currently their motivation has evolved to malicious economic considerations [1].
The commercial anti-malware software is highly dependant on a signature database [2]. A signature is a unique sequence of bytes that is always present within malicious executables and in the files already infected. The main issue of this approach is that malware analysts must wait until new malware has harmed several computers to generate a signature file and provide a solution. Analysed suspect files are compared with this list of signatures. When the signatures match, the file being tested is classified as malware. Although this approach has been proven as effective when threats are known in beforehand, these signature methods are surpassed with large amounts of new malware.
Machine-learning-based approaches train classification algorithms that detect new malware, by means of datasets composed of several characteristic features of both malicious and benign software. Schultz et al. [3] were the first to introduce the concept of applying machine-learning models to the detection of malware based on their respective binary codes. Specifically, they applied several classifiers to three different feature sets: (i) program headers, (ii) strings and (iii) byte sequences.
Later, Kolter et al. [4] improved Schulz’s results by applying n-grams (i.e., overlapping byte sequences) instead of non-overlapping sequences. This approach employed several algorithms, achieving the best results with a boosted decision tree. Likewise, substantial research has focused on n-gram distributions of byte sequences and data-mining [5,6].
Additionally, opcode sequences have recently been introduced as an alternative to byte n-grams [7]. This approach appears to be theoretically better than byte n-grams because it relies on source code rather than the bytes of a binary file that can be easier changed than code [8].
However, these supervised machine-learning classifiers require a high number of labelled executables for each of the classes. Sometimes, we can omit one class for labelling, such as in anomaly detection for intrusion detection [9]. It is quite difficult to obtain this amount of labelled data for a real-world problem such as malicious code analysis. To gather these data, a time-consuming process of analysis is mandatory, and in the process, some malicious executables are able to surpass detection.
Semi-supervised learning is a type of machine-learning technique specially useful when a fixed amount of labelled data exists for each file class. These techniques generate a supervised classifier based on labelled data and predict the label for every unlabelled instance. The instances whose classes have been predicted surpassing a certain threshold of confidence are added to the labelled dataset. The process is repeated until certain conditions are satisfied (a commonly used criterion is the maximum likelihood found by the expectation-maximisation technique). These approaches enhance the accuracy of fully unsu-pervised methods (i.e., no labels within the dataset) [10].
Given this background, we propose here an approach that employs a semi-supervised learning technique for the detection of unknown malware. In particular, we utilise the method Learning with Local and Global Consistency (LLGC) [11] able to learn from both labelled and unlabelled data and capable of providing a smooth solution with respect to the intrinsic structure displayed by both labelled and unlabelled instances. For the representation of executables, we propose the adoption of LLGC for the detection of unknown malware based on opcode sequences [7]. However, the presented semi-supervised methodology is scalable to any representation susceptible to be represented as a feature vector.
Summarising, our main findings in this paper are: (i) we describe how to adopt LLGC for opcode-sequence-based unknown malware detection, (ii) we empirically determine the optimal number of labelled instances and we evaluated how this parameter affects the final accuracy of the models and (iii) we demonstrate that labelling efforts can be reduced in the malware detection industry, while still maintaining a high rate of accuracy in the task.
Opcode-Sequence Features for Malware Detection
To represent executables using opcodes, we extract the opcode-sequences and their frequency of appearance. Specifically, we define a program p as a set of ordered opcodes o, p = (01, o2, o3, o4,…, oe-1, oe), where I is the number of instructions I of the program p. An opcode sequence os is defined as a subset of opcodes within the executable file where
it is made up of opcodes o,os = (o1,o2,o3,…, omi,om) where m is the length of the sequence of opcodes os. Consider an example code formed by the opcodes mov, add, push and add; the following sequences of length 2 can be generated: s1 = (mov,add), s2 = (add, push) and S3 = (push, add).
Afterwards, we compute the frequency of occurrence of each opcode sequence within the file by using term frequency(tf) [12] that is a weight widely used in information retrieval:
where riij is the number of times the sequence si,j (in our case opcode sequence) appears in an executable e, and 
is the total number of terms in the executable e (in our case the total number of possible opcode sequences).
We define the Weighted Term Frequency (WTF) as the result of weighting the relevance of each opcode when calculating the term frequency. To calculate the relevance of each individual opcode, we collected malware from the Vx-Heavens website1 to assemble a malware dataset of 13,189 malware executables and we collected 13,000 executables from our computers. Using this dataset, we disassemble each executable and compute the mutual information gain for each opcode and the class:
where
X is the opcode frequency and Y is the class of the file (i.e., malware or benign software), p(x,y) is the joint probability distribution function of X and Y, and p(x) and p(y) are the marginal probability distribution functions of X and Y. In our particular case, we defined the two variables as the single opcode and whether or not the instance was malware. Note that this weight only measures the relevance of a single opcode and not the relevance of an opcode sequence.
Using these weights, we computed the WTF as the product of sequence frequencies and the previously calculated weight of every opcode in the sequence:
where weight(oz) is the calculated weight, by means of mutual information gain, for the opcode oz and tfi,j is the sequence frequency measure for the given opcode sequence. We obtain a vector v composed of weighted opcode-sequence frequencies,
where osi is the opcode sequence and wtfi is the weighted term frequency for that particular opcode sequence.
Overview of LLGC
Learning with Local and Global Consistency (LLGC) [11] is a semi-supervised algorithm that provides smooth classification with respect to the intrinsic structure revealed by known labelled and unlabelled points. The method is a simple iteration algorithm that constructs a smooth function coherent to the next assumptions: (i) nearby points are likely to have the same label and (ii) points on the same structure are likely to have the same label [11].
Formally, the algorithm is stated as follows. Let
Rm be the set composed of the data instances and L = {1, …,c} the set of labels (in our case, this set comprises two classes: malware and legitimate software) and
the unlabelled instances. The goal of LLGC (and every
semi-supervised algorithm) is to predict the class of the unlabelled instances. F is the set of n x c matrices with non-negative entries, composed of matrices 
that match to the classification on the dataset X of each instance Xi. with the label assigned by
can be defined as
a vectorial function such as
to assign a vector Fi to the instances xi. Y is an n x c matrix such as
with Yi,j = 1 when xi is labelled as yi = j and Yi,j = 0 otherwise. Considering this, the LLGC algorithm performs as follows:
Fig. 1. LLGC algorithm
The algorithm first defines a pairwise relationship W on the dataset X setting the diagonal elements to zero. Suppose that a graph G = (V, E) is defined within X, where the vertex set V is equal to X and the edge set £ is weighted by the values in W. Next, the algorithm normalises symmetrically the matrix W of G. This step is mandatory to assure the convergence of the iteration. During each iteration each instance receives the information from its nearby instances while it keeps its initial information. The parameter a denotes the relative amount of the information from the nearest instances and the initial class information of each instance. The information is spread symmetrically because S is a symmetric matrix. Finally, the algorithm sets the class of each unlabelled specimen to the class of which it has received most information during the iteration process.
Empirical Validation
The research question we seek to answer through this empirical validation is the following one: What is the minimum number of labelled instances required to assure a suitable performance using LLGC?
To this end, we collected a dataset comprising 1,000 malicious executables and 1,000 benign ones. For the malware, we gathered random samples from the website VxHeavens, which has assembled a malware collection of more than 17,000 malicious programs, including 585 malware families that represent different types of current malware such as Trojan horses, viruses and worms. Although they had already been labelled according to their family and variant names, we analysed them using Eset Antivirus2 to confirm this labelling. For the benign dataset, we collected legitimate executables from our own computers. We also performed an analysis of the benign files using Eset Antivirus to confirm their legitimacy. Although we have already computed the IG values for the complete VxHeavens database, due to computational limitations in order to calculate the unique byte n-grams we have selected only 1,000 executables randomly to perform the final validation.
Hereafter, we extracted the opcodes-sequence representation for each file in the dataset for a sequence length of 2. Because the total number of features we obtained was high, we applied a feature selection step employing mutual information gain, selecting the 1,000 top ranked sequences.
Next, we split the dataset into different percentages of training and test instances the dataset. In other words, we changed the number of labelled instances from 10% to 90% to measure the effect of the number of previously labelled instances on the final performance of LLGC in detecting unknown malware.
We used the LLGC implementation provided by the Semi-Supervised Learning and Collective Classification package3 for the well-known machine-learning tool WEKA [13]. Specifically, we configured it with a transductive stochastic matrix W [11] and we employed the Euclidean distance with 5 nearest neighbours.
In particular, we measured the True Positive Ratio (TPR), i.e., the number of malware instances correctly detected divided by the total number of malware files: TPR = TP/(TP+FN) where TP is the number of malware cases correctly classified (true positives) and FN is the number of malware cases misclassified as legitimate software (false negatives). We also measured the False Positive Ratio (FPR), i.e., the number of benign executables misclassified as malware divided by the total number of benign files: FPR = FP/(FP + TN) where FP is the number of benign software cases incorrectly detected as malware and TN is the number of legitimate executables correctly classified. Furthermore, we measured accuracy, i.e., the total number of the hits of the classifiers divided by the number of instances in the whole dataset: Accuracy(%) = (TP+TN)/(TP+ FP + TP + TN) Besides, we measured the Area Under the ROC Curve (AUC) that establishes the relation between false negatives and false positives [14]. The ROC curve is obtained by plotting the TPR against the FPR.
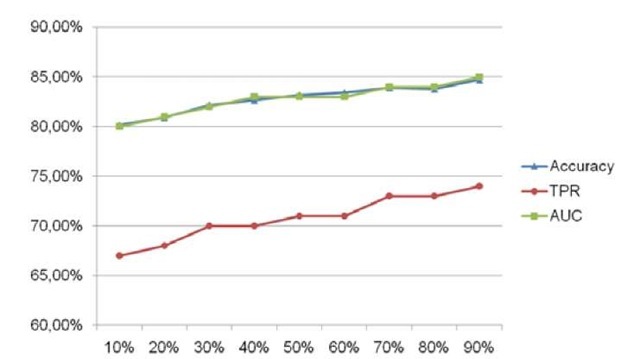
Fig. 2. Accuracy, TPR and AUC results. The X axis represent the percentage of labelled instances. The precision of the model increases along with the size of the labelled set.
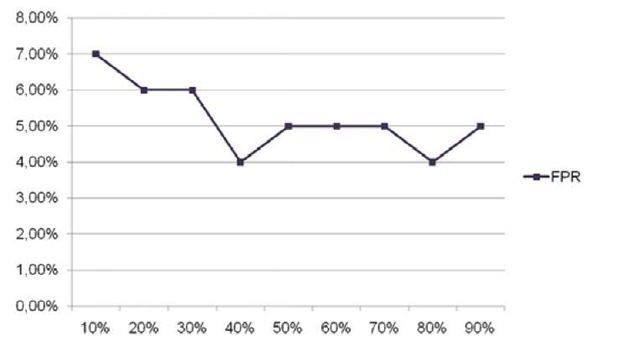
Fig. 3. FPR results. The X axis represent the percentage of labelled instances. The FPR decreases as the size of the labelled set increases. In particular, the best results were obtained with a size of the labelled dataset of 40%.
Fig. 2 and Fig. 3 show the obtained results. In particular, we found out that the greater the size of the labelled instances set the better the results. Specifically, the best overall results were obtained with a training set containing 90% of labelled instances. However, the results are above the 80% of accuracy and AUC when only the 10% of the instances are labelled. These results indicate that we can reduce the efforts of labelling software in a 90% while maintaining a accuracy higher than 80%. However ,the FPR are not as low as they should be, with a lowest value of 4% of false positives. Although for a commercial system this value can be too high, due to the nature of our method, which is devoted to detect new malware, this value is assumable.
We consider that these results are significant for the anti-malware industry. The reduction of the efforts required for unknown malware can help to deal with the increasing amount of new malware. In particular, a preliminary test with a Bayesian Network trained with Hill climber shows an accuracy of 86.73% which only a bit higher that the presented semi-supervised approach. However, because of the static nature of the features we used with LLGC, it cannot counter packed malware. Packed malware is produced by cyphering the payload of the executable and having it deciphered when finally loaded into memory. Indeed, broadly-used static detection methods can deal with packed malware only by using the signatures of the packers. Accordingly, dynamic analysis seems to be a more promising solution to this problem [15]. One solution for this obvious limitation of our malware detection method is the use of a generic dynamic unpacking schema such as PolyUnpack [16], Renovo [15], OmniUnpack [17] and Eureka [18].
Concluding Remarks
Unknown malware detection has become an important topic of research and concern owing to the growth of malicious code in recent years. Moreover, it is well known that the classic signature methods employed by antivirus vendors are no longer completely effective in facing the large volumes of new malware. Therefore, signature methods must be complemented with more complex approaches that provide the detection of unknown malware families. While machine-learning methods are a suitable approach for unknown malware, they require a high number of labelled executables for each classes (i.e., malware and benign datasets). Since it is difficult to obtain such amounts of labelled data in a real-word environment, a time-consuming process of analysis is mandatory.
In this paper, we propose the use of a semi-supervised learning approach for unknown malware detection. This learning technique does not need a large amount of labelled data; it only needs several instances to be labelled. Therefore, this methodology can reduce efforts in unknown malware detection. By labelling 50% of the software, we can achieve results with more than 83% accuracy.
Future work will be focused on three main directions. First, we plan to extend our study of semi-supervised learning approaches by applying more algorithms to this issue. Second, we will use different features for training these kinds of models. Finally, we will focus on facing packed executables with a hybrid dynamic-static approach.
