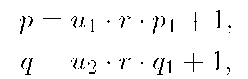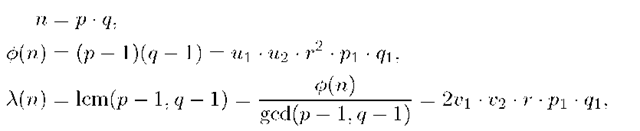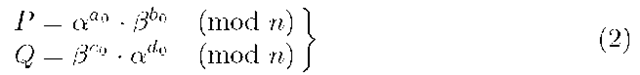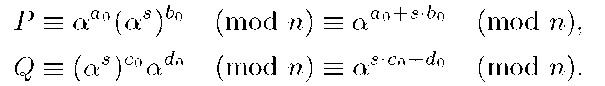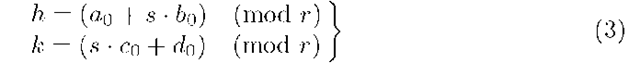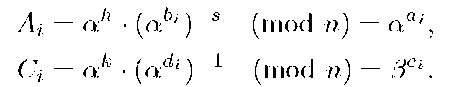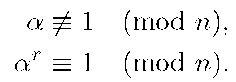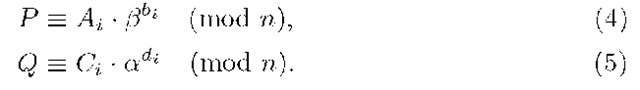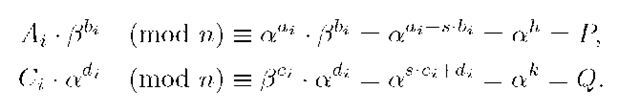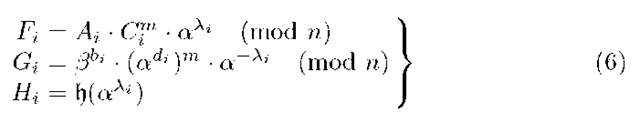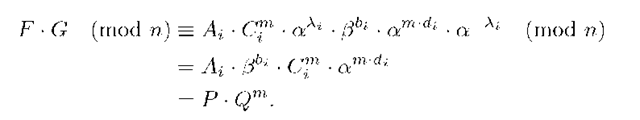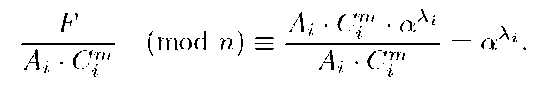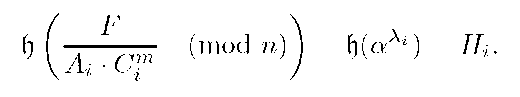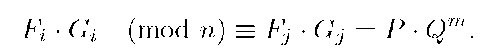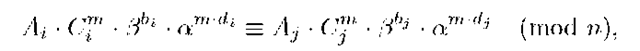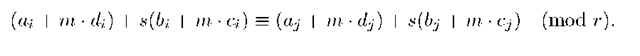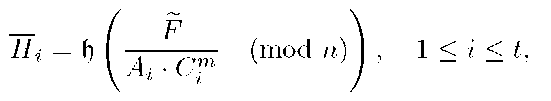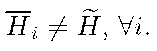Abstract
Group signature schemes allow a user, belonging to a specific group of users, to sign a message in an anonymous way on behalf of the group. In general, these schemes need the collaboration of a Trusted Third Party which, in case of a dispute, can reveal the identity of the real signer. A new group signature scheme is presented whose security is based on the Integer Factorization Problem (IFP) and on the Subgroup Discrete Logarithm Problem (SDLP).
Keywords: Digital signature, Group signature, Public key cryptography.
Introduction
As it is well-known, there are different protocols to determine digital signatures. In general, these protocols are based on public key cryptosystems [1,2,3]. The main characteristic of this signature schemes is that each signer has one public key and one private key.
Moreover, the procedures of digital signatures are made more efficient if hash functions are used [4]. The hash functions are public and they allow to sign a digest or hash of the message.
Group signature schemes were proposed by Chaum and van Heyst in 1991 [5]. These schemes permit a signer group to sign a given message such that only a member of the group computes the signature on behalf of the whole group. A Trusted Third Party (T) collaborates in the generation of the keys and is able to reveal the identity of the user who signed the message, if a dispute arises. The main characteristics defining the group signatures are the following:
1. Only a member of the signer group signs the message.
2. The receiver of the message can verify that the signature of the message was generated by a member of the signer group, but he cannot determine which member of the group was the signer.
3. If a dispute arises, it is possible to open the signature in order to determine who was the actual signer of the message.
Group signatures can be understood as an extension of credential authentication and membership authentication schemes. In the first schemes, a user proves that he belongs to a specific group [6]; whereas in the second ones, a member of a group can convince a verifier that he belongs to that group without revealing him his identity [7,8].
There exist several proposals for group signatures, which use a number of cryptographic primitives. Some of these proposals need a Trusted Third Party (TTP), T, at least for the initialization process. Other schemes, however, allow any user to create the group he chooses to belong to.
As a general rule, group signatures make use of schemes whose security is based on computationally-intractable mathematical problems [9,10,11]. Typically, such problems are the Integer Factorization Problem (IFP) and the Discrete Logarithm Problem (DLP).
Nevertheless, most of these protocols show some limitations. For example, the schemes described in [12,13,14] have a security problem [15]. Moreover, the security of the schemes presented in [16,17] is tested under artificial and unlikely conditions [18].
The proposed group signature scheme presented here guarantees that a true group signature is generated for a given message. Moreover, the scheme improves existing protocols in terms of user friendliness, computational efficiency, time and band-width saving. Moreover, this proposal verifies the properties required for group signature schemes: Only a group member can validly sign a document or message. The signed-message receiver is able to verify that the signature is a valid group signature, i.e., it has been carried out by one legitimate member of the group. However, the receiver will not be able to determine which particular group member actually signed the message. Finally, if required (in case of a dispute, for example) it is possible to disclose the signer, i.e., to reveal which user actually signed the message.
The rest of this paper is organized as follows: In section 2 a group signature scheme based on the Integer Factorization and Subgroup Discrete Logarithm Problems is proposed. In section 3, the main properties of the new scheme are shown. The security analysis of the proposal is performed in section 4, and finally, the conclusions are presented in section 5.
A Group Signature Scheme Based on IFP and SDLP
In this section we propose a group signature scheme for which a randomly chosen member of a given group signs a document, on behalf of the whole group, making use of his private key. The verifier of the signature checks whether or not the signature corresponds to one of them, using the public key that all the members of the group share. Moreover, the verifier will not be able to decide who was the original signer.
Let G = {Ui,U2,… ,Ut} be the signer group and let T be the Trusted Third Party.
Setup Phase
In this phase, T generates its pre-key, the public key shared by the group, as well as helps the members of G to generate their private keys [19].
Pre-key generation. T generates its pre-key as follows: 1. T chooses two large primes p and q, such that
where r,p1,q1 are prime numbers,
with gcd(ui,u2) = 2, that is, u\ = 2vi, u2 = 2v2, and gcd(v1 ,v2) = 1.
In order to guarantee the security of the scheme, the bitlength of r is selected so that the Subgroup Discrete Logarithm Problem (SDLP) of order r in Z* be computationally infeasible. 2. T computes
where
is the Euler function,
is the Carmichael function, and lcm represents the least common multiple.
Then, T selects an element
with multiplicative order r modulo n, such that
Note that this element, a, can be efficiently computed as T knows the factorization of n and consequently it knows
[19, Lemma 3.1]. We denote by Sr the subgroup of Z* generated by a. 3. T generates a secret random number
and determines
4. T publishes the values (a, r, f3, n); whereas it keeps secret the values of (p, q, s).
With the previous hypothesis, the security of T’s secret, s, is based on the Integer Factorization Problem (IFP) and on the Subgroup Discrete Logarithm Problem (SDLP).
Key generation. In order to determine the private keys of the members of G, T computes its private key and the public key which will be shared by all the signers of G.
To do this, T generates four random numbers
as its private key and determines the shared public key for G by computing
From (2), we have
that is, there exist integers
Hence,
that is, there exist integers 
such that
In order to guarantee that T cannot impersonate any user of G, an interactive session between each user Ui and T is necessary to determine the private key of 
Hence, the following interactive protocol is developed:
1. Ui generates two secret integers
at random and sends to T the values of
in a secure way for protecting both secret integers.
2. T computes
From (3), T can compute Ai,Ci since it knows h,k,abi, and adi, but it cannot compute ai,ci because it cannot solve the SDLP. Then T sends to Ui the values of Ai, Ci by using a secure channel. 3. The private key of Ui is the set (bi,di,Ai,Ci). Note that for Ui is also impossible to compute the values of ai,ci.
Remark. Note that T knows two values of the U’s private, Ai,Ci, but it is impossible for it to know the rest of that key. Moreover, for both Ui and T it is impossible to compute the values ai: ci because they are protected by the SDLP.
Key verification. For verifying the pre-key of T, each members of the signer group,
must check
Moreover, each signer,
must verify that his private key corresponds to the shared public key, i.e., must check if it holds:
In fact:
Group Signature Generation
Let M be the message to be signed by a member of G. We can assume that after computing its hash value (by using, for example, a public hash function from the SHA-2 family), we have (j(M) = m. For signing M on behalf of the group G, a random and anonymous member of G is chosen, for example, Ui. Next, U\ does the following.
1. Ui generates a secret integer
at random. This value must be generated each time a message is signed.
2. Ui determines his signature, (Fi,Gi,Hi), for M, computing the following values:
3. Finally, T publishes the group signature for the message M: (F, G, H) = (Fj, Gj,Hi).
Remark. Nobody can impersonate the user Ui because he is the only one knowing the values bi,di, and Xi.
Group Signature Verification
Let (F, G, H) be a group signature of G for the message M. In order to verify this signature, any verifier knowing the public key of the group G, (P,Q), can check that
The equation (7) can be immediately justified from expressions (4)-(6) as follows:
Properties of the New Scheme
The proposed scheme has the following properties:
1. All the operations involved in the different phases described in the previous paragraphs can be efficiently computed in polynomial time.
2. Despite T knows part of Ui’s private key, it cannot forge the signature determined by Ui as the signer has generated at random the value: Xi. Nevertheless, it can generate a valid group signature.
3. The verifier is only able to test whether the signature was generated by a member of the signer group and it is not able to ascertain the identity of the actual signer.
4. In case of dispute, T can disclose the signer since it knows part of the private key of each member of G.
In fact, as T knows the values of Ai and Ci of the signer Ui, by using the equations in (6) defining the group signature, it can compute
Then, T can prove, without the collaboration of Ui, that
Security Analysis
Moreover, the scheme is secure as no member of G, say U, knowing only his own private key, (bi,di,Ai,Ci), and the shared public key,
can determine neither the secret value s of T, nor its private key (ao, bo, co, do).
In fact, determining s from a and
see formula (1), means solving the discrete logarithm problem in the subgroup Sr, of order r generated by a, which is impossible as the size of r was chosen such that the SDLP was unfeasible to solve, and moreover, the factorization of n is infeasible as well.
Moreover, the private key of T was generated at random and it is only known that it verifies the equation (2), but computing any of the values of this key implies solving the DLP in Z* .
It is also impossible for any Ui to determine the values of h = ai + s • bi, and k = s • ci + di, as he only knows bi,di,aai,@ci. In all cases, it is necessary to solve a discrete logarithm problem.
Furthermore, two members of G, say Ui and Uj, could conspire and try to compute any of the secret values of T: s,h,k,a0,b0,c0,d0, or generate a false signature for the group. To carry out any of these attacks, both could generate their signatures for a message, say (Fi,Gi,Hi) and (Fj,Gj,Hj), respectively. Then, from the verification identity (7), they have
Hence, they obtain
or equivalently,
and as a has order r modulo n, it results
that is, they could obtain
Nevertheless, none of them know the values of
so they cannot compute s.
Finally, nobody is able to forge a group signature for the message M without this fact being detected and proved by T. In fact, a forger could know the public key, (P, Q), the message, M, its hash, m, and the values
From these data, the forger can choose an element
determine the value
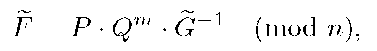and publish the set
for a hash value
as a group signature for the message M, that passes the verification equation (7).
Nevertheless, T can prove that this group signature is a forgery by computing
and showing that 
Conclusions
A new group signature scheme has been proposed. The security of the scheme is based on two difficult problems from Number Theory: Integer factorization and subgroup discrete logarithms (and the DLP in the key generation).
The scheme verifies the properties required for general group signature schemes. Any single member of the signer group is able to sign the message. The receiver of the message can verify that the signature of the message was generated by a actual member of the signer group, but he cannot determine which member of the group was the signer. If a dispute arises, a Trusted Third Party can open the signature and determine who was the signer of the message.
The group signature scheme is efficient since the computations only require polynomial time and moreover it is secure against conspiracy attacks and against forgery.
