Scanners (Compiler Writing) Part 4

EQUIVALENCE OF REGULAR GRAMMARS AND FINITE-STATE ACCEPTORS

The equivalence of regular grammars and finite-state acceptors is shown in this section. First, a method for constructing an NFA from a regular grammar is given. Then a way of converting a DFA to a regular grammar is illustrated, completing the proof that the languages accepted by finite-state acceptors are the same as the languages which can be produced by regular grammars.

The following theorem and proof provide the procedure for converting a regular grammar to a nondeterministic finite-state acceptor.

Theorem 4-3 There exists a nondeterministic finite-state acceptor F = (K, VT, M, S, Z) which accepts the language generated by the regular grammar

Proof Define the NFA F with the states of F beingwhere

The initial state of the acceptor is £ (the start symbol of the grammar), and its final state is X. For each production of the grammar, construct the mapping M from $ in the following manner:

1.if there is a production

2.if there is a production

The acceptor F, when processing sentence x, simulates a derivation of x in the grammar G. It is necessary to show that L(F) = L{G). Let be in the language L(G). Then there exists some derivation in G such that for a sequence of nonterminalsFrom the construction of M, it is clear that M(S, a:) containscontains A2,…, and contains X. Therefore,since M(S, x) contains X and

Conversely, ifa derivation of G which simulates the acceptance of x in F can be easily obtained, thereby concluding that

To illustrate how an NFA is constructed from a regular grammar, consider the grammarwherethe set of productions $ are:

and which generates strings of the formDefine

an and M is given by

Then F is a nondeterministic finite-state acceptor which accepts the language represented by the regular grammar G.

Just as a nondeterministic finite-state acceptor can be constructed from a regular grammar in a straightforward manner, a regular grammar also can be derived from a deterministic finite-state acceptor in a simple way. The following theorem, like the previous theorem, furnishes the procedure needed to construct a regular grammar.

Theorem 4-4 There exists a regular grammarwhich produces the language accepted by a given deterministic finite-state acceptor

Proof Define the regular grammar G with the states of K being the nonterminals of G. The starting symbol of G is S (the starting state of F), and the set of productions are defined as:

It must be shown thatif and only ifIn the case ofadd the production

LetThen there is the set of transitions:

where A„ is a final state of F. Thus G contains the productions

and the grammar G can produce strings accepted by F.

Conversely, if, then an acceptance of x in F which simulates a derivation in G can be easily obtained, thereby concluding that

To illustrate the conversion of a deterministic finite-state acceptor to a regular grammar, consider the acceptorwhere the mapping function is given in Table 4-9. This DFA accepts strings which have an even number of Os and Is. Using the method for constructing a regular grammar as given in Theorem 4-4, the grammar G is defined as G = ({5, A, B, C}, {0,1} S, where <E> is defined as

Table 4-9

State		Input
	0	1
S	B	A
A	C	S
B	S	C
C	A	B

Because S is a final state, wherever a production of the form a -* {iS occurs, the production a /? is also included in The production 5 -» e is also in $ because SeZin the DFA.

Because nondeterministic finite-state acceptors are equivalent to deterministic acceptors, the equivalence of finite-state acceptors to regular grammars has been established by Theorems 4-3 and 4-4. Thus regular grammars may be used to represent scanners which are implemented as finite-state acceptors. However, regular expressions are more easily used to depict scanners, and demonstrating the equivalence of regular expressions to finite-state acceptors is the topic of the next section.

EQUIVALENCE OF REGULAR EXPRESSIONS AND FINITE-STATE ACCEPTORS

Regular expressions, which were introduced in Sec. 4-3, are often used as a convenient way of describing scanners. The importance of this will become evident in the next section when a scanner generator which uses regular expressions as input is presented. This section details the methods for generating a finite-state acceptor from a regular expression or turning a finite-state acceptor into a regular expression. In so doing, it will be shown that regular expressions and finite-state acceptors are equivalent. After recalling the theories of the previous section, it then can be seen that the languages which can be derived from regular grammars and regular expressions are the same.

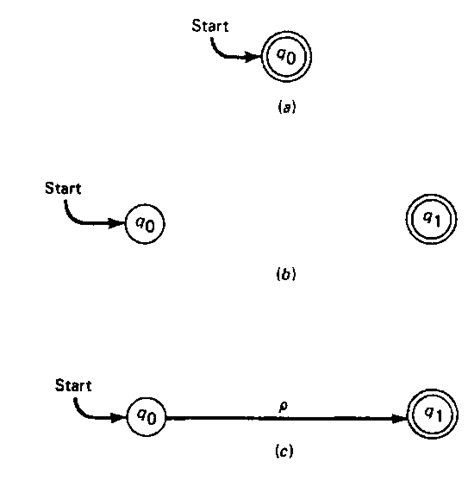
It is conceptually easier to understand how a regular expression can be converted to a finite-state acceptor by using a transition diagram. Before proceeding, however, it is useful to show how the three regular expressions e, </>, and p, where p e Vr, are represented in a transition diagram. Figure 4-10 illustrates the finite-state diagrams associated with each of these expressions. The expression e is drawn in Fig. 4-10a and indicates that no state transition occurs on empty input (e-transitions will be included later). Figure 4-106 indicates that the regular expression does not accept any input string, including e, and the transition that occurs with the regular expression p is exhibited in Fig. 4-10c.

With the transition diagrams of Fig. 4-10 representing the most simple regular expressions, more complex regular expressions can be developed using the operations of alternation, concatenation, and closure.

Figure 4-10 Transition diagrams for the regular expressions e, <#>, and p.

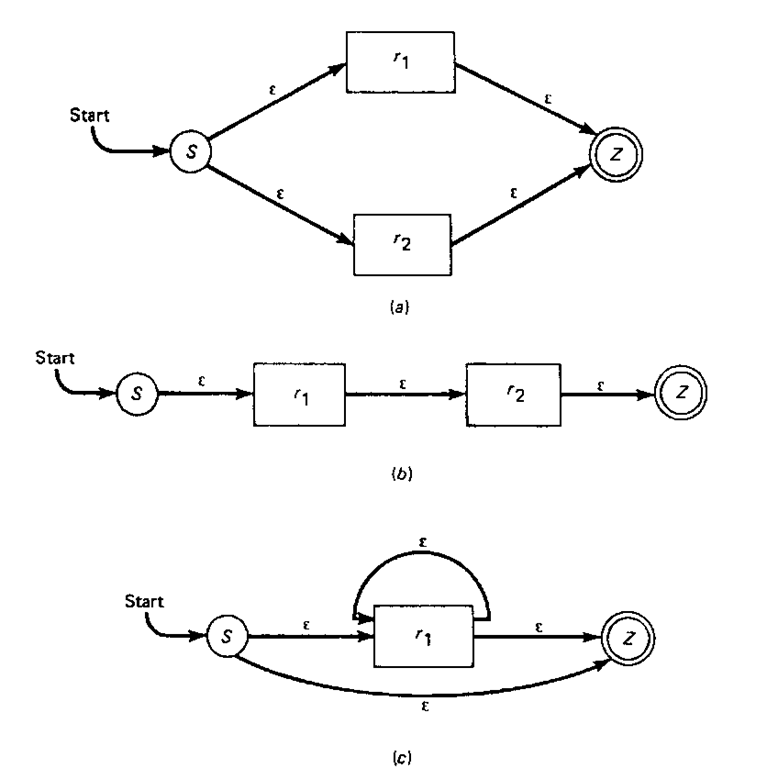
Figure 4-11 illustrates how two regular expressions, and r2, may be represented by an NFA with e-transitions when one of the operations is applied. In each case, a new starting state 5 and a new final state Z have been created, both of which are states separate from the finite-state acceptors representing rj and r2. An arc leading into an expression r1 or r2 represents a transition to the starting state of the FSA representing that expression, while the arc leading out of the FSA for an expression depicts a transition from the final state of the acceptor to the next state.

The transition diagram for the expression rx\r2 is given in Fig. 4-1 la. As the acceptor must accept one of rx and r2, e-transitions from the starting state to the FSAs for rx and r2 are drawn. Concatenation, which is illustrated in Fig. 4-11 b for the expression rxr2, makes an e-transition from rx to r2 necessary as well as one from the starting state to rl and r2 to the final state. Figure 4-1 lc depicts the FSA for the expression {r,}. The e-transition from the final state of rx to its starting state permits more than one repetition of rx by the finite-state acceptor. Zero occurrences of the expression are allowed with the e-transition from the starting state S to the final state Z.

Figure 4-11 Transition diagrams for the expressions

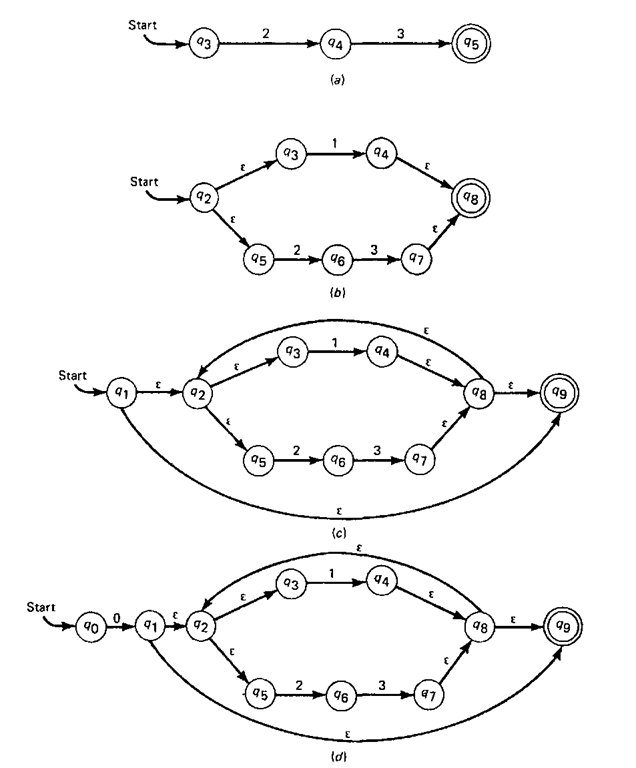
To demonstrate how the rules for constructing an NFA with e-transitions from a regular expression may be applied, the regular expression 0{1 [23} is used. Figure 4-12 illustrates the steps involved in creating the acceptor from this expression. By rewriting the expression in a fully parenthesized form, the order of evaluation becomes more evident and the finite-state acceptor can be created in a step-by-step manner starting with the operators to be evaluated first. Hence the expression can be written as 0{1|(23)}. With the terminal symbols of the expression being the set {0,1,2,3}, the first operation to be performed is the concatenation of the two subexpressions 2 and 3.

Figure 4-12 Creation of an NFA with E-transitions.

The finite-state acceptor for the resulting expression 23 is created as shown in Fig. 4-12a. Then the alternation operator is applied to the two subexpressions 1 and 23, resulting in the finite-state acceptor of Fig. 4-126. Figure 4-12c gives the finite-state acceptor for the expression (1|(23)} once closure has been applied to the preceding expression. Finally, the zero concatenated with the expression of Fig. 4-12c gives the entire regular expression, and the finite-state acceptor which is produced is given in Fig. 4-12^. For simplicity, several e-transitions in Fig. 4-12a were eliminated.

Theorem 4-5 Given a regular expression R, there exists an NFA with e-transitions, F, which accepts the language generated by R.

Proof Only an outline of the proof is given to sketch how an NFA with e-transitions is constructed.

The proof is done by induction on each of the three operators found in regular expressions. In the case of alternation in which the FSAs for the two subexpressions rx and r2 are , respectively, a new FSAis defined as follows:> and the setsare all disjoint. Then the mapping function is defined aswith the following mappings also given:

For concatenation, the new FSA is defined aswhere K and VT are the same as with alternation, and the mapping function is defined aswith the mappings

also included withClosure requires a new acceptor which is created from the original acceptor

has the same mappings as M but with the additions

It is shown by induction that with the application of an operator to the regular expressions as just described, the newly created finite-state acceptor accepts the same language as is generated by the expression resulting from the application of the operator.

Using the regular expression 0(11 (23)} from the previous example, an FSA can be derived aswhere the mapping function is defined in Table 4-12. This NFA with e-transitions is created by the application of the rules of construction given in the preceding proof to the expression starting with the most nested operators, as was done when transition diagrams were used in the previous example.

Table 4-12

State			Input
	0	1	2	3	e

The combination of the previous and following theorem will establish the equivalence of regular expressions and finite-state acceptors. Because FSAs and regular grammars are also equivalent, it can be seen that regular grammars and regular expressions are equivalent.

Theorem 4-6 Given a deterministic finite-state acceptor which accepts the language L, there exists a regular expression which denotes L.

Proof As was the case with the previous theorem, only an outline of the proof is given.

For the DFAis defined to be the set of all strings x such that ~and for any prefix of x, say, y, but not including x or e, thenThusis the set of all strings taking the acceptor from state qt to state ^ without reaching a state numbered greater than k. Thencan be recursively defined as follows:

It is then shown by induction that for all /’, j, and k, a regular expression denoting the languagecan be found, starting withas the basis. Finally, the language L accepted by F can be represented aswhere the largest state of F is qn. Thus the regular expression is given by where

are final states of F.

Figure 4-13

The proof of Theorem 4-6 provides the procedure for finding a regular expression which denotes the language accepted by a DFA. Notice that the equation

can be represented by the regular-expression equation

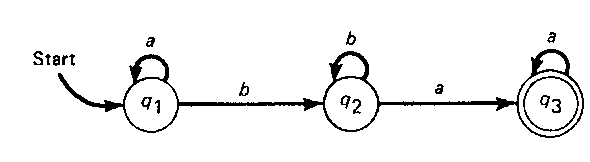
An example should illustrate how this method can be used to create a regular expression. The transition diagram of a DFA which accepts strings of the form

is given in Fig. 4-13. The values of allfor this DFA are listed in Table 4-13 after they have been simplified. The first column of the table, with k = 0, requires that an intermediate state cannot be greater than q0. As the smallest state is qx, any expressioncan only generate a single character or an intermediate state would be required in going from state q, to state qr The expression canalso be the empty string if qt and q} are the same state. Thus the expressioncan be either the empty-string expression or the expression a, andcan be the expression b. The expressionwhere k is 1, 2, or 3, gives the expression {a}. Only qx can be an intermediate state if qx is also to be the end state. The expression foris {a}b because only qx can be an intermediate state. For the expressionsthe expression {a}b{b} is derived as intermediate states qx and q2 are allowed. The expressions are the same, since q3 cannot be an intermediate state if q2 is the end state. As the only final state for this DFA is q3, the regular expression for the DFA is

Table 4-13

k	0	1	2	3

To illustrate further how some expressions r(* are derived and simplified, the following examples are given:

This section has shown that regular expressions and finite-state acceptors both represent the same class of languages. Methods of converting from one form to the other also were described. The next section uses regular expressions to describe scanners for a scanner generator.