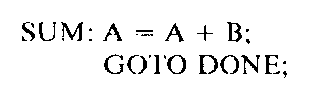The analysis of a source program during compilation is often complex. The construction of a compiler can often be made easier if the analysis of the source program is separated into two parts, with one part identifying the low-level language constructs (tokens) such as variable names, keywords, labels, and operators, and the second part determining the syntactic organization of the program. This topic discusses the first and easier of the two analyzers, the lexical analyzer or scanner, which was introduced in Chap. 1.
Two aspects of scanners concern us. First we describe what the tokens of the language are. The class of regular grammars, introduced in Chap. 2, is one vehicle which can be used to describe tokens. Another description approach which is briefly introduced involves the use of regular expressions. Both description methods are equivalent in the sense that both describe the set of regular languages.
The second aspect of scanners deals with the recognition of tokens. Finite-state acceptors are devices that are well suited to this recognition task primarily because they can be specified pictorially by using transition diagrams.
Section 4-1 describes the requirements of a scanner. Based on these requirements, Sec. 4-2 presents an elementary scanner design and its implementation. Regular expressions and regular grammars are dealt with in Sec. 4-3. Section 4-4 deals with deterministic and nondeterministic finite-state acceptors, including nondeterministic acceptors with e-transitions. The equivalence of regular grammars and finite-state acceptors and the equivalence of regular expressions and finite-state acceptors are shown in the next two sections. Methods of converting from an acceptor to a regular grammar or a regular expression and vice versa are also examined. These notions, in addition to being useful in understanding scanner generators, are also useful in gaining insight into higher-level syntax analyzers such as LR(1) and LALR(l) parsers, which are discussed in Chap. 7. The topic concludes with a presentation of a scanner generator.
Sections 4-1 and 4-2 contain an elementary, nonautomated approach to scanner generation. The reader who is not interested in scanner generators on first reading need not read the remainder of this topic. A scanner generator is a system which automatically generates a scanner for a particular language, given the description of the tokens for that language. Readers who intend to study LR parsers in Chap. 7 are advised to study Sec. 4-4.
THE SCANNING PROCESS
The scanner was briefly introduced in topic 1. This section elaborates on the scanning process, that is, what the scanner does in relation to the entire compilation process.
The scanner represents an interface between the source program and the syntactic analyzer or parser. The scanner, through a character-by-character examination of the input text, separates the source program into pieces called tokens which represent the variable names, operators, labels, and so on that comprise the source program.
As was mentioned in topic 1, the parser usually generates a syntax tree of the source program as defined by a grammar. The leaves of the tree are the terminal symbols of the grammar. It is these terminal symbols or tokens which the scanner extracts from the source code and passes to the parser. It is possible for the parser to use the terminal character set of the language as the set of tokens, but since tokens can be defined in terms of simpler regular grammars rather than the more complex grammars used by parsers, it becomes desirable to use scanners. Using only parsers can become costly in terms of execution time and memory requirements, and complexity and execution time can be reduced by using a scanner.
The separation of lexical analysis (scanning) and syntactic analysis can also have other advantages. Scanning characters is typically slow in compilers, and by separating it from the parsing component of compilation, particular emphasis can be given to making the process efficient. Furthermore, more information can be made available to the parser when it is needed. For example, it is easier to parse tokens such as keywords, identifiers, and operators, rather than tokens which are the terminal character set (i.e., A, B, C, etc.). If the first token for a DO WHILE statement is DO rather than just ‘D’, the compiler can determine that a repetition loop is being parsed rather than other possibilities such as an assignment statement.
The scanner usually interacts with the parser in one of two ways. The scanner may process the source program in a separate pass before parsing begins. Thus the tokens are stored in a file or large table. The second way involves an interaction between the parser and the scanner. The scanner is called by the parser whenever the next token in the source program is required. The latter approach is the preferred method of operation, since an internal form of the complete source program does not need to be constructed and stored in memory before parsing can begin. Another advantage of this method is that multiple scanners can be written for the same language. These scanners vary depending on the input interfaces used in the language. Throughout this topic, the scanner will be assumed to be implemented in this manner. In most cases, however, it makes little difference how the scanner is linked to the parser.
As mentioned earlier, the scanner breaks the source program into pieces called tokens. The type of token is usually represented in the form of a unique internal representation number or integer. For example, a variable name or identifier may be represented by the number 1, a constant by 2, a label by 3, and so on. The token, which is a string of characters (or a value in the case of a constant), is often stored in a table. Thus the values of constants are stored in a constant table while variable names are stored in a symbol table for variables. The scanner then returns the internal type of the token and sometimes the location in the table where the token was stored. Not all tokens may be associated with a symbol or constant table location. While variable names and constants are stored in a table, operators, for example, may not be. The scanner might return a unique token or internal representation number for each operator. Conversely, one internal representation number might represent the entire class of operators and the scanner would also return the particular operator by making reference to this operator in an operator table. Note that the strategy of assigning a unique representation number for each member of a class is not possible for classes such as identifiers because the number of identifiers is not known in advance. Furthermore, later syntactic and semantic processing often associates other information with these identifiers, and this information would be stored in the symbol table (see Chap. 8). Such information might involve a variable’s type and address.
As an example of the values returned by a scanner, assume that the representation number of a variable name has a value of 1, a constant a value of 2, a label a value of 3, a keyword a value of 4, the addition operator a value of 5, the assignment operator a value of 6, and so on. Labels and variable names are appended to the identifier table and constants to the constant table. Assume that such insertions are done in sequential order. Also assume that if a token such as an operator is not associated with a table, then zero is returned for the location. Then the PL/I statements
would have the following items returned by the scanner:
|
Token |
Internal representation number |
Location |
|
SUM |
3 |
1 |
|
11 |
0 |
|
|
A |
1 |
2 |
|
= |
6 |
0 |
|
A |
1 |
2 |
|
-f |
5 |
0 |
|
B |
1 |
3 |
|
12 |
0 |
|
|
GOTO |
4 |
0 |
|
DONE |
3 |
4 |
|
12 |
0 |
Notice in this example that blanks are suppressed by the scanner. More will be said about blank suppression shortly. The advantage of using this method for returning the representation number from the scanner is that all representation numbers returned are of a fixed size. Furthermore, it is more efficient for the parser to work with integer values representing the symbols rather than the actual variable-length strings.
Some features that are available in a language have no syntactic meaning yet are included to improve human readability. For example, blank characters are allowed anywhere in FORTRAN but are to be ignored by the compiler. The scanner should recognize these constructs and ignore them by passing the next token to the parser which is not one of these types.
Having examined the scanning process and some of its requirements, we now turn our attention to the design and implementation of a simple scanner.
AN ELEMENTARY SCANNER DESIGN AND ITS IMPLEMENTATION
As described in the previous section, the main purpose of the scanner is to return the next input token to the parser. To be able to return a token, the scanner must isolate the next sequence of characters in the source text which designates a valid token. To do this, the scanner must also edit the source program, removing information such as comments, blanks, line boundaries, and whatever else is not important to the parsing and code-generating phases of the compiler. The scanner must identify the complete token and sometimes differentiate between keywords and identifiers. Furthermore, the scanner may perform symbol-table maintenance, inserting identifiers, literals, and constants into the tables after they have been converted to an internal form. Note that such symbol-table operations are sometimes performed later in the compilation process, rather than at scanning time. This subsection is concerned with the design and implementation of a scanner to perform these tasks.
Tokens can be described in several ways. One way of describing tokens is by using a regular grammar (see Sec. 2-3). Using this method of specification, generative rules are given for producing the desired tokens. For example, the regular grammar
contains the rules for generating the set of natural numbers.
Recall, however, that a scanner must recognize tokens. With this in mind, we investigate the possibility of describing tokens in a recognitive rather than generative manner. Describing tokens by means of how they can be recognized (or accepted) is often done in terms of a mathematical model called a finite-state acceptor.
In the remainder of this section we shall describe a set of tokens by specifying an acceptor which will recognize that set. Although regular grammars can also be used for this purpose, their application to scanner writing is delayed until the next section.
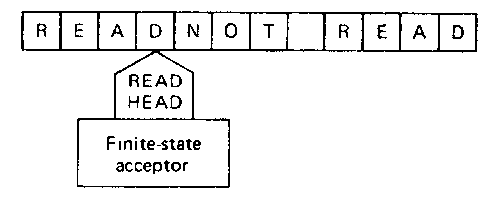
We first introduce the concept of a finite-state acceptor as a machine. The discussion here will be rather informal. A more formal and detailed discussion of this machine is given in Sec. 4-4. A finite-state acceptor (FSA) or finite automaton may be thought of as a machine consisting of a read head and a finite state control box. The machine reads a tape one character at a time (from left to right), as shown in Fig. 4-1. There are a finite number of states that the FSA can be in. A change in state occurs in the machine whenever the next character is read.
Whenever an FSA begins reading a tape, it is always in a certain state designated as the starting state. Some of the states the acceptor may be in are called final states, and if the acceptor attempts to read beyond the end of the tape while in a final state, the string which was on the tape is said to be accepted by the FSA. In other words, the string belongs to the language which is accepted by the FSA.
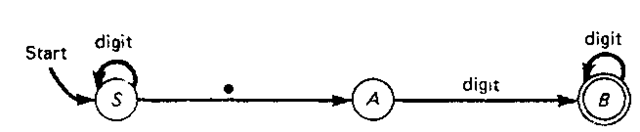
Finite-state diagrams or transition diagrams are often used to pictorially represent an FSA. An example of such a diagram is illustrated in Fig. 4-2. The FSA which is represented in the diagram accepts decimal real numbers which have at least one digit after the decimal point. The nodes of the finite-state diagram represent the states of the FSA, and in Fig. 4-2, the states are named S, A, and B.
Figure 4-1 A finite-state acceptor.
The arcs leading from one state to another indicate the state transitions. with the characters immediately above or beside the arcs denoting the input characters which cause this state transition. The arrow and the word "start" signify which state of the FSA is the starting state. In Fig. 4-2, the starting state is S. The nodes that consist of a pair of concentric circles are final states. In Fig. 4-2, only state B is a final state.
The behavior of the FSA in Fig. 4-2 is easily demonstrated. Assume that the tape the FSA is reading contains the string 12.75. The FSA begins in state 5, the starting state, and it remains in this state as each digit in the string preceding the decimal point is read. When the decimal point is read, the FSA changes to state A, and then it changes to state B when the first digit (i.e., 7) following the decimal point is read. The FSA then reads the next digit (5) and remains in state B. As the end of the tape has now been reached, the FSA terminates in the final state B and accepts the given decimal number as being valid.
If the FSA had not been in state B after a string had been read, the string would have been rejected. The string 12. is such a case. Rejection may also occur if no transition is designated at a certain state for some character that has been read. In the FSA of Fig. 4-2, this would occur if the FSA was in state S, state A or state B and, say, an alphabetic character had been read. Examples of strings which would be rejected for this reason are A15.1 and 12.B75.
The FSA that was used in this example of a finite-state diagram is called a deterministic finite-state acceptor. A formal definition of this type of acceptor is the topic of Sec. 4-4.
As a second example of an acceptor, consider the transition diagram of Fig. 4-3 which accepts the set of PL/I variable names. The acceptor contains the two states 5 and A, with the first being the start state and the second the final state. Notice the label of the arc in state A. The acceptor remains in state A if it reads any letter or digit or a special character from the set {#,@, $, _).
As a final example, let us consider a more complex example of a scanner. Again the scanner will take the form of a finite-state diagram. It is useful to name the tokens in the diagram once they are identified (which would be at a final state) and to include some processing information to improve the comprehensibility of the diagram.
Figure 4-2 A finite-state diagram for a decimal number.
Figure 4-3 A finite-state diagram for Pt./I variable name.
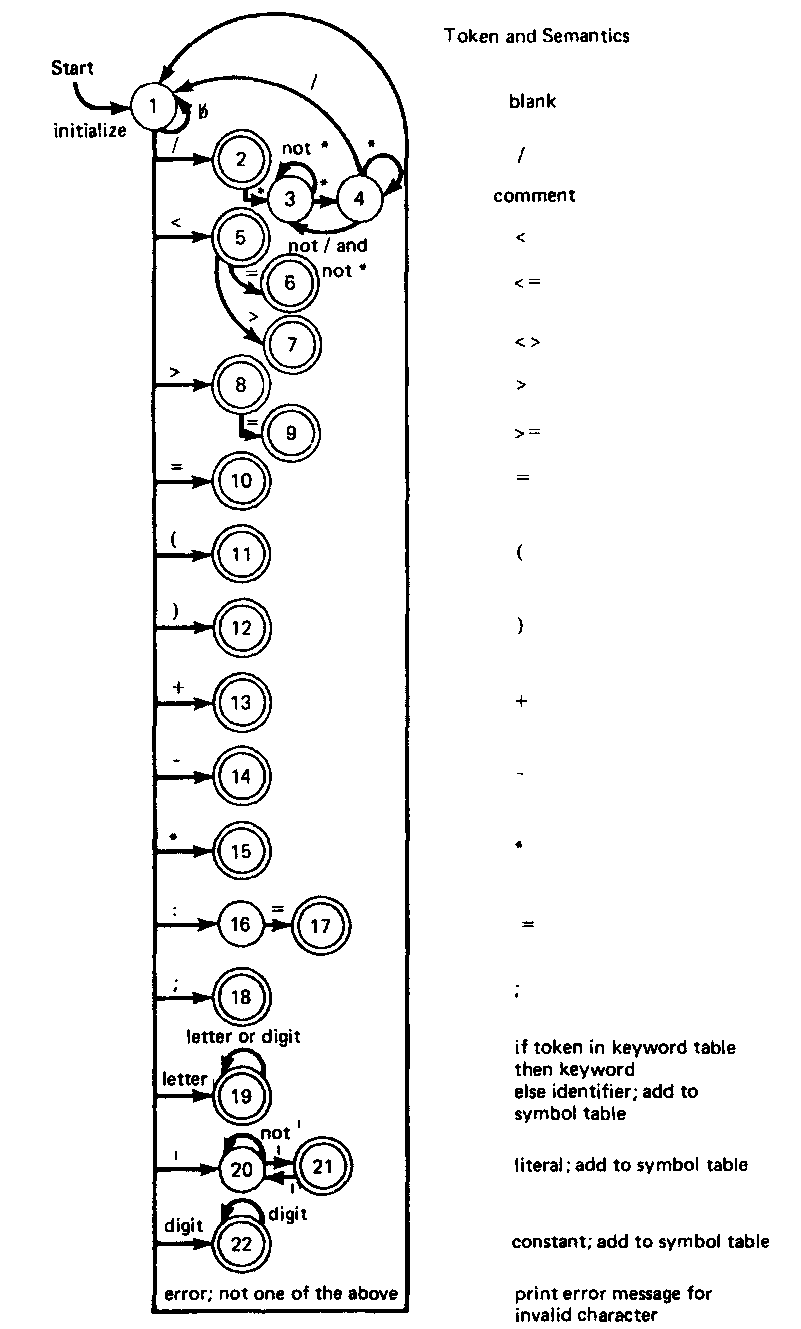
Figure 4-4 depicts the finite-state diagram for a language which consists of the tokens![]()
(assignment), ;, identifiers, keywords, constants, and literals (which are enclosed in apostrophes). Comments, which begin with a /* and end with a */, and blanks are ignored by the scanner, in the sense that they are treated simply as token separators.
A few things should be pointed out about this finite-state diagram. An arc which is labeled with a "not" preceding a character indicates that all input characters other than the one listed can cause the indicated state transition. The arc labeled "error" indicates that an invalid character has been found in the source text and that it cannot appear in any token except inside comments and literals. Furthermore, the scanner uses the longest input string possible for determining the token. Thus the character sequence "<=" is considered one token rather then two.
How the finite-state acceptor of Fig. 4-4 identifies tokens deserves some comment. States 5, 6, and 7 are used to recognize the tokens < , <= , and < > from the input string. If neither of the characters = or > follows the character < , then the acceptor ends up in the final state 5, indicating that the token is < . Otherwise the token <= or < > is determined as the acceptor ends up in either state 6 or state 7, respectively. Similarly, states 2, 3, and 4 are used for finding comments and the token /. If an asterisk follows the slash, all characters following the / * and until the one following the next * / are considered to be a part of the comment. Because a comment is not to be returned as a token to the parser, the scanner returns to the starting state immediately after scanning the comment so that the next token can be identified.
States 19 and 22 are used to recognize identifiers and integer constants, respectively. Identifiers begin with a letter and consist of all alphanumeric characters which follow. Constants are comprised of all digits until the next nonnumeric character is read. States 20 and 21 identify string literals. Literals begin and end with an apostrophe (‘) with the final state 21 designating the end of the literal. Because two consecutive apostrophes are used to represent a single apostrophe as a character within the string, a transition from state 21 to 20 occurs when this is the case.
The scanner depicted in Fig. 4-4 ignores blanks and comments and returns to the starting state whenever one of these types has been read. Blanks and comments are still used as separators, however, because the end of some tokens occurs whenever a character which cannot be included as part of that token is read. This occurs for constants when a blank follows a series of digits. In order to determine the end of some tokens, it is necessary to read one character beyond the end of that token.
Notice also that in Fig. 4-4, keywords and identifiers are detected in the same manner; however, a search of the keyword table is necessary to determine whether the token is a keyword or an identifier. This is indicated in the semantic description given in the diagram.
Figure 4-4 Finite-state diagram for example scanner.
There is a set of subprograms which many scanners employ to perform some of the more frequently required tasks. The function GET_CHAR, for example, returns the next input character from the source text. The function KEYWORD determines if its argument is a keyword and if so returns the internal representation number for this token. Other procedures may be used to add a new identifier to the symbol table.
By representing the scanner as a finite-state diagram, it can be easily implemented using a case statement or by simulating a case statement where each case represents one of the states attainable after a state transition from the starting state. The code for each case determines the token by using the longest sequence of input characters possible and performs any processing associated with this token. This may involve converting a constant to its internal numeric form or adding an identifier to the symbol table. Then the scanner returns the internal representation number of the token and possibly its location in some table. An algorithm based on the above observations follows.
Procedure SCAN(PROGRAM, LOOKAHEAD, CHAR, TOKEN, POS). This procedure is an implementation of the scanner specified by the finite-state machine in Fig. 4-4. Given the source string, PROGRAM, this algorithm returns the internal representation number of the next token, TOKEN, in that string. If this token represents an identifier, literal, or constant, then the procedure also returns its numeric table position, POS. CHAR represents the current character being scanned in the source string. LOOKAHEAD is a logical variable which designates whether or not the lookahead symbol in CHAR has been used in the previous call to SCAN. A value of "false" denotes that lookahead was not used. The following functions are used in the algorithm:
GET_CHAR(PROGRAM). Returns the next character in the source string. INSERT(STRING, type). Inserts the given token, STRING (if necessary), and its
type (i.e., a constant, literal, or variable name) into the symbol table. KEYWORD(STRING). Returns the internal representation number of its argument if it is a keyword and 0 otherwise.
The local variable STRING contains the actual token consisting of a variable name, literal, or constant. Finally, the variables DIVISION, LEQ, NEQ, LTN, GEQ, GTN, EQ, LEFT, RIGHT, ADDITION, SUBTRACTION, MULTIPLICATION, ASSIGNMENT, SEMICOLON, LITERAL, IDENTIFIER, and CONSTANT contain the internal representation numbers of the tokens![]()
![]() literals, identifiers, and constants, respectively. Note that the symbol □ denotes a blank.
literals, identifiers, and constants, respectively. Note that the symbol □ denotes a blank.
This procedure uses the parameters LOOKAHEAD and CHAR to describe what has happened in the scanning of the next input character in the previous invocation of the procedure. If LOOKAHEAD has the value of true, the next input character is already in CHAR. Step 1 initializes the value of POS to a default value of zero. POS is set to its appropriate table value for an identifier, constant, or literal in step 4. Step 2 obtains the current input symbol if lookahead was not used in the previous invocation of SCAN. Step 3 repeatedly performs step 4. Since comments and blanks are ignored in the scanning process, step 4 must be repeated in such cases. Step 4, although lengthy, is straightforward. The case statement selects, depending on the value of the current character scanned (given by CHAR), the particular algorithm segment to be performed and causes the appropriate transfer to a state that implements the finite-state acceptor described in Fig. 4-4. Note the placement of Return statements in this step. A trace of this procedure is left as an exercise.
The model of a scanner presented here returns to the parser both a token and its table location, if applicable. For certain block-structured languages, however, table operations would be done later in the compilation process. In such cases the scanner would only return a token to the parser.
In some languages, it is not always possible to determine what a token is at the point where it has been entirely read when using the model of a FSA. The classic example is illustrated by the following two FORTRAN examples:
DOIOI = 1, 20 DOIOI = 1 + 20
The first statement is the start of a loop, and DOIOI consists of the three tokens, DO, 10, and I while in the second statement, DOIOI is a valid FORTRAN identifier. It is impossible to tell after having readjust DO whether or not DO is part of an identifier or the token starting a DO statement. The problem can be solved using lookahead. Thus, whenever a special case arises where it is unclear as to what the token is, the scanner must look ahead in the source text in order to resolve this uncertainty.
Lookahead can be implemented using an input buffer. For example, parts of the source text are read several characters at a time into a vector. Two pointers are used. One pointer indicates the position of the current character being read in the buffer and the other pointer, the lookahead pointer, scans further along the input buffer whenever a decision must be made about a token. A buffering scheme must take into account the situation in which lookahead is required beyond the end of the current buffer and must be able to manage the input buffer to handle this situation.
Language policies must be taken into consideration when designing a scanner. Languages such as PL/I ignore blanks except for separating keywords and identifiers while other languages, such as FORTRAN, completely ignore blanks. Furthermore, keywords may or may not be reserved. The scanner presented in this section was designed assuming that keywords are reserved, but such is not the case in a language like PL/I. In such cases the scanner would return a token and let the parser decide whether or not a token was a keyword. As discussed earlier, table operations could be done later in the compilation process.
It was mentioned earlier that scanners can use regular grammars for recognizing tokens. Regular expressions can also be used to define a scanner, and the next section encompasses these two notions. Showing how regular expressions are used to define scanners, however, will be delayed until Sec. 4-7.