Run-Time Storage Organization and Management (Compiler Writing) Part 3

Management of Variable-Length Blocks

The situation becomes more complicated if the storage requests can be for blocks of varying sizes, as is common with variable-length strings or when the allocation of data structures of varying sizes is being explicitly controlled. We can no longer treat the available heap storage as a linked list of blocks of the correct size, for there is no correct size. Instead, our linked list can contain blocks of various sizes, each being a potential candidate for allocation or for subdivision into two blocks of smaller size—one subblock for immediate allocation and one for retention on the available list.

With variable-sized blocks, the problem of fragmentation is encountered. This is a problem which did not appear in the case of fixed-size requests. Two types of memory fragmentation can arise: external fragmentation and internal fragmentation. These are explained as follows.

If a large number of storage blocks are requested and later returned to heap storage, the linked list of available blocks can be reasonably lengthy (especially if returned contiguous blocks are not fused into one). This means that the average size of an available block becomes small and that there are probably very few blocks which are large. If a request for a large block is received, it may have to be refused because there is no single block on the availability list that is big enough even though the total amount of available storage may be much greater than the requested amount. This phenomenon of decomposing the total available storage into a large number of relatively small blocks is called external fragmentation.

We can attempt to inhibit external fragmentation somewhat by occasionally allocating a block that is larger than the requested size (i.e., by refusing to split a block into pieces, one of which might be quite small). If we do this, it could happen that a request for heap storage must be refused because of the lack of blocks of the required size. This can take place even though the amount of storage that is "wasted" (i.e., allocated but unused) is more than sufficient to satisfy the request. This phenomenon of partitioning the total unused storage into available blocks and allocating these blocks with some portion of the blocks remaining unused and unavailable is called internal fragmentation.

Any algorithm for heap storage management in a context where variable-sized blocks will be used must seek, in some way or another, to minimize the inefficiencies due to fragmentation. Fragmentation is the major factor in making these algorithms more complicated than those for fixed-size blocks. In addition, because the sizes of blocks cannot be known in advance, each block generally uses a SIZE field to record its current size as well as a LINK field to maintain the linked structure of the availability list. For convenience it is assumed that these fields are in the first word of each block or can be accessed directly once the address of the first word of the block is provided.

First-fit heap storage-management strategy. Assume the availability list has a list head of the form given in Fig. 9-12, with AVAIL being the address of this list head, LINK(AVAIL) being a pointer to the first block on the free list, and SIZE(AVAIL) being set to 0. Then one method for servicing a request for a block of size n can be formulated as follows.

Function ALLOCATE_FIRST (AVAIL, MIN, n). Given AVAIL, the address of the list head in heap storage and n, the size of block requested, this function returns P, the address of a block of length ^ n, with SIZE(P) set to the actual length of the block. The variable MIN records the amount of heap storage that is willing to be wasted in order to reduce external fragmentation. That is, no block of size MIN or smaller will be formed by splitting a particular block, k is a local variable which contains the difference between the size of a block and the requested block size. Q is also a local variable and points to the block previous to P in the linked list of available blocks.

This function assumes that arithmetic can be performed on addresses. If it is desired to eliminate internal fragmentation completely, simply set MIN to

0—though the utility of a block of size 1 is not very clear, especially since this single location (and perhaps, more!) is taken up by the SIZE and LINK fields.

The function just given is commonly called a first-fit algorithm because the block that is allocated is the first block (or a part) that is found to be larger than the requested amount. One might suspect that a best-fit algorithm might be preferable, but, in fact, this is not necessarily the case. The best-fit method does not use the first suitable block found but instead continues searching the list until the smallest suitable block has been found. This tends to save the larger blocks for times when they are needed to service large requests. However, the best-fit method does have the unfortunate tendency to produce a larger number of very small free blocks, and these are often unusable by almost all requests. Furthermore, the best-fit method requires a search of the entire availability list containing, say, N blocks, while the average length of search for the first-fit method would be N/2 or less, depending on the requested size.

The choice of methods, in any case, must be made in the context of some knowledge about the types of requests that will be encountered. Given a particular set of circumstances, the best-fit method might give better performance than the first-fit method, offsetting the potentially longer search time. It is interesting to note, however, that during the same series of simulations of storage-usage patterns performed in order to compare various management strategies, Knuth (1973) discovered that the first-fit method outperformed the best-fit method in all cases examined.

To this point, nothing has been said about any ordering imposed on the list of free blocks. This can have a significant effect on performance. If blocks on the availability list are ordered by size, the search time of the best-fit’ method can be reduced. An ascending-order sort has the effect of converting first fit to best fit. Descending order reduces the first fit’s search time to one because the first block found would be the largest. However, this can potentially convert first-fit into a method known as " worst-fit," in which the largest block is always used regardless of the size of the request. It may also cause unnecessary generation of many small blocks.

There is another ordering that might be imposed, however. This is to have the blocks on the availability list ordered by address (increasing, let us assume). This type of ordering does not necessarily improve search times for blocks of particular sizes, because there is no relation between block address and block size. However, it does make it possible to reduce external fragmentation, and it would tend to reduce all search times because the availability list can be shorter. Blocks sorted by address can be checked upon release, and if two consecutive blocks on the list are found to be contiguous, they are fused to form one larger block. This technique tends to keep block sizes larger and hence to keep the number of blocks smaller. More will be said on this fusing of blocks when algorithms are formulated for the release of allocated blocks. There is a lot of evidence, though, to suggest that, in the absence of special offsetting conditions, first-fit applied to an availability list ordered by address is a good method to adopt.

Another addition that can be made to the first-fit algorithm that can reduce ts search time quite noticeably is also described by Knuth. The modification lies in starting a search for a suitable block at the point where the previous search terminated rather than always with the first block. This tends to distribute smaller blocks evenly over the entire list, rather than having them concentrated near the front of the list. Knuth (1973) has shown through a series of simulations that this modification reduces the average length of search for the first-fit method to N/3 as opposed to N/2. Function ALLOCATE_FIRST_M is the first-fit algorithm modified to make use of this varying search start point.

Function ALLOCATE_FIRST_M (AVAIL, MIN, n, M). Given AVAIL, n, and MIN

as before, and M, a pointer to the last examined available block on the previous invocation of this routine, the function returns P, the address of a suitable block, and defines a new value for M. Prior to the first call to this routine, M is assumed to have been initialized to AVAIL. TIME is a flag associated with the traversal of the list. This flag is set to 1 when the end of the list is encountered, k is a local variable which contains the difference between the size of a block and the requested block size. Q is a local variable as well and points to the block previous to P in the linked list of available nodes.

Let us now consider the release of an allocated block of storage and its return to the free list. We still ignore the question of when and how the decision is made to free a block of storage and simply assume that a block of storage, starting at address RB, is now considered to be unused and a candidate for reallocation. It is also assumed that a size field, SIZE(RB), is located in the first word of the block and contains the actual size of the block being freed.

The simplest solution is to insert every freed block as a new first block on an unordered free list. This does, indeed, require a minimum of processing, but it has a serious drawback. After the heap storage manager has been operating for a while, the availability list is very likely to contain a large number of small blocks. The search time for the allocation routine will become longer and longer and there will be an ever-increasing risk of being unable to meet certain requests because all the blocks are simply too small. The problem is, of course, that in this simple freeing method no mechanism is running in opposition to the splitting mechanism in the allocation routine. In other words, big blocks are never recreated.

The obvious solution is to form one block out of two contiguous free blocks. If every newly released block is checked for contiguity with its predecessor and successor blocks on the availability list and merged with them whenever contiguity occurs, the availability list will always contain the smallest number of blocks. Each block is as large as possible given the current segments that are allocated. In order for this to work, however, the availability list must be kept in order by block address, and this then requires a search of the availability list in order to determine the position for insertion of a newly freed block.

The following algorithm can be used to insert a block on the availability list, merging it as necessary with contiguous neighbors. Since we have available a second pointer into the availability list—the variable search start point—we can make use of it as a starting point rather than AVAIL on some occasions. It can be shown that this reduces the average length of search from N/2 to N/3. The algorithm incorporates this modification.

Procedure FREE_BLOCK (AVAIL, RB, M). Given AVAIL, the address of the list head, M, the variable starting point for searching in the allocation routine, and RB, the address of the block to be inserted, this procedure inserts block RB into the availability list and merges contiguous blocks whenever possible. The algorithm assumes that AVAIL is less than the address of any block. This is guaranteed if the list head (with SIZE(AVAIL) set to 0) is the first word of the entire section of memory available for allocation. It is also assumed that the value NULL can be compared with valid addresses using any of the relational operators, with only # yielding a true result. Q is a pointer which denotes the predecessor of the node being freed.

1. [Initialize to either beginning or variable search point]

 

 

To summarize, we now have a heap storage-allocation method with an average search time that can be very short, and we have a heap storage-freeing method with an average search time of about N/3. Our release technique tends to reduce external fragmentation because it maintains block sizes as large as possible. The degree of internal fragmentation is under our control through the variable MIN, though there is a trade-off between internal fragmentation and both external fragmentation and search times. Yet looking at these two heap storage-management mechanisms in terms of search times, we can see that the deallocation routine is a potential bottleneck because of the N/3 average length of search. It is appropriate, therefore, to consider a deallocation routine which does not require this length of searching time. The " boundary-tag" method of Knuth is the strategy chosen.

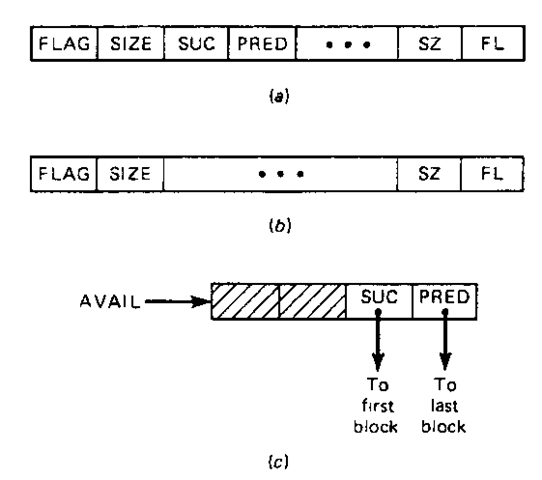
Boundary-tag heap storage-management strategy. In the storage-release procedure just given, it is the search through the blocks in the sorted list which allows the determination of the predecessor and successor blocks. Having these, it is simple to determine if they and the released block are contiguous. Without the search, all that one can do is examine the two words that are the immediate predecessor and successor of the released block. But unless they are specially marked with flags, there is no immediate way of telling whether or not the predecessor and successor blocks are on the availability list. Consequently, in the boundary-tag method the first and last words of blocks are made to contain a flag field which indicates whether or not the block is allocated. It is also useful to have the last word of a block also contain a size field. From the last word of a block, the address of the first word can be determined directly. And finally, since searching is being avoided, the availability list is maintained as a doubly linked list. The price paid for eliminating searching is therefore more storage taken up for control fields.

This may not be worthwhile if, depending on the frequency and the nature of the deallocations, the availability list tends to be fairly short or the average block size is small. In other cases, it may be a very useful way of speeding up the deallocation of storage.

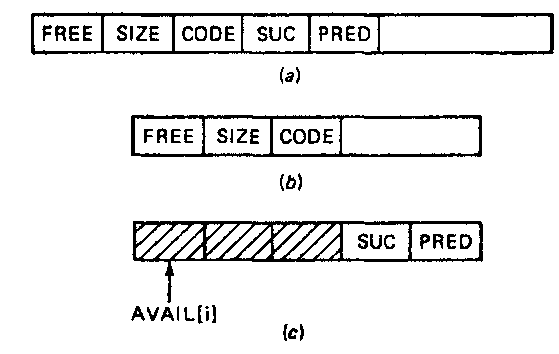
The storage representation of the blocks is of the form given in Fig. 9-13a and b when the blocks are on the availability list and allocated, respectively. If the block starting at address P is free, the FLAG and FL fields are set to 0; otherwise these fields are set to a positive value for a block which is allocated. The fields SIZE and SZ contain the length of block P. SUC(P) and PRED(P) are pointers to the successor and predecessor, respectively, of block P on the availability list. A list head is also assumed of the form given in Fig. 9-13c, with AVAIL being its address. The list head is considered to be the successor and the predecessor of the last and first blocks on the availability list. For convenience, we assume that the list head is outside the segment of storage that is to be managed and that the first and last words of this segment have the correct flags set to show that these two words have been allocated. We now proceed to formulate a deallocation algorithm based on this representation.

Procedure FREE_BOUNDARY_TAG (RB, M). Given the block structure just described, this procedure inserts a block with address RB onto the availability list, merging it with contiguous blocks as necessary. It also redefines M, the variable search start point, if required. It is assumed that having the address of the first word of the block is sufficient to access immediately the FLAG, SIZE, SUC, and PR ED fields, and that the address of the last word of the block gives direct access to the SZ and FL fields. The algorithm itself basically performs an insertion into a two-way linked list. Q is a local variable which points to various blocks during the process of merging.

Figure 9-13 Boundary-tag block structure. (a) Free block. (b) Allocated block, (c) List head block.

 

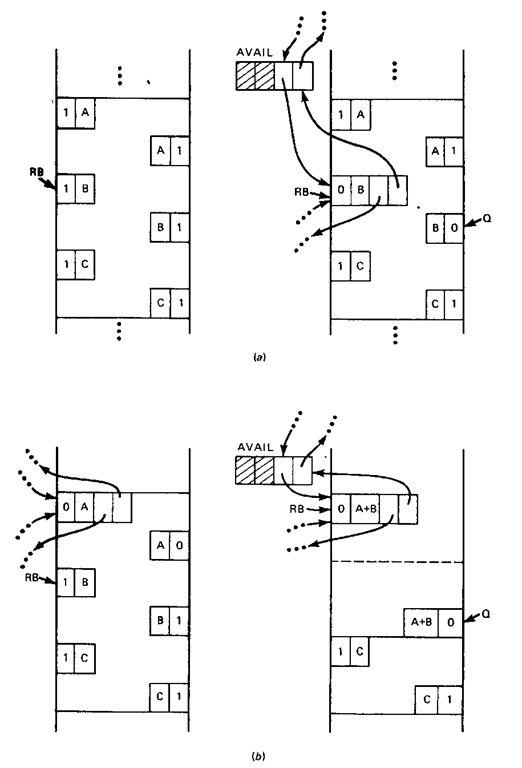
In performing the deallocation, four possible cases arise in Procedure FREE_BOUNDARY_TAG, and these are exhibited in Fig. 9-14. In the first case, as shown in Fig. 9-14a, the freed block pointed to by RB is of size B and has no immediate neighbors that are already marked as free. That is, both the block with a size field of A and the block with the size field of C are already allocated and hence their flag fields are marked with a 1. In this case, neither step 1 or 2 of the algorithm is applied, and with the application of step 3 the freed block is simply placed at the front of the availability Hst as depicted in the right-hand side of Fig. 9-14a.

The second case is shown in Fig. 9-146. The neighbor block of size A is shown to be on the availability list. In this case, step 1 of the algorithm collapses the block pointed to by RB and its neighbor of size A to a new block of size A + B. Note that in collapsing the blocks the block of size A is removed from the availability list. Step 2 is not applied in this case and step 3 simply inserts the new collapsed block at the front of the availability list.

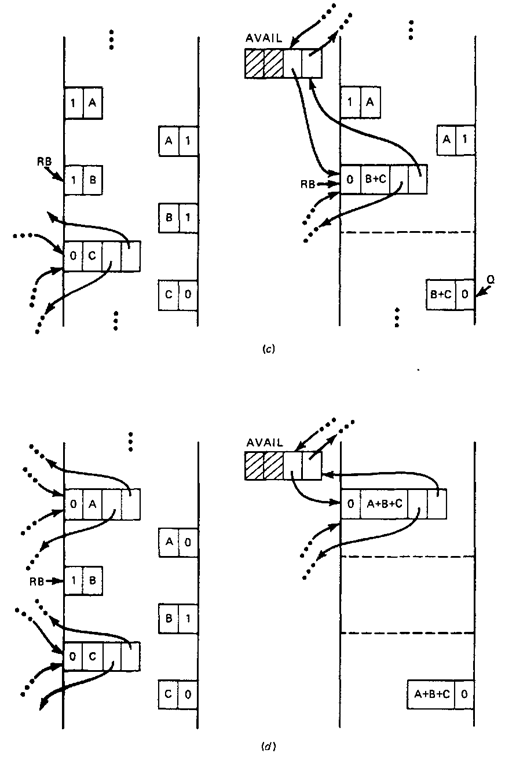
The third case shows the situation in which the freed block is collapsed with a neighbor that succeeds it in heap storage. The condition in step 1 is not met; however, the condition in step 2 is true.

Figure 9-14 An illustration of the four cases of block deallocation in the boundary-tag method.

The freed block is collapsed with the block of length C, and the block of length C is removed from the free list. The final step places the collapsed block at the head of the availability list.

The fourth case combines the effects of cases 2 and 3 discussed previously. Both neighbor blocks are collapsed in steps 1 and 2, and the large collapsed block is again inserted as the first block in the availability list.

Buddy-system heap storage-management strategy. Up to this point the sizes of blocks have either been fixed or completely arbitrary (though larger than some minimum value). Another technique used in heap storage management is to restrict the sizes of blocks to some fixed set of sizes. All the blocks of each size can be linked together with the intent of speeding up the search for a block of suitable size. For a request for a block of size n, the number m, the smallest of the fixed sizes equal to or larger than n, is determined, and a block of size m is allocated. If no block of size m is available, a larger block is split into two subblocks (known as "buddies"), each also of fixed size, and this process is repeated until a block of size m is produced.

Besides the improvement in search time, there is another advantage in using this technique. The collapsing of two smaller blocks into one larger block is relatively easy, since only the two buddies formed by splitting a larger block may be combined to form this larger block once again. Because the sizes are fixed relative to one another, the address of the buddy of a block is relatively easily determined.

There are, however, some potential disadvantages associated with this technique. Internal fragmentation will be increased generally, because of the allocation of blocks which may be somewhat larger than the requested size. As well, there can be an increased amount of external fragmentation due to the fact that two blocks may be contiguous and yet not merged because they are not buddies. Generally, though, this technique of storage management has proved to be quite efficient with performance comparable with the previous methods discussed.

The usual approach in implementing this method of storage management is to specify the fixed sizes, F0, F1…..^max> f°r blocks according to some pattern such as the recurrence relation

where a, b,… ,c are minimum block sizes that are used, and where k = 1 or 2 or 3 or… . For example, if A: is 1 and F0 is 1, the block sizes, which are 1,2,4,8,16,…, are the successive powers of 2 and the method is called the "binary buddy system." If k = 2 with F0 = Fl = 1, the sizes are just the successive members of the Fibonacci sequence 1,1,2, 3,5,8,13,… . In all likelihood, though, the F0, Fv etc.. terms are not defined to be such small values. Blocks of size 1 are not of much use, especially if they must also carry control information so that the allocation and release mechanisms will work.

The feature that makes this system work is that the merges must correspond exactly to the splits. By this we mean that the only two blocks that can be merged are precisely the two that were formed by splitting. Furthermore, before each block can be reformed, each of its subblocks must be reformed from their subblocks. Consequently, the storage block pattern formed by the sequence of splits has the form of a binary tree. The problem that is faced is the recording of the position of a particular block within this tree structure. A rather elegant solution has been provided by Hinds (1975) in a storage-management application.

His solution consists of a coding for each block in such a way that the splitting sequence which produced that block can be reconstructed. Looking at the recurrence relationif we specify that the F„_l term corresponds to the block that forms the left branch of a split (assumed to be at the lower address) and the Fn_k term is the right branch, then all that must be recorded for each block is the size of the block, the number of splits it took to form the block, and whether it is a left block or a right block. Since one left block and one right block are formed in each split, we need only record the count of left blocks. In fact, this allows us to code the left-or-right factor together with the split count in one coded field. The left block has the relative split count (a number greater than 0) while the right block has a code of 0. The code for the parent block is thus determined in relation to the left block. The formulas to use are the following:

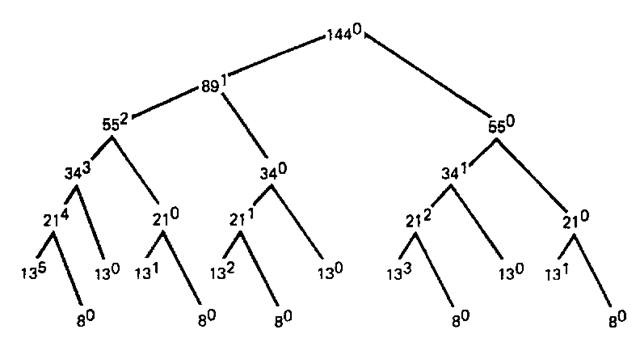
As an example, consider a storage block of 144 cells and the recurrence relation

The entire tree of possible splits is given in Fig. 9-15, where the vertex value is the block size and the superscript is the code value as computed by the previous formulas.

Consider the tree cross section which is the set of potential blocks of size 13. A block of size 13 with code of 0 is the right block formed by splitting a block of size 34. The left or right nature of this size 34 block is determined by the left buddy for the block of size 13. If its left buddy (of size 21) has a code of 1, the size 34 block is a right block for some larger block of size 89, while if the left buddy has a code greater than 1, the block of size 34 is a left block of some still larger block. A block of size 13 with a code value greater than 0 is the left block of a split block of size 21. The numeric value of the code for a left block of size 13 is the number of splits of some higher right block that had to be made to get this

Figure 9-15 Storage-management tree.

left block of size 13. Or, in other words, the value of the code for a left block is the number of merges that this left block must undergo to become the first 13 locations of some larger block which is finally a right block.

For the algorithms to be presented, it will be assumed that blocks are of the structure given in Fig. 9-16a and b, which correspond to free and allocated blocks, respectively. FREE(P) is 0 or greater than 0 depending on whether block P is free or not, SIZE(P) contains the value i for block P of size Fn and SUC(P) and PRED(P) are the forward and backward pointers to other free blocks of size Ft in a doubly linked list of all the free blocks of size Fr The list head with address AVAIL[i] for this list is given in Fig. 9-16e. CODE(P) for block P is the code giving the left- or right-handedness of block P and the relative split count, if P is a left block. In addition to the array of list heads AVAIL[0:MAX], we also have the array F[0:MAX] which records the block sizes /■), 0 < i <, MAX, as determined by the recurrence relation. It is assumed that F0 has a value large enough to allow the storage of all the control fields.

The following are two subalgorithms which take care of the insertion and deletion of blocks into and from the above linked lists.

Procedure 1NSERT(P, i). Given the arrays and block structures as previously described and parameters i and P (address of a block of size Ft), this procedure inserts P into the list headed by AVAIL[i].

 

 

 

Figure 9-16 Buddy-system block structure. (a) Free block, (b) Allocated block, (c) List head block.

Procedure DELETE(P). Given the arrays and block structures as previously described and parameter P (the address of a block), this procedure deletes block P from the list in which it appears.

The following algorithms service the requests for storage blocks and the deallocation of blocks in heap storage. Both presume that the value of k has been fixed so as to determine which recurrence relation is being used.

Function ALLOCATE_BUDDY (n). Given the arrays and block structures as previously described, this function receives a request for a block of size n and returns the pointer P set to the address of a block of size Ft which is the smallest size larger than or equal to n. It is assumed that the value of k has been fixed so as to determine which recurrence relation is being used. Local variables include i and j (integers) and Q (pointer).

 

 

Procedure FREE_BUDDY (P). Given a block beginning at address P as well as the block structure and arrays described previously, this procedure inserts P (or the mergers of it with appropriate buddies) onto the proper free list. It is assumed that the value of k has been fixed so. as to determine which recurrence relation is being used. Q is a local pointer variable.

It should be noted that when k = 1 (when the strategy is the binary buddy system) the addresses of buddies differ from each other by amounts that are integral powers of 2. Since all addresses are in binary representation in a computer, the address calculation given above can be replaced by a method that makes use of this fact, thus possibly speeding up these algorithms.

With regard to the performance of these algorithms, Knuth’s simulations showed that the buddy system performed quite well, comparable with his boundary-tag method, and, in fact, the buddy system has proven itself in practice. Statistical analysis has been performed on the Fibonacci system, and the results show it to be superior to the binary buddy system. The advantage of the Fibonacci buddy system is that the average amount of wasted storage is less than for the binary buddy system. A wider range of block sizes is available in the Fibonacci system because, for a given integer, there are at least as many Fibonacci numbers as there are integral powers of 2. Hence more block sizes are available and, therefore, it is more likely that a fit between the requested amount and the allocated amount is possible. One can conclude, however, that both storage-allocation methods are suitable candidates for a storage-management system.

Thus far in the section we have surveyed a number of heap storage-allocation strategies. Yet to be fully considered, however, is the question of when and how a decision to free storage is made.

The question of when to free static and dynamic storage is easily answered. As we have seen earlier in this topic, static storage is freed when the execution of a program is completed and dynamic storage is released upon termination of a block.

With explicitly controlled heap storage-allocation strategies (such as that adopted using PL/I’s ALLOCATE and FREE statements on based storage), the explicit use of free staterr its should dictate exactly when storage can be released. However, the blind ad ption of such a strategy can lead to disastrous results through the creation of dangling references. Consider, for example, the following sequence of PL/I instructions:

First, a copy of NODE is created. The address of this created variable is copied into the base-pointer variable P. Next, the pointer variable Q is set to point to the copy of NODE allocated p’ eviously. Finally, the copy of NODE is released, the base pointer P is set to -ULL but the value of Q remains unchanged and pointing to a released block of storage. Obviously some difficult-to-detect errors can arise when programmers are given such a direct control over the relinquishing of heap storage.

To circumvent this problem, and to protect programmers from themselves, most language implementors reserve the task of heap storage release for the heap manager, even if the language provides a free command that the programmer can use. The problem that then arises is one of determining when storage can actually be freed. Two main methods can be used, and these are described in the next two subsections.