1. Introduction
Complex software systems integrating sophisticated machine learning techniques have been developed to elucidate the structures and functions of genes, but accurate gene annotation is still difficult to achieve, primarily due to the complexity inherent in biological systems. If the biological signals surrounding coding exons could be detected perfectly, then the protein-coding regions of all genes could be identified simply by removing the introns, concatenating all the exons, and reading off the protein sequence from start to stop. Not surprisingly, most successful gene-finding algorithms integrate signal sensors that are intended to identify the usually short sequence patterns in the genomic DNA that correspond directly to regions on mRNA or pre-mRNA that have an important role in splicing or translation. Unfortunately, DNA sequence signals have low information content and are very hard to distinguish from nonfunctional patterns, making signal detection a challenging classification problem.
This review provides mainly background information about signal prediction in the gene-finding framework from a computational perspective, without giving too many biological details (for which the interested reader is invited to look at the cited papers). It starts by presenting the most frequently predicted biological signals and ends with a general overview of the most widely used methods in signal detection.
2. Commonly predicted biological signals
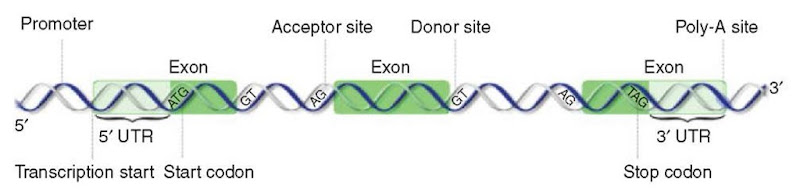
The signals that are usually modeled by gene-finding packages are transcription promoter elements, translational start and stop codons, splice sites, and polyadeny-lation sites, but computational methods have been designed for many other signals, including branch points, ribosome-binding sites, transcription terminators, exon enhancers, and various transcription factor binding sites. In this section, we present some of the biological signals that are most often addressed by signal recognition programs. These signals are shown in Figure 1 in rapport to the structure of a gene.
Figure 1 Important biological signals usually modeled by gene finders
2.1. Splice sites
Splice sites are one class of signals that determine the boundaries between exons and introns. The biological rules that govern splice site selection are not completely understood (Reed, 2000). It is well known, though, that recognition of the splicing signals in pre-mRNA is carried out by a complex of proteins and small nuclear RNAs known collectively as the spliceosome, which splices out the introns and produces the mature mRNA transcript. The components of the spliceosome are, in general, highly conserved among eukaryotes (Mount and Salz, 2000), but the splice site consensus sequences are short and degenerate. Usually, the 5′ boundary or donor site of introns in most eukaryotes contains the dinucleotide GT (GU in pre-mRNA), while the 3′ boundary or acceptor site contains the dinucleotide AG. In addition to these dimers, a pyrimidine-rich region precedes the AG at the acceptor site, a shorter consensus follows the GT at the donor site, and a very weak consensus sequence appears at the branch point, approximately 30 nucleotides (nt) upstream from the acceptor site.
A number of computational methods have been developed to identify splice sites. Some are stand-alone splice site finders (see for instance Hebsgaard et al., 1996; Reese et al., 1997; Brendel and Kleffe, 1998; Pertea et al., 2001 for a few examples), but often gene finders identify splice sites as a subroutine, and their performance is greatly influenced by the quality of these splice sensors.
2.2. Translational start and stop codons
Since translational start and stop codons, together with the splice sites, determine the complete coding portion of a gene, their recognition is crucial to the success of computational gene-finding strategies. Unfortunately, patterns in the vicinity of the translational start and stop sites are even less distinctive than those around the splice sites. While the translational stop is almost always identified by the first in-frame stop codon, computational recognition of the start codon proves to be a difficult task in gene finding. Shine-Dalgarno (Shine and Dalgarno, 1974) and Kozak sequences (Kozak, 2001) describe consensus motifs in the context of the translation initiation both in bacteria and in eukaryotes. However, these consensus patterns have very limited power in discriminating the true start codons from other potential starts in a DNA sequence. The lack of strong identifying signals means that start signal recognition usually has very high false-positive rates, even higher than in the case of splice site detection (Salzberg, 1997; Pertea and Salzberg, 2002).
2.3. Promoters and transcription start sites
Finding the DNA site to which RNA polymerase will bind and initiate transcription is such a complicated task that most gene finders do not even attempt to integrate it into the prediction model. A gene recognition program will usually predict only the protein coding region of the gene, from start to stop codon, leaving the untranslated exons and exon segments to be discovered by other methods. These methods frequently focus on the discovery of the transcription start site (TSS) of a gene, by trying to identify the promoter region, which is usually located adjacent to the TSS.
The promoter region typically extends 150-300 bp upstream from the transcription start site (in prokaryotes), and contains binding sites for RNA polymerase and a number of proteins that regulate the rate of transcription of the adjacent gene. Most bacterial promoters contain the consensus sequences TATAAT and TTGACA at around 10bp and 35bp respectively upstream of the TSS (Galas et al., 1985). Much less is known about eukaryote promoters. Most computational methods try to recognize the Goldberg-Hogness or TATA box that is centered around 25 bp upstream of the TSS and has the consensus sequence TATAAAA. A CAAT box and a GC-rich element have also been identified in several promoters (Bucher, 1990). Although many promoter and TSS prediction programs have been developed, their performance is less than satisfactory, due to the large numbers of false-positives that are generated (see for instance Fickett and Hatzigeorgiou, 1997; Ohler and Niemann, 2001 for an assessment of recent promoter recognition programs).
2.4. Transcription terminators and polyadenylation sites
At the end of the coding sequences, a signal called the transcription terminator causes the RNA polymerase to slow down and fall off the nascent transcript. It is composed of a sequence that is rich in the bases G and C, and can form a hairpin loop. Prediction of transcription terminators has been achieved with some success in bacterial genomes. Specificity in the 89-98% range was obtained by TransTerm (Ermolaeva etal., 2000), which identifies terminators by searching for a hairpin structure in proximity of a downstream U-rich region.
As transcription is nearly completed, a polyadenylation signal where the mRNA is cut is encountered. A polyadenylic acid sequence of varying length is then added posttranscriptionally to the primary transcript as part of the nuclear processing of RNA. This poly-A tail is thought to help transport the mRNA out of the nucleus, and may stabilize the mRNA against degradation in the cytoplasm. Prediction of the location of the poly-A signal is included in many gene-recognition programs, since careful determination of the gene’s ends plays an important role in determining the accuracy of the programs. When the end of a gene is not correctly predicted, it tends to be either truncated or fused with the next gene by the gene finder. Poly-A signal prediction has been also considered by stand-alone programs (Salamov and Solovyev, 1997; Tabaska and Zhang, 1999) that can predict the well-known AAUAAA signal as well as other poly-A sites.
3. Computational methods for signal prediction
In this section, we describe several of the most popular methods for signal detection in DNA sequences, but many others have appeared over the years. These methods range from very simple ones, such as computation of consensus sequences and position weight matrices, to more complex computational methods such as neural networks, Markov models, and decision trees. In general, the best current methods combine many different types of evidence (Salzberg et al., 1998), using nucleotides in a relatively wide window around the core sequence pattern. Because all of these methods are essentially statistical, they have become more effective recently, due not to changes in the algorithms but rather to significant increases in the amount of genomic sequence data available.
3.1. Consensus analysis
Consensus sequence methods use a multiple alignment of functionally related sequences to identify the consensus, defined as a composite subsequence created using the most common base at each position in the multiple alignment. New sites are identified simply by matching them to the consensus sequence. The match can be exact or it can be within a neighborhood consisting of all subsequences within a fixed distance k from the consensus sequence, where the most common distance used between two sequences of the same length is the Hamming distance. These techniques have been used to characterize a variety of different biological signals; for example, the consensus (A,C)AG/GU(A,G)AGU with mismatches was described at the 5′ end of introns back in 1990 (Senapathy et al., 1990). Different programs implement this technique either by itself or combined with other methods to predict functional sites (e.g., SpliceView (Rogozin and Milanesi, 1997) or SplicePredictor (Brendel and Kleffe, 1998)).
3.2. Weight matrices
The weight matrix model (WMM) summarizes the consensus sequence information by specifying the probabilities of each of the four nucleotides in each position of the DNA sequence (Stormo, 1990; Gelfand, 1995). Values in the weight matrix are determined by aligning known sequences for a given signal type, and computing the fraction of each residue at each position. Formally, if the signal pattern is I nucleotides in length, then the probability that the sequence X = x\x2 …xi is a signal of that type is given by p(X) = Y\i=l p(l)(xi), where p(l)(xi) is the probability of generating nucleotide xl at position i of the signal. Fickett (1996) describes a common variation of the above technique, the position weight matrix, which uses the relative frequency of each base in each position by replacing p(i)(xi) with p(l) (xi)/p(xi), where p(xi) is the probability of generating nucleotide xi independent of its position in the signal. An important limitation of the weight matrices is the underlying simplifying assumption of independence between positions. A modified form of the WMM known as “inhomogeneous Markov model” or “weight array model” (IMM/WAM) has been introduced to capture nonindependence between positions (Zhang and Marr, 1993). Most commonly used is the first-order WAM in which the distribution at position i depends on the residue at position i – 1, but higher-order WAMs have been also described. While such higher-order models might succeed in reducing the high false-positive rates, they require the estimation of a very large number of parameters, thus an increased amount of training data, which is often not available. To reduce the problem of sample-size limitation, Burge and Karlin (1997) implement a generalization of the WAM, called “windowed weight array model” (WWAM), to detect splice site signals. In this method, the transition probabilities at a given position i are estimated by averaging the conditional probabilities observed at position i with those observed in a neighboring window of positions centered at position i. For instance, a second-order WWAM will estimate the transition probabilities for positions i from the data at positions i – 2, i – 1,l,l + 1, and i + 2, the underlying assumption here being that nearby positions have similar triplet biases.
3.3. Decision trees
A decision tree is a supervised learning method that learns to classify objects from a set of examples (where an “object” can be a DNA sequence or partial sequence). It takes the form of a tree structure of nodes and edges in which the root and the internal nodes test on one of the objects’ attributes. Each edge extending from an internal node of the tree represents one of the possible alternatives or courses of action available at that point. Depending on the outcome of the test, different paths in the tree are followed down to the tree’s leaves, which carry the names of classes into which the objects are placed. Most decision tree learning systems use an information-theoretic approach that minimizes the number of tests to classify an object. A typical approach is to use an information-based heuristic that selects the attribute providing the highest information gain (Quinlan, 1986), that is, the attribute that minimizes the information needed in the resulting subtrees to classify the elements. Formally, the information gain uses I = J] (pi ln pi), where pi is the probability that an object is in class i, as evaluation function for measuring the information of the initial set and the subsets produced after splitting. There have been many other approaches based on different evaluation functions, including the Gini index, chi-square tests, and other metrics (Murthy et al., 1994).
Decision tree-based classification methods have applications in a wide variety of domains, including DNA sequence analysis. SpliceProximalCheck (Thanaraj and Robinson, 2000), for example, is a program that uses a decision tree to discriminate true splice sites from false ones that may be located physically close to real ones.
An interesting application of decision trees was introduced by (Burge and Karlin (1997) to model complex dependencies in signals. Their approach, called maximal dependence decomposition (MDD), tries to capture the most significant adjacent and nonadjacent dependencies in a signal using an iterative subdivision of the training data. MDD trees are constructed from a set D of N aligned DNA sequences of length k , extracted from a set of signal sites. For each of the k positions, let the most frequent base at that position be the consensus base. The variable C i will be 1 if the nucleotide at position i matches the consensus at position i, 0 otherwise. Next, compute the x2 statistics between the variables Ci and Xj (which identifies the nucleotide at position j ), for each i, j pair with i = j . If strong dependencies are detected, then proceed as in Burge and Karlin (1997) by partitioning the data into two subsets based on those positions. Recursive application of this procedure builds a small tree. Each leaf of this tree contains a subset of the signal sites used for training.
3.4. Markov models
Markov models have been in use for decades as a way of modeling sequences of events, and they translate very naturally to DNA sequence data. To score a sequence using a Markov chain, a gene finder needs to compute a set of probabilities from training data. These probabilities take the form P(bi\bi-\, bi-2,… ), where bi indicates the base in position i of the DNA sequence. Models that use Markov chains rely on the Markov assumption, which states that any event x is dependent only on a fixed number of prior events. Clearly, this assumption is not true for all DNA sequences, and the extent to which the Markov assumption is false defines a limitation on the model. Markov chains combined with the MDD method are implemented by the splice site predictor program GeneSplicer (Pertea et al., 2001).
Many gene finders such as Genscan (Burge and Karlin, 1997) or GeneMark. HMM (Lukashin and Borodovsky, 1998) model signals (e.g., promoters, poly-A sites, and different enhancers) by using hidden Markov models (HMMs) or their extended form, generalized hidden Markov models (GHMMs). HMMs are Markov chains in which the states are not directly observable, and only the output of a state is observable. HMMs are generally far more complex than Markov chains, because the model need not be a chain; rather, it can contain elaborate loops and branching structures. The output from (or input to) each state is a symbol (or a string of symbols in the case of GHMMs) from a finite set of symbols and is chosen randomly according to some probability distribution over the alphabet of the output symbols. The parameters of the HMM are estimated using an algorithm called the Expectation Maximization (E-M) algorithm, and the most probable interpretation of a DNA sequence is then found with the Viterbi algorithm (Eddy, 1996).
3.5. Neural networks
Neural networks (NNs) are a powerful tool for pattern classification. Some NNs are models of biological neural networks while others are not, but historically, much of the inspiration for the field of NNs came from the desire to produce artificial systems capable of sophisticated computations similar to those that the human brain routinely performs. There is no room here to review the extensive and complex literature on neural nets, but generally speaking, NNs are networks of many simple processors, each possibly having a small amount of local memory. These networks are usually connected in a layered, feed-forward architecture and have some sort of training rule whereby the weights of connections are adjusted on the basis of data.
Many types of biological signals have been predicted using NNs, including the following: Promoter 2.0 (Knudsen, 1999) and NNPP (Reese, 2001) for promoter prediction, NNSPLICE (Reese et al., 1997) and NetGene2 (Hebsgaard et al., 1996) for splice site recognition, and NetStart (Pedersen and Nielsen, 1997) for start codon determination.
3.6. Linear and quadratic discriminant analysis
In linear discriminate analysis (LDA), the examples to be classified are represented as points in an n-dimensional space defined by features, each of which represents a measurement of some property of the input. The main purpose of LDA is to predict class membership on the basis of a linear combination of the scores of individual features. This can be represented as a multidimensional hyper-plane (a decision surface) whose coefficients are determined by minimizing the prediction error using positive and negative training data sets. In the field of signal detection, LDA is implemented, for instance, in PromH (Solovyev and Shahmuradov, 2003), a promoter prediction program that uses linear discriminant functions that take into account conserved features and nucleotide sequences of promoter regions in pairs of orthologous genes. Quadratic discriminant analysis (QDA) generalizes LDA by finding an optimal quadratic surface instead. The promoter prediction program CorePromoter (Zhang, 1998) uses QDA computed from 5-tuples in the input DNA sequence to predict promoters.
4. Conclusions and future challenges
The accuracy of gene-recognition programs is relatively high (around 90% sensitivity and specificity) when computed merely on the basis of the number of correctly predicted coding nucleotides, but decreases significantly when considering the number of exons or genes predicted correctly. Determining the exact boundaries of a gene’s structural elements is highly influenced by the ability to predict correctly the signals surrounding the DNA coding regions.
Prediction of very small exons or shifted open-reading frames could benefit from better recognition of splicing regulatory patterns. Computational determination of alternative splicing of genes can also benefit from a better understanding of the rules that govern splice site selection (Black, 2000). Alternative splicing appears to be most common in vertebrates (e.g., at least 35% of the genes in the human genome have been shown to be alternatively spliced (Croft et al., 2000)), but other metazoan organisms and plants also experience a significant number of alternatively spliced genes (Brown and Simpson, 1998), a phenomenon that raises serious challenges for the current software programs for gene recognition. A dominant role in the regulation of alternative splicing is played by exon splicing enhancers (ESEs), which activate nearby splice sites and promote inclusion of exons in which they reside. ESEs have only recently begun to be included in computational models (Fairbrother et al., 2002; Cartegni et al., 2003).
Signals upstream and downstream of genes also have an important role in determining the exact locations of genes. Using currently available methods, it is easier to find the 3′ end of a gene than the 5′ end. More effort needs to be devoted to improving detection of the patterns preceding genes. Numerous TSS and promoter databases (Zhu and Zhang, 1999; Hershberg et al., 2001; Shahmuradov et al., 2003; Schmid et al., 2004; Suzuki et al., 2004) have been constructed (though their reliability is highly variable), which can help with the determination of the 5′ end of the genes in various organisms. As more complete genomic sequences and extensive experimental data become available, systematic computational and experimental approaches can be further exploited to increase our ability to find genes and regulatory signals in all organisms.