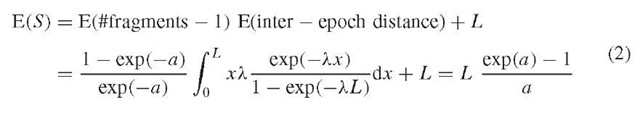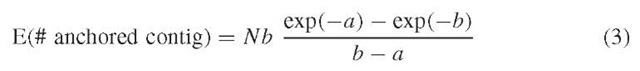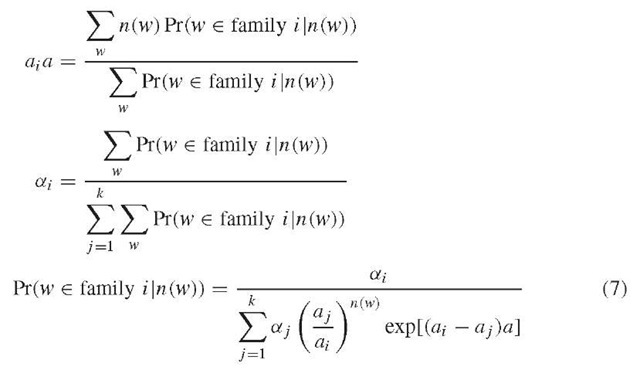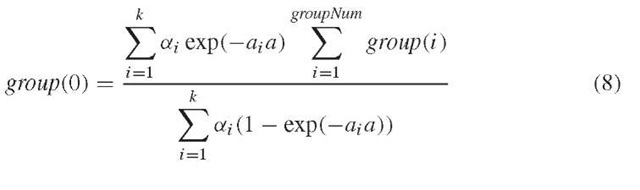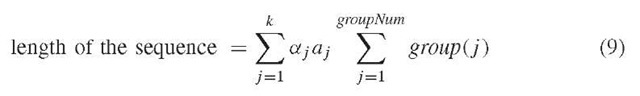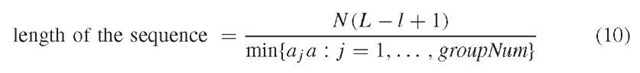1. Introduction
Sequencing of entire genomes of various organisms has become one of the basic tools of biology. However, quality of genome assembly depends to a large extent on the structure of genomic sequences, notably, signals such as repeats, polymorphisms, and nucleotide asymmetry as well as structural motifs such as protein motifs (see Article 28, Computational motif discovery, Volume 7), gene promoters, enhancers and suppressors (see Article 19, Promoter prediction, Volume 7 and Article 24, Exonic splicing enhancers and exonic splicing silencers, Volume 7), transcription factor binding sites, exon/intron splice junctions, regions of homology between sequences (see Article 39, IMPALA/RPS-BLAST/PSI-BLAST in protein sequence analysis, Volume 7), and protein docking sites. Probabilistic and statistical properties of the structural motifs are covered elsewhere in this volume (see Article 6, Statistical signals, Volume 7). We focus here on global features of genome assembly. The importance of these has been recognized in the topic by Waterman (1995), in seminal papers of Lander and Waterman (1988) and Li and Waterman (2003), as well as in the topic by Ewens and Grant (2001). Genome assembly can be modeled as a binomial/Poisson stochastic process. From the properties of this process, it is possible to derive the statistics of contig size and in this way to determine the coverage needed to achieve an assembly of desired quality. Analogously, probing the fragments with l-mers, it is possible to estimate the size of the genomic sequence, even when repeats are involved. This is accomplished by reconstructing the repeat structure, using an expectation-maximization algorithm. In the framework of this theory, it is also possible to estimate the total gap length and the stringency ratio.
In this review, we provide an account of these topics as well as of some other more specialized sequence signals such as polymorphisms, nucleotide asymmetry, and annotation by words. We also consider some real-life and made-up examples.
2. Statistics of genome assembly – contigs and anchors
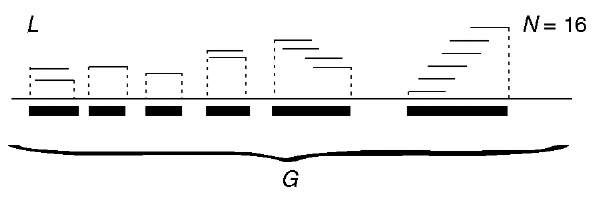
The following account is mainly based on Ewens and Grant (2001), Chapter 5. If biological details are omitted, shotgun genome sequencing can be reduced to assembly of a sequence of total length G, from N fragments (also called reads) of equal length L. Fragments are randomly selected from sequence G, and the assembly is feasible if there exists enough overlap between the fragments. To ensure this, the coverage a = NL/G should be large enough and certainly greater than 1. Depending on the strategy used, G may represent the entire genome (WGS, whole genome shotgun) or a subset of the genome. In Figure 1, we depict an example, this one with incomplete coverage.
A model for the random fragments is the binomial/Poisson stochastic point process, in which the coordinates of the left ends of the fragments are independent random variables uniformly distributed over G. Neglecting boundary effects, we obtain that the probability that the number of fragments with left ends in the interval (x, x -h) is equal to k and has distribution binomial (N, h/G) or approximately Poisson (Nh/G). A union of overlapping fragments is named a contig. In order to obtain a good quality of assembly, it is necessary that the contigs cover as much of G as possible. Mean number of contigs is equal to
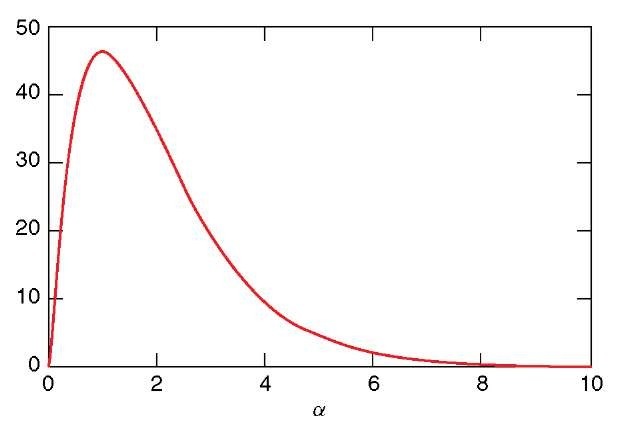
Figure 2 depicts E ( #contigs ) as a function of coverage a. E ( #contigs ) first increases but then decreases back, since smaller contigs coalesce with increasing coverage. A single (length G) contig is expected when coverage reaches a « 8. Expected contig size can be expressed as
E (S) increases as smaller contigs coalesce. For the data as in Figure 2, E (S) = G is expected when coverage reaches a « 8.
We might require that the contigs be anchored, that is, each of them include at least one anchor, which is a genomic site of known location (an element of a
Figure 1 Schematic depiction of 6 contigs assembled from N = 16 fragments, of length L each, of genomic sequence of length G
Figure 2 Expected number of contigs as a function of coverage a. Parameter values, L = 800, G = 100 000
gene map). Let us define the coverage with M anchors as equal to b = ML/G and suppose that the anchors follow the binomial/Poisson process. Then, we have
which is reduced to the nonanchored case as b ^-<x>, but usually is smaller. 3. Gap statistics
In a recent paper, Wendl and Yang (2004) discuss prediction of the size of gaps in WGS projects. According to the Lander and Waterman (1988) theory, the expected number of gaps is equal to
where a = (L – T)/G is the effective fractional read (fragment) length, with T being the minimum overlap required. Maximum gaps number consequently is equal to
Lander and Waterman (1988) theory also implies that stringency a, that is, the proportion of existing gaps to the expected maximum, can be expressed by the effective coverage 8 = N(L – T)/G, as a = E/Emax = 8 exp(1 – 8). Wendl and Yang (2004) proceed to demonstrate that these expressions underestimate stringency (as it was claimed earlier on) and provide semiempirical estimates of stringency, given coverage, aemp = 1.187 exp(-0.3348) for eukaryotes and aemp = 0.701 exp(-0.2118) for prokaryotes. These estimates were obtained by applying linear regression to log-linearized data from 20 WGS assemblies. Empirical stringencies were computed as the quotients of the numbers of gaps in the assembly and a theoretical maximum, while the coverages were based on the numbers of reads in an assembly (further details in Wendl and Yang, 2004).
4. Repetitive elements and estimation of genome length
Repetitive elements are among the most frequent dynamic features of the genome. Many of them display complicated evolutionary dynamics (for some models, see e.g., Kimmel and Axelrod, 2002). Here, mostly based on Li and Waterman (2003), we review the influence of repetitive elements on estimation of genome length. In the shotgun sequencing method, the genomic sequence is assembled from overlapping fragments. Uncertainties of the assembly (see further on) lead to the need to analyze the repeat structure of the sequence to be able to estimate the true size of the genome or its fragment sequenced. Indeed, let us consider a given DNA sequence. If we can choose l such that almost all l -mers appear only once in the sequence, if they appear at all, then, by counting how many different l -mers there are in the fragments, we can have a good estimate of the length of the sequence. This is accurate, assuming that the sequence is random with letters generated independently. However, there may be many repeats in the sequence (Primrose, 1998), such that many l-mers appear in it twice or more, even if l is quite large. In this case, the number of different l-mers in the fragments should be much smaller than the number of nucleotides in the sequence. However, if we know how many times each l-mer is repeated, and what fraction of the sequence it accounts for, we can estimate the sequence length. That is, we may have to estimate the repeat structure and coverage in order to estimate the sequence length.
Recall that, for an l-mer appearing in a sequence, instead of the number of this l-mer’s occurrences in this sequence, we obtain the number of this l -mer’s occurrence in N fragments. Because the fragments are randomly chosen from clone libraries, their positions in the original sequence are random, as is the number of occurrences of any l-mer in the sequence. Let us consider the distributions of these random variables first. Assume we know the coverage a of the genome by these N fragments. Also assume that an l-mer in the sequence cannot appear twice or more in any fragment, that is, any two copies of an l-mer are at least L base pairs apart in the original sequence. For a given l-mer, for instance, w, that appears in the sequence n(w) times, how many times will it appear in N fragments?
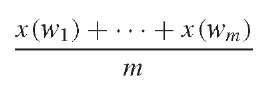
Assume x;(w) is the number of fragments that cover the ith copy of w, in which i is from 1 to n(w). Then, w appears xn(w)(w) times in the fragments. Note that x>(w), i = 1, … , n(w) are independent identically distributed (i.i.d.) and approximately Poisson. Assume the parameter of the Poisson process is X
(Lander and Waterman, 1988). The distribution of xi(w) is Poisson with parameter X (L – l + 1). Owing to the additivity of Poisson process, the distribution of x(w) is Poisson with parameter n (w) X (L – l + 1). For any given l -mer w in the sequence, we do not have a vector of (xi(w), i = 1, … , n(w)}, but x(w), the sum of the elements in the vector. For estimation, we can use all observations from those l-mers, that appear approximately n = n (w) times in the original sequence, as samples of w (family n). Recall that the number of occurrences of those l-mers may not be independent, although they have the same distribution. Assume w1, w2, … , wm are those family n l-mers. We have
approach n (w) X (L – l + 1) when m is large.
Assume there are k families of l-mers in the original sequence, the number of occurrences of any l-mer in the fragments from the i th family is a Poisson random variable with parameter ai a, in which a = X (L – l + 1) is the coverage and ai is an unknown integer. Different l-mers in the ith family account for ai x 100% of all different mers in the original sequence. Mathematically, we have a set of samples from a mixture of Poisson distributions, and some of the samples are dependent. We estimate ai, ai, and a for i = 1,2, … , k. For this mixed-Poisson proportion problem, we get the following expressions (Lange, 1998)
We have no data for w with n(w) = 0. That is, we do not know group 0 if we assume that there are group i -mers in the sequence, which appear i times in the fragments, for i =0, … , groupNum. But, we can use the following formulas to estimate group 0.
According to Li and Waterman (2003), the length of the sequence is estimated by the second or third expression below.
or
The expressions developed can be used to create a recursive algorithm of the Expectation-Maximization (EM) type. This first entails setting a large number for k and a proper number for l and calculation of group(j), for j = 1, 2, … , groupNum, based on data. Then, we set initial values for ai, a, and ai, respectively for i = 1, 2, … , k. Subsequently, we compute group (0) and new values for ai; a, and ai, respectively for i = 1,2, … , k, based on the expression above. We repeat this step until convergence is reached. Finally, we calculate the percentage of each family of substrings and the length of the sequence.
The proper choice of l is critical for the functioning of the method. As stated above, we should let l be large enough so that many l -mers in the original sequence are unique l-mers. That is, when the DNA is G base pairs (bp) long, l should satisfy 4l > G if the sequence is generated from a uniform i.i.d. mechanism. On the other hand, we cannot let l be too large. For instance, if we let l = L, then there are N l-mers in all, and each l -mer appears once in the fragments in general. Then, our estimate of a is 1, which is incorrect. Moreover, the larger l is, the fewer the number of samples, and the less accurately we can estimate a;, a, and ai, for i = 1,2, … , k. Therefore, l must be large, but not too large. Further details can be found in Li and Waterman (2003).
Statistical properties of this algorithm do not seem to be well developed. Estimation of group(0) is based on the Poisson assumption. Figure 2 of Mullikin and Ning (2003) shows a frequency graph of the 17-mer word occurrence, based on mouse a = 7.5 assembly. It shows a large excess of single-occurrence words above the model curve, indicating that these words are bad data resulting from sequencing errors.
5. Examples of estimation of repeat structure and genome length
Li and Waterman (2003) provide examples of how their method functions. Their Example 3 assumes G = 80 000, L = 500, and a = 3. There are two families of repeats. One is 6-kb long with 2 copies, whereas the other is 1-kb long with 12 copies. Repeats appear in tandem in the original sequence. In more than 95% of the simulations, they observed that the estimated genome length is 73 104 bp; the estimated coverage is 3.283; the unique sequence accounts for 82.7% of the genome. There is only one family of repeats, which has 12 copies and accounts for 17.3% of the sequence. This example illustrates difficulties inherent when short genomes and low coverages are considered. Further details are discussed in Li and Waterman (2003).
6. Polymorphisms
The following is mostly based on Fasulo et al. (2002). Polymorphisms are differences in variants of DNA sequences present in different individuals and on paternal and maternal chromosomes in a single individual. Most algorithms for large-scale DNA assembly make the simplifying assumption that the input data is derived from a single homogeneous source. Frequency of polymorphisms (single nucleotide polymorphisms (SNP), variable-length microsatellites or block insertions and deletions (indels)) depend on the evolutionary history of the species. For example, indels are twice as frequent in the human genome than in the Drosophila genome. Discrepancies due to polymorphisms will cause false negatives in the overlap relations among fragments and may result in confusing the polymorphisms with evolutionary divergence in repeat regions of the genome. The Celera Assembler (Myers et al., 1995) includes the A-statistic, which can help determine if the region containing the bubble seems repetitive. A sequence of overlapping fragments (for simplicity assumed to have equal lengths) of a genomic sequence can be depicted using a directed graph, which is linear for an unambiguous complete assembly. Polymorphisms will be represented as bubble-like structures (for examples, see Fasulo et al., 2002). Bubbles can be resolved in two ways: (1) A single path through the bubble can be designed, resulting in a consensus sequence. (2) Multiple alternative paths may be accepted and represented in the final assembly. An algorithm for bubble resolution (smoothing), which is a subroutine of the Celera Assembler, is described in Fasulo et al. (2002). The final validation of bubble smoothing is resequencing of the putative polymorphisms.
7. Bias in AT versus GC composition
It is known that high AT contents of the genome degrades the quality of assembly. Wendl and Yang (2004) provide a semiempirical relationship for stringency in prokaryotes aemp = 1.129 exp(-4.93y), where y is the GC content, with correlation of around 76%. Analogous relationship in eukaryotes is not so well defined.
8. Annotation by words and comparison of genome assemblies
It is possible to annotate large genomic sequences with exact word matches. Healy et al. (2003) developed a tool for rapidly determining the number of exact matches of any word within large, internally repetitive genomes or sets of genomes. This is achieved by creating a data structure that can be efficiently queried and that can also entirely reside in random access memory (RAM). The solution depends upon the Burrows-Wheeler transform, a method used to create a reversible permutation of a string of text that tends to be more compressible than the original text (Burrows and Wheeler, 1994). First, given a genome G of length G, we create a new string G$ of length G + 1 by appending a “$” to the end of that genome. We then generate all G + 1 “suffixes” of G$, that is, substrings that start at every position and proceed to the end. We next associate with each suffix the letter preceding it. In the case of the suffix that starts at the first position, we associate the new $ character and assume that “$” has the lowest lexicographical value in the genome alphabet. The string of antecedent letters, in the lexicographical order of their suffixes, is the Burrows-Wheeler transform of the G$ string. For example, if the genome were simply “CAT”, the G$ string would be “CAT$”. Then the suffixes of the genome in sorted order would be: “$”, “AT$”, “CAT$”, and “T$”. The Burrows-Wheeler transform of this particular G$ would be the letters that precede each of these suffixes taken in the same order, specifically “TC$A”. The list of pointers taken in the order of the sorted suffixes would be (3,1,0,2). This list of pointers is the suffix array for the string “CAT$”. The suffix array for the human genome approximately constitutes 12 Gb (3 billion, 4-byte integers) of RAM. However, the B-W string alone is sufficient to determine word counts and it can be compressed to about 1 Gb of RAM. Furthermore, for querying, all but a negligibly small portion of the compressed form can remain so throughout execution (Healy et al., 2003).
Using the above tools, any region of the genome can be annotated with its constituent mer frequencies. Healy et al. (2003) have depicted annotations of a 5kb region of chromosome 19 four-mer lengths, 15, 18, 21, and 24 bases. For each coordinate and each word length, they determined the count of the succeeding word of the given length, in both the sense and antisense directions. One of the most striking features of this terrain is the presence of narrow spikes in 15-mer counts. This is a virtually universal property of all regions of the human sequence examined, including coding exons and it is statistically significant (based on a comparison with random genomes). Hypothetically, these spikes might result from the accidental coincidence of 15-mers in ordinary sequence with 15-mers present in high-copy-number repeats.
Another application of the method was to monitor successive human genome assemblies. Healy et al. (2003) compared December 2001 and June 2002 assemblies and found that, unexpectedly, 1.2% of their probe words vanished from the June 2002 assembly (i.e., all of their constituent 21-mers went from copy number one in their original assembly, to copy number zero in a subsequent assembly). Systematic studies revealed both losses and gains of single-copy words between assemblies. Although there may be technical reasons explaining the dropout of some of these fragments, such as difficulty in assembly or poor-quality sequence, it is also likely that, due to insertion/deletion and order-of-sequence polymorphisms in humans, no fixed linear rendition of the genome is feasible. A detailed discussion is provided in Healy et al. (2003).
9. Examples
The following examples illustrate the complex nature of global-level organization of human chromosomes and demonstrate that the theory developed above is important for the applications. Recently, edited sequences of human chromosome 14 and of the male-specific region of chromosome Y (MSY) were published (Heilig et al., 2003; Skaletsky et al., 2003). In chromosome 14, an ancient duplication involving 70% of chromosome 14 and a portion of chromosome 2 has been reported. This event is, however, only visible at the protein level and predates the mouse – human separation. Heilig et al. (2003) found that 1.6% of chromosome 14 consists of interchromosomal segmental duplications contained in fragments of 1 kb or more that show at least 90% sequence identity. On the basis of further references in Heilig et al. (2003), comparable value, based on a different comparison procedure, was reported earlier, and confirms that chromosome 14 has the lowest content of interchromosome segmental duplications in the human genome. In a similar analysis that excluded repetitive DNA, it was found that internal duplications account for 1.1% of chromosome 14 and are clustered in four segments. The largest includes an 800-kb region adjacent to the centromere, which is also part of the segmental duplication shared with chromosome 22.
The male-specific region of the Y chromosome, the MSY, differentiates the sexes and comprises 95% of the chromosome’s length. Skaletsky et al. (2003) determined, among others the most pronounced structural features of the ampliconic regions of Y are eight massive palindromes. In all eight palindromes, the arms are highly symmetrical, with arm-to-arm nucleotide identities of 99.94-99.997%. The palindromes are long, their arms ranging from 9 kb to 1.45 Mb in length. They are imperfect in that each contains a unique, nonduplicated spacer, 2-170kb in length, at its centre. Palindrome P1 is particularly spectacular, having a span of 2.9 Mb, an arm-to-arm identity of 99.97%, and bearing two secondary palindromes (P1.1 and P1.2, each with a span of 24 kb) within its arms. The eight palindromes collectively comprise 5.7 Mb, or one-quarter of the MSY euchromatin.
In addition to palindromes and inverted repeats, the ampliconic regions of Yq and Yp contain a variety of long tandem arrays. Prominent among these are the newly identified NORF (no long open reading frame) clusters, which in aggregate account for about 622 kb on Yp and Yq, and the previously reported TSPY (testis specific protein Y) gene clusters, which comprise about 700 kb of Yp. The NORF arrays are based on a repeat unit of 2.48 kb. Numerous further structural features of MSY and their evolutionary explanations, are discussed in Skaletsky et al. (2003).
10. Concluding remarks
As more and more genomes become sequenced, structural features such as repeated regions, short repeats (mini- and microsatellites), palindromes, and polymorphisms are emerging (for the human Y chromosome example, see Skaletsky et al., 2003). Current understanding of genome assembly has been dominated by practical considerations. In particular, sequencing is time consuming and constrained by cost-efficiency. However, shotgun sequencing also is a stochastic procedure and therefore even edited genome assemblies may contain inaccuracies (Healy et al., 2003). On the other hand, stability of a genome as a whole is not a priori known and may be less perfect than expected (Healy et al., 2003). These observations underscore the need for methods, such as Li and Waterman (2003) algorithm, to estimate structural features of the genome on the basis of reads available. More generally, further mathematical work seems to be needed, transcending the existing theory (see, e.g., Lander and Waterman, 1988), to understand the uncertainties of genome assembly.