1. Introduction
Gene prediction is the process of inferring the sequence of the functional products encoded in genomic DNA sequences. In this chapter, we will review computational methods to predict protein-coding genes. These methods are usually limited to the prediction of the coding fraction of the genes and they ignore for the most part the prediction of the terminal 5′ and 3′ untranslated regions.
In the eukaryotic cell, the pathway leading from the DNA sequence of the genome to the amino acid sequence of the proteins proceeds in a number of steps. A gene sequence is first transcribed into a pre-mRNA sequence, this transcript is subsequently processed (i.e., capped, spliced, and polyadenylated), and the mature mRNA transcript is then transported from the nucleus into the cytoplasm for translation into a functional protein. A number of sequence motifs in the primary DNA sequence or in the intermediate RNA sequences are recognized along this pathway: promoter elements that indicate the site for the initiation of the transcription, splice sites that define the boundaries of the introns removed during splicing, and the initiation and termination codons that define the segment of the mature mRNA translated into protein. A natural approach is for computational gene-prediction methods to attempt to model these sequence motifs, and the mechanism by means of which they are recognized. However, known sequence motifs involved in gene specification carry not enough information to precisely elucidate eukaryotic gene structures, and current computational methods need to rely on additional information such as sequence compositional bias and similarity to known coding sequences. With the flowering of eukaryotic sequencing, genome comparisons have also recently emerged as a powerful approach for eukaryotic gene prediction.
In summary, gene-finding programs predict genes in genomic sequences by a combination of one or usually more of the following approaches:
1. analysis of sequence signals potentially involved in gene specification
2. analysis of regions showing sequence compositional bias correlated with coding function
3. comparison with known coding sequences (proteins or cDNAs)
4. comparison with anonymous genomic sequences.
The so-called ab initio or de novo gene predictors combine approaches 1 and 2. We will term here methods relying mostly in approach 3 as “homology-based” gene predictors, and those mostly based on approach 4 as “comparative” gene predictors. There is not, however, a widely accepted terminology, and, for instance, “comparative” gene predictors are often included within the “de novo” category to separate them from those methods relying on expression data (proteins or cDNAs). Moreover, as programs become increasingly complex, the frontiers between the different categories become very fuzzy, with systems existing nowadays that employ all of the strategies enumerated above.
In this article, we will first review methods to identify sequence signals and to capture the sequence composition bias characteristic of protein-coding regions. We will then describe how these methods are integrated in “ab initio” gene finders, and how these are extended into homology-based and comparative predictors.
2. Prediction of signals
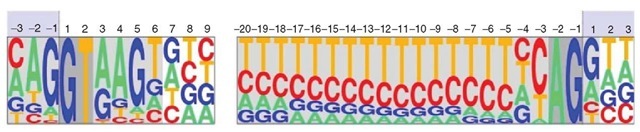
Splice sites (donor and acceptor), translation initiation, and termination codons are the basic sequence signals involved in the definition of coding exons. Typically, these signals are modeled as position weight matrices (PWMs, see Figure 1). The coefficients in these matrices are the observed probabilities in known functional sites of each nucleotide at each position along the signal. Assuming independence between positions, PWMs can be used to compute along a genomic interval the probability of the sequence at a given position assuming that it corresponds to a functional site. Those positions in which this probability is much larger than the background probability of the sequence are typically predicted as potential functional sites. However, because of the degeneracy of the signals, usually many more sites are predicted to be functional than actually are.
To improve signal prediction, methods have been developed that relax the assumption of independence between adjacent positions. In the so-called first-order Markov or weight array model (Zhang and Marr, 1993), the probability of a nucleotide at a given position is conditioned on the nucleotide at the preceding position. Higher-order Markov models – in which the probability at one position is conditioned to a number of preceding positions – have also been considered (see, for instance, Salzberg et al., 1998). Dependencies, however, may not be limited to adjacent positions along the signal. Nonlocal dependencies are implicit in the maximal dependence decomposition (MDD) method (Burge and Karlin, 1997), which has been applied to the prediction of donor sites. More recently, methods based on Bayesian networks, and other probabilistic frameworks, that attempt to systematically recover all relevant dependencies between positions in sequence signals, have been developed for the prediction of splice sites (see, for instance, Castelo and Guigo, 2004). Machine-learning techniques, which capture nonlocal dependencies, have been applied to the prediction of sequence signals as well. The NetGene program (Brunak et al., 1991) is an early example of the application of neural networks (see Article 98, Hidden Markov models and neural networks, Volume 8) to splice site prediction. See Article 16, Searching for genes and biologically related signals in DNA sequences, Volume 7 and Article 28, Computational motif discovery, Volume 7 for a more in-depth review of methods to predict sequence signals.
Figure 1 Sequence logo displaying the position weight matrices (PWMs) corresponding to the canonical donor and acceptor sites of U2 eukaryotic introns. The height of each letter at each position along the site is proportional to the frequency of the corresponding nucleotide as observed in real splice sites. The deviation from random composition can be used to develop methods to predict splice sites.
Despite the variety of efforts, prediction of splice sites (and of other signal sequences) remains an elusive problem. In this regard, recent research suggests that signals other than those at the splice sites play a role in the definition of the intron boundaries. Computational analysis have revealed enhancer sequences that promote splicing of introns with constitutively weak sites, as well as repres-sor sequences that would prevent splicing of “pseudoexons” with otherwise strong splice signals. See Article 24, Exonic splicing enhancers and exonic splicing silencers, Volume 7 for a more in-depth review of exonic splicing enhancers.
3. Prediction of coding regions
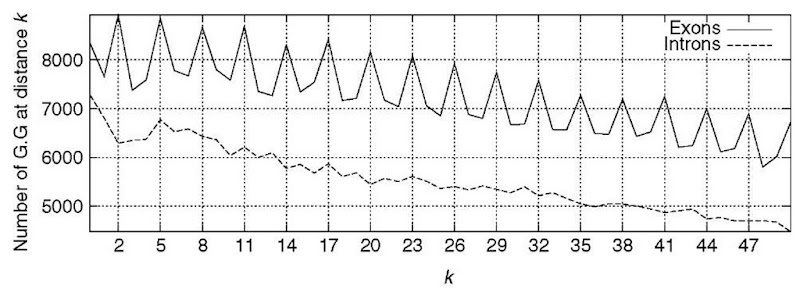
Protein-coding regions exhibit characteristic DNA sequence composition bias, which is absent for noncoding regions (Figure 2). The bias is a consequence of (1) the uneven usage of the amino acids in real proteins, (2) the uneven usage of synonymous codons, and (3) dependencies between adjacent amino acid residues in proteins. To discriminate protein coding from noncoding regions, a number of content measures can be computed to detect this bias (see Guigo, 1999). Such content measures – also known as coding statistics – can be defined as functions that compute a real number related to the likelihood that a given DNA sequence codes for a protein (or a fragment of a protein). Since the early eighties, a great number of coding statistics have been published in the literature. Hexamer frequencies usually in the form of fifth-order Markov Models (Borodovsky and Mclninch, 1993) appear to offer the maximum discriminative power, and are at the core of most popular gene finders today. Combination of a number of coding statistics, on the other hand, seem to improve performance, as in the pioneer GRAIL program (Uberbacher and Mural, 1991).
Figure 2 The absolute frequency of the pair G … G with k (from 0 to 50) nucleotides between the two A’s in the 200 first base pairs accumulated in a set of 1753 human exons and introns. A clear period-3 pattern appears in coding regions, which is absent in noncoding regions. This periodic pattern is a reflection of the characteristic codon usage that can be used to distinguish coding from noncoding regions.
4. “Ab intitio” gene prediction
Most existing computational gene-prediction programs combine at least prediction of sequence signals and prediction of coding regions. Typically, these programs carry out the following tasks: (1) identification of splice sites and other exon-defining sequence signals, (2) prediction of candidate exons based on the predicted signals, (3) scoring of the exons as a function, at least, of the score of the defining signals and the coding statistics computed on the exon sequence, and (4) assembling of a subset of the predicted exons into an “optimal” gene structure – usually the gene structure that maximizes a given scoring function. If this is a linear function of the exon scores, a computational technique known as dynamic programming (see Article 26, Dynamic programming for gene finders, Volume 7) is able to find the solution very efficiently. The programs GENEID (Guigo et al., 1992) and FGENESH (Solovyev et al., 1995) use this approach explicitly. Under the assumption of linearity in the scoring schema, hidden Markov models (HMMs, see Article 98, Hidden Markov models and neural networks, Volume 8) offer a robust framework where the optimal structure can also be obtained very efficiently, with the advantage that it has a precise probabilistic interpretation. Since the development of GENSCAN (Burge and Karlin, 1997), a program that has been widely used in the annotation of vertebrate genomes, HMMs have been very popular for gene finding. Pioneer HMM gene finders include GENIE (Kulp et al., 1996) and HMM-gene (Krogh, 1997).
5. Homology-based gene prediction
When the query genomic sequence encodes genes with known protein or expressed sequence tag (EST) homologs, this information can be used to improve the predictions. One approach is to incorporate in the exon-scoring schema of an underlying “ab initio” program the quality of the alignment between a putative exon and known coding sequences. GENOMESCAN (Yeh et al., 2001), an extension of GENSCAN, among others, incorporates protein similarity, while GRAIL-EXP, an extension of GRAIL, is an early example incorporating similarity to ESTs.
When the homology is very strong (or the genomic sequence encodes a known gene or a gene with ESTs), a more sophisticated approach involves aligning the genomic query directly against the known protein or cDNA target. These alignments, often referred to as “spliced alignments” (see Article 15, Spliced alignment, Volume 7), are usually computationally expensive and cannot be used for database searches, requiring the target sequence to be known in advance. PROCRUSTES (Gelfand et al., 1996) and GENEWISE (Birney and Durbin, 1997) are a few examples of this approach.
6. Comparative gene prediction
Comparative (or dual) genome gene predictors rely on the fact that functional regions in the genome sequence – protein-coding genes in particular – are more conserved during evolution than nonfunctional ones. Over the last few years, a number of programs have been developed that exploit sequence conservation between two genomes. A wide variety of strategies has been explored, ranging from complex extensions of the classical dynamic programming algorithm for sequence alignment that allow for heterogeneous models of sequence conservation to extensions of single-genome predictors allowing for the integration of sequence conservation with another genome in the exon-scoring schema. Comparative gene predictors outperform their single genome “ab initio” counterparts, and three such predictors, SGP-2 (Parra etal., 2003), SLAM (Alexandersson etal., 2003), and TWINSCAN (Korf et al., 2001) have been used in the comparative annotation of the human and rodent genomes (mouse, rat papers). SLAM is a pair-HMM-based method (see Article 17, Pair hidden Markov models, Volume 7), in which gene prediction and sequence alignment are obtained simultaneously. TWINSCAN is an extension of GENSCAN, while SGP-2 is an extension of GENEID. The probability scores that these two programs assign to each potential exon are modified by the presence and quality of genome alignments.
As the number of genomes sequenced at different evolutionary distances increases, methods to predict genes on the basis of the analysis of multiple species -and not of two species only – are being investigated. In the so-called phylogenetic hidden Markov models (phylo-HMMs) or evolutionary hidden Markov models (EHMM), a gene-prediction HMM is combined with a set of evolutionary models, thus taking into account that the rate (and type) of evolutionary events differs in protein-coding and noncoding regions. The recent application of phylo-HMMs to gene prediction has produced encouraging results (for instance, Siepel and Haussler, 2004). See Article 27, Gene structure prediction by genomic sequence alignment, Volume 7 for a more in-depth review of comparative gene-prediction methods.
7. Gene prediction in complete genomes
While a number of gene-prediction programs are efficient enough that they can be easily run on complete eukaryotic genomes, integrated pipelines that execute a number of analysis programs and weigh the different sources of evidence provide the most accurate gene annotations on complex genomes.The annotation of the Tetraodon nigroviridis genome used a different pipeline, based on the GAZE system. GAZE (Howe et al., 2002) is a generic framework for the integration of arbitrary gene-prediction data (from sequence signals to complete gene predictions) using dynamic programming. A more in-depth review of gene-finding pipelines can be found elsewhere in this topic.
Integrated pipelines, complemented with comparative gene-prediction programs, appear to provide accurate enough first-pass annotation of complex eukaryotic genomes when good collections of cDNA or EST sequences exist. Coupled with recent advances in pseudogene detection methods, they have reached a point where computational predictions can be used as a hypothesis to drive experimental annotation via systematic RT-PCR.
When the collections of expression data are poor or nonexistent, however, computational predictions are less reliable. For instance, experimental cloning of genes initially predicted in Caenorhabditis elegans revealed at least 50% of incorrect exonic structures (Reboul et al., 2003). The problem is compounded in those cases for which no phylogenetically related genome has been sequenced. The lack of expression data makes it very difficult to estimate the parameters of the gene-prediction programs, and the common practice of using a gene predictor trained on a different, phylogenetically distant species may lead to poor predictions (Korf, 2004). Since a precise assessment of the accuracy of the gene predictions is important, substantial effort has been made during the last decade to develop consistent accuracy metrics and standard datasets. See Guigo and Wiehe (2003) for a review of efforts to evaluate the accuracy of gene-prediction programs.
In summary, while substantial progress has occurred in the field during the last 15 years, computational gene prediction is still an open problem whose solution will require, not only more sophisticated computational methodologies, but a better understanding of the biological mechanisms by which the sequence signals involved in gene specification are processed and recognized in the eukaryotic cell.