INTRODUCTION
A briefing (Allen, 2004) demonstrates the breadth and depth complexity required to address real diplomatic, information, military, economic (DIME) factors for the propagation/evolution of ideas through defined populations. An open mind would conclude that it is possible that multiple approaches may be required for multiple decision makers in multiple scenarios. However, it is in the interests of multiple decision-makers to as much as possible rely on the same generic model for actual computations. Many users would have to trust that the coded model is faithful to process their inputs.
Similar to DIME scenarios, sophisticated competitive marketing requires assessments of responses of populations to new products.
Many large financial institutions are now trading at speeds barely limited by the speed of light. They co-locate their servers close to exchange floors to be able to turn quotes into orders to be executed within msecs. Clearly, trading at these speeds require automated algorithms for processing and making decisions. These algorithms are based on “technical” information derived from price, volume and quote (Level II) information. The next big hurdle to automated trading is to turn “fundamental” information into technical indicators, e.g., to include new political and economic news into such algorithms.
BACKGROUND
The concept of “memes” is an example of an approach to deal with DIME factors (Situngkir, 2004). The meme approach, using a reductionist philosophy of evolution among genes, is reasonably contrasted to approaches emphasizing the need to include relatively global influences of evolution (Thurtle, 2006).
There are multiple other alternative works being conducted world-wide that must be at least kept in mind while developing and testing models of evolution/propagation of ideas in defined populations: A study on a simple algebraic model of opinion formation concluded that the only final opinions are extremal ones (Aletti et al., 2006). A study of the influence on chaos on opinion formation, using a simple algebraic model, concluded that contrarian opinion could persist and be crucial in close elections, albeit the authors were careful to note that most real populations probably do not support chaos (Borghesi & Galam, 2006). A limited review of work in social networks illustrates that there are about as many phenomena to be explored as there are disciplines ready to apply their network models (Sen, 2006).
Statistical Mechanics of Neocortical Interactions (SMNI)
A class of AI algorithms that has not yet been developed in this context takes advantage of information known about real neocortex. It seems appropriate to base an approach for propagation of ideas on the only system so far demonstrated to develop and nurture ideas, i.e., the neocortical brain. A statistical mechanical model of neocortical interactions, developed by the author and tested successfully in describing short-term memory (STM) and electroencephalography (EEG) indicators, is the proposed bottom-up model. Ideas by Statistical Mechanics (ISM) is a generic program to model evolution and propagation of ideas/patterns throughout populations subjected to endogenous and exogenous interactions (Ingber, 2006). ISM develops subsets of macrocolumnar activity of multivariate stochastic descriptions of defined populations, with macrocolumns defined by their local parameters within specific regions and with parameterized endogenous inter-regional and exogenous external connectivities. Parameters of subsets of macrocolumns will be fit to patterns representing ideas. Parameters of external and inter-regional interactions will be determined that promote or inhibit the spread of these ideas. Fitting such nonlinear systems requires the use of sampling techniques.
The author’s approach uses guidance from his statistical mechanics of neocortical interactions (SMNI), developed in a series of about 30 published papers from 1981-2001 (Ingber, 1983; Ingber, 1985; Ingber, 1992; Ingber, 1994; Ingber, 1995; Ingber, 1997). These papers also address long-standing issues of information measured by electroencephalography (EEG) as arising from bottom-up local interactions of clusters of thousands to tens of thousands of neurons interacting via short-ranged fibers), or top-down influences of global interactions (mediated by long-ranged myelin-ated fibers). SMNI does this by including both local and global interactions as being necessary to develop neocortical circuitry.
Statistical Mechanics of Financial Markets (SMFM)
Tools of financial risk management, developed to process correlated multivariate systems with differing non-Gaussian distributions using modern copula analysis enables bona fide correlations and uncertainties of success and failure to be calculated.
Gaussian copulas are developed in a project Trading in Risk Dimensions (TRD) (Ingber, 2006). Other copula distributions are possible, e.g., Student-t distributions. These alternative distributions can be quite slow because inverse transformations typically are not as quick as for the present distribution. Copulas are cited as an important component of risk management not yet widely used by risk management practitioners (Blanco, 2005).
Sampling Tools
Computational approaches developed to process different approaches to modeling phenomena must not be confused with the models of these phenomena. For example, the meme approach lends it self well to a computational scheme in the spirit of genetic algorithms (GA). The cost/objective function that describes the phenomena of course could be processed by any other sampling technique such as simulated annealing (SA). One comparison (Ingber & Rosen, 1992) demonstrated the superiority of SA over GA on cost/objective functions used in a GA database. That study used Very Fast
Simulated Annealing (VFSR), created by the author for military simulation studies (Ingber, 1989), which has evolved intoAdaptive SimulatedAnnealing (ASA) (Ingber, 1993). However, it is the author’s experience that the Art and Science of sampling complex systems requires tuning expertise of the researcher as well as good codes, and GA or SA likely would do as well on cost functions for this study.
If there are not analytic or relatively standard math functions for the transformations required, then these transformations must be performed explicitly numerically in code such as TRD. Then, the ASA_PARALLEL OPTIONS already existing inASA (developed as part of the 1994 National Science Foundation Parallelizing ASA and PATHINT Project (PAPP)) would be very useful to speed up real time calculations (Ingber, 1993). Below, only a few topics relevant to ISM are discussed. More details are in a previous report (Ingber, 2006).
SMNI AND SMFM APPLIED TO ARTIFICIAL INTELLIGENCE
Neocortex has evolved to use minicolumns of neurons interacting via short-ranged interactions in macrocol-umns, and interacting via long-ranged interactions across regions of macrocolumns. This common architecture processes patterns of information within and among different regions of sensory, motor, associative cortex, etc. Therefore, the premise of this approach is that this is a good model to describe and analyze evolution/propagation of ideas among defined populations.
Relevant to this study is that a spatial-temporal lattice-field short-time conditional multiplicative-noise (nonlinear in drifts and diffusions) multivariate Gaussian-Markovian probability distribution is developed faithful to neocortical function/physiology. Such probability distributions are a basic input into the approach used here. The SMNI model was the first physical application of a nonlinear multivariate calculus developed by other mathematical physicists in the late 1970s to define a statistical mechanics of multivariate nonlinear nonequilibrium systems (Graham, 1977; Langouche et al., 1982).
SMNI Tests on STM and EEG
SMNI builds from synaptic interactions to minicolum-nar, macrocolumnar, and regional interactions in neo-cortex. Since 1981, a series of SMNI papers has been developed model columns and regions of neocortex, spanning mm to cm of tissue. Most of these papers have dealt explicitly with calculating properties of STM and scalp EEG in order to test the basic formulation of this approach (Ingber, 1983; Ingber, 1985; Ingber & Nunez, 1995).
The SMNI modeling of local mesocolumnar interactions (convergence and divergence between minicolumnar and macrocolumnar interactions) was tested on STM phenomena. The SMNI modeling of macrocolumnar interactions across regions was tested on EEG phenomena.
SMNI Description of STM
SMNI studies have detailed that maximal numbers of attractors lie within the physical firing space of both excitatory and inhibitory minicolumnar firings, consistent with experimentally observed capacities of auditory and visual STM, when a “centering” mechanism is enforced by shifting background noise in synaptic interactions, consistent with experimental observations under conditions of selective attention (Ingber, 1985; Ingber, 1994).
These calculations were further supported by high-resolution evolution of the short-time conditional-probability propagator using PATHINT (Ingber & Nunez, 1995). SMNI correctly calculated the stability and duration of STM, the primacy versus recency rule, random access to memories within tenths of a second as observed, and the observed 7±2 capacity rule of auditory memory and the observed 4±2 capacity rule of visual memory.
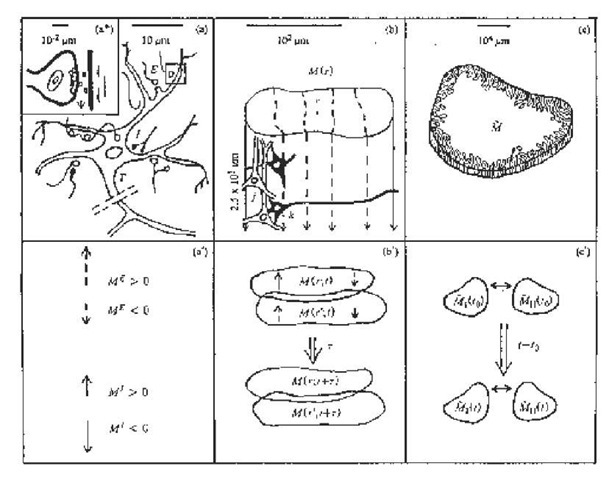
Figure 1. Illustrated are three biophysical scales of neocortical interactions: (a)-(a*)-(a’) microscopic neurons; (b)-(b’) mesocolumnar domains; (c)-(c) macroscopic regions (Ingber, 1983). SMNI has developed appropriate conditional probability distributions at each level, aggregating up from the smallest levels of interactions. In (a*) synaptic inter-neuronal interactions, averaged over by mesocolumns, are phenomenologically described by the mean and variance of a distribution ¥. Similarly, in (a) intraneuronal transmissions are phenomenologically described by the mean and variance of r. Mesocolumnar averaged excitatory (E) and inhibitory (I) neuronal firings Mare represented in (a’). In (b) the vertical organization of minicolumns is sketched together with their horizontal stratification, yielding a physiological entity, the mesocolumn. In (b) the overlap of interacting mesocolumns at locations r and r’ from times t and t + t is sketched. In (c) macroscopic regions of neocortex are depicted as arising from many mesocolumnar domains. (c) sketches how regions may be coupled by long-ranged interactions.
SMNI also calculates how STM patterns (e.g., from a given region or even aggregated from multiple regions) may be encoded by dynamic modification of synaptic parameters (within experimentally observed ranges) into long-term memory patterns (LTM) (Ing-ber, 1983).
SMNI Description of EEG
Using the power of this formal structure, sets of EEG and evoked potential data from a separate NIH study, collected to investigate genetic predispositions to alcoholism, were fitted to an SMNI model on a lattice of regional electrodes to extract brain “signatures” of STM (Ingber, 1997). Each electrode site was represented by an SMNI distribution of independent stochastic macrocolumnar-scaled firing variables, interconnected by long-ranged circuitry with delays appropriate to long-fiber communication in neocor-tex. The global optimization algorithm ASA was used to perform maximum likelihood fits of Lagrangians defined by path integrals of multivariate conditional probabilities. Canonical momenta indicators (CMI) were thereby derived for individual’s EEG data. The CMI give better signal recognition than the raw data, and were used to advantage as correlates of behavioral states. In-sample data was used for training (Ingber, 1997), and out-of-sample data was used for testing these fits. The architecture of ISM is modeled using scales similar to those used for local STM and global EEG connectivity.
Generic Mesoscopic Neural Networks
SMNI was applied to a parallelized generic mesoscopic neural networks (MNN) (Ingber, 1992), adding computational power to a similar paradigm proposed for target recognition.
“Learning” takes place by presenting the MNN with data, and parametrizing the data in terms of the firings, or multivariate firings. The “weights,” or coefficients of functions of firings appearing in the drifts and diffusions, are fit to incoming data, considering the joint “effective” Lagrangian (including the logarithm of the prefactor in the probability distribution) as a dynamic cost function. This program of fitting coefficients in Lagrangian uses methods of ASA. “Prediction” takes advantage of a mathematically equivalent representation of the Lagrangian path-integral algorithm, i.e., a set of coupled Langevin rate-equations. A coarse deterministic estimate to “predict” the evolution can be applied using the most probable path, but PATHINT has been used. PATHINT, even when parallelized, typically can be too slow for “predicting” evolution of these systems. However, PATHTREE is much faster.
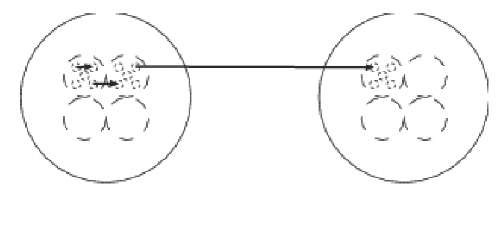
Figure 2. Scales of interactions among minicolumns are represented, within macrocolumns, across macro-columns, and across regions of macro columns
Architecture for Selected ISM Model
The primary objective is to deliver a computer model that contains the following features: (1) A multivariable space will be defined to accommodate populations. (2) A cost function over the population variables in (1) will be defined to explicitly define a pattern that can be identified as an Idea. A very important issue is for this project is to develop cost functions, not only how to fit or process them. (3) Subsets of the population will be used to fit parameters — e.g, coefficients of variables, connectivities to patterns, etc. — to an Idea, using the cost function in (2). (4) Connectivity of the population in (3) will be made to the rest of the population. Investigations will be made to determine what endogenous connectivity is required to stop or promote the propagation of the Idea into other regions of the population. (5) External forces, e.g., acting only on specific regions ofthe population, will be introduced, to determine how these exogenous forces may stop or promote the propagation of an Idea.
Application of SMNI Model
The approach is to develop subsets of Ideas/macroco-lumnar activity of multivariate stochastic descriptions of defined populations (of a reasonable but small population samples, e.g., of 100-1000), with macrocolumns defined by their local parameters within specific regions (larger samples of populations) and with parameterized long-ranged inter-regional and external connectivities. Parameters of a given subset of macrocolumns will be fit using ASA to patterns representing Ideas, akin to acquiring hard-wired long-term (LTM) patterns. Parameters of external and inter-regional interactions will be determined that promote or inhibit the spread of these Ideas, by determining the degree of fits and overlaps of probability distributions relative to the seeded macrocolumns.
That is, the same Ideas/patterns may be represented in other than the seeded macrocolumns by local confluence of macrocolumnar and long-ranged firings, akin to STM, or by different hard-wired parameter LTM sets that can support the same local firings in other regions (possible in nonlinear systems). SMNI also calculates how STM can be dynamically encoded into LTM (Ingber, 1983).
Small populations in regions will be sampled to determine if the propagated Idea(s) exists in its pattern space where it did exist prior to its interactions with the seeded population. SMNI derives nonlinear functions as arguments of probability distributions, leading to multiple STM, e.g., 7±2 for auditory memory capacity. Some investigation will be made into nonlinear functional forms other than those derived for SMNI, e.g., to have capacities of tens or hundreds of patterns for ISM.
Application of TRD Analysis
This approach includes application of methods of portfolio risk analysis to such statistical systems, correcting two kinds of errors committed in multivariate risk analyses: (E1) Although the distributions of variables being considered are not Gaussian (or not tested to see how close they are to Gaussian), standard statistical calculations appropriate only to Gaussian distributions are employed. (E2) Either correlations among the variables are ignored, or the mistakes committed in (E1) — incorrectly assuming variables are Gaussian — are compounded by calculating correlations as if all variables were Gaussian.
It should be understood that any sampling algorithm processing a huge number of states can find many multiple optima. ASA’s MULTI_MIN OPTIONS are used to save multiple optima during sampling. Some algorithms might label these states as “mutations” of optimal states. It is important to be able to include them in final decisions, e.g., to apply additional metrics of performance specific to applications. Experience with risk-managing portfolios shows that all criteria are not best considered by lumping them all into one cost function, but rather good judgment should be applied to multiple stages of pre-processing and post-processing when performing such sampling, e.g., adding additional metrics of performance.
FUTURE TRENDS
Given financial and political motivations to merge information discussed in the Introduction, it is inevitable that many AI algorithms will be developed, and many current AI algorithms will be enhanced, to address these issues.
CONCLUSION
It seems appropriate to base an approach for propagation of generic ideas on the only system so far demonstrated to develop and nurture ideas, i.e., the neocortical brain. A statistical mechanical model of neocortical interactions, developed by the author and tested successfully in describing short-term memory and EEG indicators, Ideas by Statistical Mechanics (ISM) (Ingber, 2006) is the proposed model. ISM develops subsets of macrocolumnar activity of multivariate stochastic descriptions of defined populations, with macrocolumns defined by their local parameters within specific regions and with parameterized endogenous inter-regional and exogenous external connectivities. Tools of financial risk management, developed to process correlated multivariate systems with differing non-Gaussian distributions using modern copula analysis, importance-sampled using ASA, will enable bona fide correlations and uncertainties of success and failure to be calculated.
KEY TERMS
Copula Analysis: This transforms non-Gaussian probability distributions to a common appropriate space (usually a Gaussian space) where it makes sense to calculate correlations as second moments.
DIME: Represents diplomatic, information, military, and economic aspects of information that must be merged into coherent pattern.
Global Optimization: Refers to a collection of algorithms used to statistically sample a space of parameters or variables to optimize a system, but also often used to sample a huge space for information. There are many variants, including simulated annealing, genetic algorithms, ant colony optimization, hill-climbing, etc.
ISM: An anacronym for Ideas by Statistical Mechanics in the context of the noun defined as: A belief (or system of beliefs) accepted as authoritative by some group or school. A doctrine or theory; especially, a wild or visionary theory. A distinctive doctrine, theory, system, or practice.
Meme: Alludes to a technology originally defined to explain social evolution, which has been refined to mean a gene-like analytic tool to study cultural evolution.
Memory: This may have many forms and mechanisms. Here, two major processes of neocortical memory are used forAI technologies, short-term memory (STM) and long-term memory (LTM).
Simulated Annealing (SA): A class of algorithms for sampling a huge space, which has a mathematical proof of convergence to global optimal minima. Most SA algorithms applied to most systems do not fully take advantage of this proof, but the proof often is useful to give confidence that the system will avoid getting stuck for a long time in local optimal regions.
Statistical Mechanics: A branch of mathematical physics dealing with systems with a large number of states. Applications of nonequilibrium nonlinear statistical mechanics are now common in many fields, ranging from physical and biological sciences, to finance, to computer science, etc.