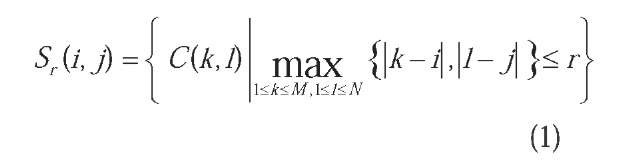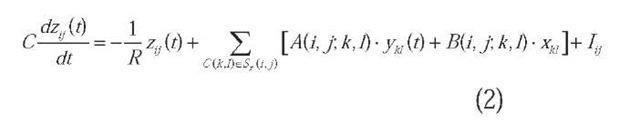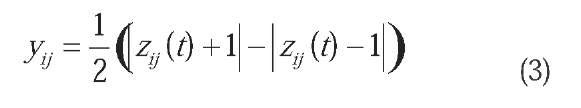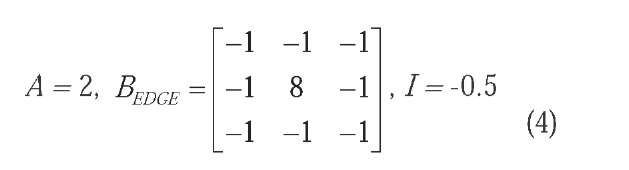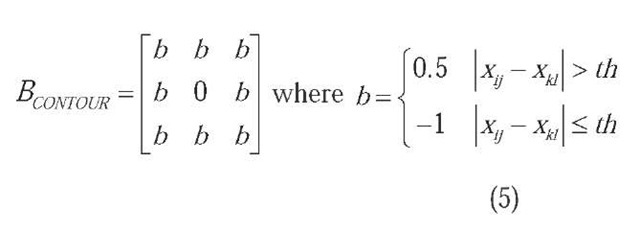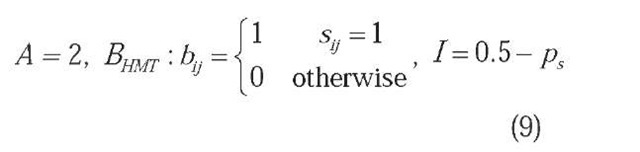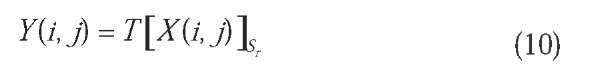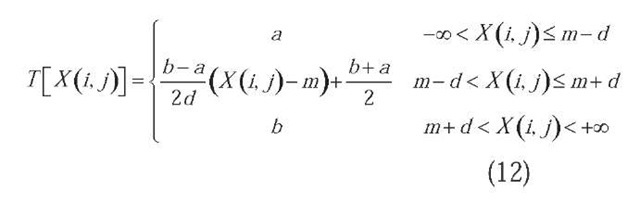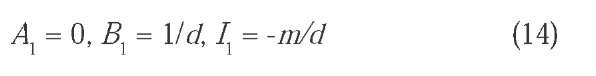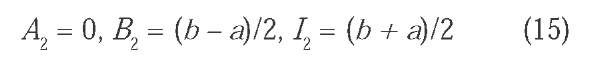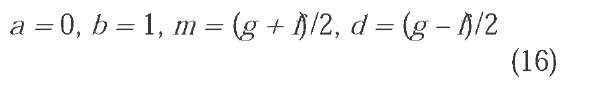INTRODUCTION
Since its introduction to the research community in 1988, the Cellular Neural Network (CNN) (Chua & Yang, 1988) paradigm has become a fruitful soil for engineers and physicists, producing over 1,000 published scientific papers and topics in less than 20 years (Chua & Roska, 2002), mostly related to Digital Image Processing (DIP). This Artificial Neural Network (ANN) offers a remarkable ability of integrating complex computing processes into compact, real-time programmable analogic VLSI circuits as the ACE16k (Rodriguez et al., 2004) and, more recently, into FPGA devices (Perko et al., 2000).
CNN is the core of the revolutionary Analogic Cellular Computer (Roska et al., 1999), a programmable system based on the so-called CNN Universal Machine (CNN-UM) (Roska & Chua, 1993). Analogic CNN computers mimic the anatomy and physiology of many sensory and processing biological organs (Chua & Roska, 2002).
This article continues the review started in this Encyclopaedia under the title Basic Cellular Neural Network Image Processing.
BACKGROUND
The standard CNN architecture consists of an M x N rectangular array of cells C(i,j) with Cartesian coordinates (ij), i = 1, 2, …, M, j = 1, 2, …, N. Each cell or neuron C(ij) is bounded to a sphere of influence 5 (ij) of positive integer radius r, defined by:
This set is referred as a (2r +1) x (2r +1) neighbourhood. The parameter r controls the connectivity of a cell. When r > N/2 and M = N, a fully connected CNN is obtained, a case that corresponds to the classic Hopfield ANN model.
The state equation of any cell C(ij) in the M x N array structure of the standard CNN may be described by:
where C and R are values that control the transient response of the neuron circuit (just like an RC filter), I is generally a constant value that biases the state matrix Z = {z.}, and 5 is the local neighbourhood defined in (1), which controls the influence of the input data X= {x.} and the network output Y = {yj} for time t.
This means that both input and output planes interact with the state of a cell through the definition of a set of real-valued weights, A(i, j; k, l) and B(i, j; k, l), whose size is determined by r. The cloning templates A and B are called the feedback and feed-forward operators, respectively.
An isotropic CNN is typically defined with constant values for r, I, A and B, implying that for an input image X, a neuron C(i, j) is provided for each pixel (i, j), with constant weighted circuits defined by the feedback and feed-forward templates A and B. The neuron state value z.. is adjusted with the bias parameter I, and passed as input to an output function of the form:
The vast majority of the templates defined in the CNN-UM template compendium of (Chua & Roska, 2002) are based on this isotropic scheme, using r = 1 and binary images in the input plane. If no feedback (i.e. A = 0) is used, then the CNN behaves as a convolution network, using B as a spatial filter, /as a threshold and the piecewise linear output (3) as a limiter. Thus, virtually any spatial filter from DIP theory can be implemented on such a feed-forward CNN, ensuring binary output stability via the definition of a central feedback absolute value greater than 1.
ADVANCED CNN IMAGE PROCESSING
In this section, a description of more complex CNN models is performed in order to provide a deeper insight into CNN design, including multi-layer structures and nonlinear templates, and also to illustrate its powerful DIP capabilities.
Nonlinear Templates
A problem often addressed in DIP edge detection is the robustness against noise (Jain, 1989). In this sense, the EDGE CNN detector for grey-scale images given by
is a typical example of a weak-against-noise filter, as a result of fixed linear feed-forward template combined with excitatory feedback. One way to provide the detector with more robustness against noise is via the definition of a nonlinear B template of the form:
This nonlinear template actually defines different coefficients for the surrounding pixels prior to perform the spatial filtering of the input image X. Thus, a CNN defined with nonlinear templates is generally dependent of X, and can not be treated as an isotropic model.
Just two values for the surrounding coefficients of B are allowed: one excitatory for greater than a threshold th luminance differences with the central pixel (i.e. edge pixels), and the other inhibitory, doubled in absolute value, for similar pixels, where th is usually set around 0.5. The feedback template A = 2 remains unchanged, but the value for the bias /must be chosen from the following analysis:
For a given state z.. element, the contribution w.. of the feed-forward nonlinear filter of (5) may be expressed as:
where ps is the number of similar pixels in the 3 x 3 neighbourhood and pe the rest of edge pixels. E.g. if the central pixel has 8 edge neighbours, w.. = 12 – 8 = 4, whereas if all its neighbours are similar to it, then wij = -8. Thus, a pixel will be selected as edge depending on the number of its edge neighbours, providing the possibility of noise reduction. For instance, edge detection for pixels with at least 3 edge neighbours forces that I e (4, 5).
The main result is that the inclusion of nonlinearities in the definition of B coefficients and, by extension, the pixel-wise definition of the main CNN parameters gives rise to more powerful and complex DIP filters (Chua & Roska, 1993).
Morphologic Operators
Mathematical Morphology is an important contributor to the DIP field. In the classic approach, every morphologic operator is based on a series of simple concepts from Set Theory. Moreover, all of them can be divided into combinations of two basic operators: erosion and dilation (Serra, 1982). Both operators take two pieces of data as input: the binary input image and the so-called structuring element, which is usually represented by a 3×3 template.
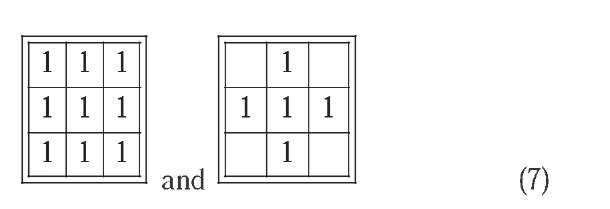
A pixel belongs to an object if it is active (i.e. its value is 1 or black), whereas the rest of pixels are classified as background, zero-valued elements. Basic morphologic operators are defined using only object pixels, marked as 1 in the structuring element. If a pixel is not used in the match, it is left blank. Both dilation and erosion operators may be defined by the structuring elements
for 8 or 4-neighbour connectivity, respectively. In dilation, the structuring element is placed over each input pixel. If any of the 9 (or 5) pixels considered in (7) is active, then the output pixel will be also active (Jain, 1989). The erosion operator can be defined as the dual of dilation, i.e. a dilation performed over the background.
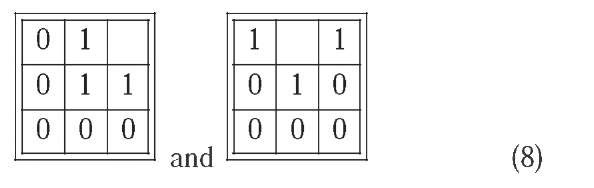
More complex morphologic operators are based on structuring elements that also contains background pixels. This is the case of the Hit and Miss Transform (HMT), a generalized morphologic operator used to identify certain local pixel configurations. For instance, the structuring elements defined by
are used to find 90° convex corner object pixels within the image. A pixel will be selected as active in the output image if its local neighbourhood exactly matches with that defined by the structuring element. However, in order to calculate a full, non-orientated corner detector it will be necessary to perform 8 HMT, one for each rotated version of (8), OR-ing the 8 intermediate output images to obtain the final image (Fisher et al., 2004).
In the CNN context, the HMT may be obtained in a straightforward manner by:
where S = {s.} is the structuring element and ps is the total number of active pixels in it.
Since the input template B of the HTM CNN is defined via the structuring element S, and given that there are 29 = 512 distinct 3 x 3 possible structuring elements, there will also be 512 different hit-and-miss erosions. For achieving the opposite result, i.e. hit-and-miss dilation, the threshold must be the opposite of that in (9) (Chua & Roska, 2002).
Dynamic Range Control CNN and Piecewise Linear Mappings
DIP techniques can be classified by the domain where they operate: the image or spatial domain or the transform domain (e.g. the Fourier domain). Spatial domain techniques are those who operate directly over the pixels within an image (e.g. its intensity level). A generic spatial operator can be defined by
where Xand Tare the input and output images, respectively, and Tis a spatial operator defined over a neighbourhood Sr around each pixel X(i, j), as defined in (1). Based on this neighbourhood, spatial operators can be grouped into two types: Single Point Processing Operators, also known as Mapping Operators, and Local Processing Operators, which can be defined by a spatial filter (i.e. 2D-discrete convolution) mask (Jain, 1989).
The simplest form of Tis obtained when Sr is 1 pixel size. In this case, Yonly depends of the intensity value of X for every pixel and T becomes an intensity level transformation function, or mapping, of the form
where r and s are variables that represent grey level in Xand Y, respectively.
According to this formulation, mappings can be achieved by direct application of a function over a range of input intensity levels. By properly choosing the form of T, a number of effects can be obtained, as the grey-level inversion, dynamic range compression or expansion (i.e. contrast enhancement), and threshold binarization for obtaining binary masks used in analysis and morphologic DIP.
A mapping is linear if its function T is also linear. Otherwise, Tis not linear and the mapping is also nonlinear. An example of nonlinear mapping is the CNN output function (3). It consists of three linear segments: two saturated levels, -1 and +1, and the central linear segment with unitary slope that connects them. This function is said to be piecewise linear and is closely related to the well-known sigmoid function utilized in the Hopfield ANN (Chua & Roska, 1993). It performs a mapping of intensity values stored in Z in the [-1,
+1] range. The bias I controls the average point of the input range, where the output function gives a zero-valued outcome.
Starting from the original CNN cell or neuron (1)-(3), a brief review of the Dynamic Range Control (DRC) CNN model first defined in (Fernandez et al., 2006) follows. This network is designed to perform a piecewise linear mapping Tover X, with input range [m-d, m+d] and output range [a, b]. Thus,
In order to be able to implement this function in a multi-layer CNN, the following constraints must be met:
A CNN cell which controls the desired input range can be defined with the following parameters:
This network performs a linear mapping between [m-d, m+d] and [-1,+1]. Its output is the input of a second CNN whose parameters are:
The output of this second network is exactly the mapping T defined in (12) bounded by the constraints of (13).
One of the simplest techniques used in grey-scale image contrast enhancement is contrast stretching or normalization. This technique maximizes the dynamic range of the intensity levels within the image from suitable estimates of the maximum and minimum intensity values (Fisher et al., 2004). Thus, in the case of normalized grey-scale images, where the minimum (i.e. black) and maximum (i.e. white) intensity levels are represented by 0 and 1 values, respectively; if such an image with dynamic intensity range [f g] c [0, +1] is fed in the input of the 2-layer CNN defined by (14) and (15), the following parameters will achieve the desired linear dynamic range maximization:
The DRC network can be easily applied to a first order piecewise polynomial approximation of nonlinear, continuous mappings. One of the valid possibilities is the multi-layer DRC CNN implementation of error-controlled Chebyshev polynomials, as described in (Fernandez et al., 2006). The possible mappings include, among many others, the absolute value, logarithmic, exponential, radial basis and integer and real-valued power functions.
FUTURE TRENDS
There is a continuous quest by engineers and specialists: compete with and imitate nature, especially some “smart” animals. Vision is one particular area which computer engineers are interested in. In this context, the so-called Bionic Eye (Werblin et al., 1995) embedded in the CNN-UM architecture is ideal for implementing many spatio-temporal neuromorphic models.
With its powerful image processing toolbox and a compact VLSI implementation (Rodriguez et al., 2004), the CNN-UM can be used to program or mimic different models of retinas and even combinations of them. Moreover, it can combine biologically based models, biologically inspired models, and analogic artificial image processing algorithms. This combination will surely bring a broader kind of applications and developments.
CONCLUSION
A number of other advances in the definition and characterization of CNN have been researched in the past decade. This includes the definition of methods for designing and implementing larger than 3×3 neighbourhoods in the CNN-UM (Kek & Zarandy, 1998), the CNN implementation of some image compression techniques (Venetianer et al., 1995) or the design of a CNN-based Fast Fourier Transform algorithm over analogic signals (Perko et al., 1998), between many others.
In this article, a general review of the main properties and features of the Cellular Neural Network model has been addressed focusing on its DIP applications. The CNN is now a fundamental and powerful toolkit for real-time nonlinear image processing tasks, mainly due to its versatile programmability, which has powered its hardware development for visual sensing applications (Roska et al., 1999).
KEY TERMS
Bionics: The application of methods and systems found in nature to the study and design of engineering systems. The word seems to have been formed from “biology” and “electronics” and was first used by J. E. Steele in 1958.
Chebyshev Polynomial: An important type of polynomials used in data interpolation, providing the best approximation of a continuous function under the maximum norm.
Dynamic Range: A term used to describe the ratio between the smallest and largest possible values of a variable quantity.
FPGA: Acronym that stands for Field-Programmable Gate Array, a semiconductor device invented in 1984 by R. Freeman that contains programmable interfaces and logic components called “logic blocks” used to perform the function of basic logic gates (e.g. XOR) or more complex combination functions such as decoders.
Piecewise Linear Function: A function fx) that can be split into a number of linear segments, each of which is defined for a non-overlapping interval of x.
Spatial Convolution: A term used to identify the linear combination of a series of discrete 2D data (a digital image) with a few coefficients or weights. In the Fourier theory, a convolution in space is equivalent to (spatial) frequency filtering.
Template: Also known as kernel, or convolution kernel, is the set of coefficients used to perform a spatial filter operation over a digital image via the spatial convolution operator.
VLSI: Acronym that stands for Very Large Scale Integration. It is the process of creating integrated circuits by combining thousands (nowadays hundreds of millions) of transistor-based circuits into a single chip. A typical VLSI device is the microprocessor.