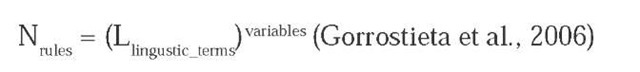INTRODUCTION
Fuzzy logic became the core of a different approach to computing. Whereas traditional approaches to computing were precise, or hard edged, fuzzy logic allowed for the possibility of a less precise or softer approach (Klir et al., 1995, pp. 212-242). An approach where precision is not paramount is not only closer to the way humans thought, but may be in fact easier to create as well (Jin, 2000). Thus was born the field of soft computing (Zadeh, 1994). Other techniques were added to this field, such as Artificial Neural Networks (ANN), and genetic algorithms, both modeled on biological systems. Soon it was realized that these tools could be combined, and by mixing them together, they could cover their respective weaknesses while at the same time generate something that is greater than its parts, or in short, creating synergy.
Adaptive Neuro-fuzzy is perhaps the most prominent of these admixtures of soft computing technologies (Mitra et al., 2000). The technique was first created when artificial neural networks were modified to work with fuzzy logic, hence the Neuro-fuzzy name (Jang et al., 1997, pp. 1-7). This combination provides fuzzy systems with adaptability and the ability to learn. It was later shown that adaptive fuzzy systems could be created with other soft computing techniques, such as genetic algorithms (Yen et al., 1998, pp. 469-490), Rough sets (Pal et al., 2003; Jensen et al., 2004, Ang et al., 2005) and Bayesian networks (Muller et al., 1995), but the Neuro-fuzzy name was widely used, so it stayed. In this chapter we are using the most widely used terminology in the field.
Neuro-fuzzy is a blanket description of a wide variety of tools and techniques used to combine any aspect of fuzzy logic with any aspect of artificial neural networks. For the most part, these combinations are just extensions of one technology or the other. For example, neural networks usually take binary inputs, but use weights that vary in value from 0 to 1. Adding fuzzy sets to ANN to convert a range of input values into values that can be used as weights is considered a Neuro-fuzzy solution. This chapter will pay particular interest to the sub-field where the fuzzy logic rules are modified by the adaptive aspect of the system.
The next part of this chapter will be organized as follows: in section 1 we examine models and techniques used to combine fuzzy logic and neural networks together to create Neuro-fuzzy systems. Section 2 provides an overview of the main steps involved in the development of adaptive Neuro-fuzzy systems. Section 3 concludes this chapter with some recommendations and future developments.
NEURO-FUZZY TECHNOLOGY
Neuro-fuzzy Technology is a broad term used to describe a field of techniques and methods used to combine fuzzy logic and neural networks together (Jin, 2003, pp. 111-140). Fuzzy logic and neural networks each have their own sets of strengths and weaknesses, and most attempts to combine these two technologies have the goal of using each techniques strengths to cover the others weaknesses.
Neural networks are capable of self-learning, classification and associating inputs with outputs. Neural networks can also become a universal function ap-proximator (Kosko, 1997, pp. 299; Nauck et al., 1998, Nauck et al. 1999). Given enough information about an unknown continuous function, such as its inputs and outputs, the neural network can be trained to approximate it. The disadvantages of neural networks are they are not guaranteed to converge, that is to be trained properly, and after they have been trained they cannot give any information about why they take a particular course of action when given a particular input.
Fuzzy logic Inference systems can give human readable and understandable information about why a particular course of action was taken because it is governed by a series of IF THEN rules. Fuzzy logic systems can adapt in a way that their rules and the parameters of the fuzzy sets associated with those rules can be changed to meet some criteria. However fuzzy logic systems lack the capability for self-learning, and must be modified by an external entity. Another salient feature of fuzzy logic systems is that they are, like artificial neural networks, capable of acting as universal approximators.
The common feature of being able to act as a universal approximator is the basis of most attempts to merge these two technologies. Not only it can be used to approximate a function but it can also be used by both neural networks, and fuzzy logic systems to approximate each other as well. (Pal et al., 1999, pp. 66)
Universal approximation is the ability of a system to replicate a function to some degree. Both neural networks and fuzzy logic systems do this by using a non-mathematical model of the system (Jang et al., 1997, pp. 238; Pal et al., 1999, pp. 19). The term approximate is used as the model does not have to match the simulated function exactly, although it is sometime possible to do so if enough information about the function is available. In most cases it is not necessary or even desirable to perfectly simulate a function as this takes time and resources that may not be available and close is often good enough.
Categories of Neuro-Fuzzy Systems
Efforts to combine fuzzy logic and neural networks have been underway for several years and many methods have been attempted and implemented. These methods are of two major categories:
• Fuzzy Neural Networks (FNN): are neural networks that can use fuzzy data, such as fuzzy rules, sets and values (Jin, 2003, pp.205-220).
• Neural-Fuzzy Systems (NFS): are fuzzy systems “augmented” by neural networks (Jin, 2003, pp.111-140).
There also four main architectures used for implementing neuro-fuzzy systems:
• Fuzzy Multi-layer networks (Jang, 1993; Mitra et al., 1995; Mitra et al., 2000; Mamdani et al., 1999; Sugeno et al., 1988, Takagi et al., 1985).
• Fuzzy Self-Organizing Map networks (Drobics et al., 2000; Kosko, 1997, pp. 98; Haykin, 1999, pp. 443)
• Black-Box Fuzzy ANN (Bellazzi et al., 1999; Qiu, 2000; Monti, 1996)
• HybridArchitectures (Zatwarnicki, 2005; Borzem-ski et al., 2003; Marichal et al., 2001; Rahmoun et al., 2001; Koprinska et al., 2000; Wang et al. 1999; Whitfort et al., 1995).
DEVELOPMENT OF ADAPTIVE
neuro-fuzzy systems
Developing an Adaptive Neuro-fuzzy system is a process that is similar to the procedures used to create fuzzy logic systems, and neural networks. One advantage of this combined approach is that it is usually no more complicated than either approach taken individually.
As noted above, there are two methods of creating a Neuro-fuzzy system; integrating fuzzy logic into a neural network framework (FNN), and implementing neural networks into a fuzzy logic system (NFS). A fuzzy neural network isjust a neural network with some fuzzy logic components; hence is generally trained like a normal neural network is.
Training Process: The training regimen for a NFS differs slightly from that used to create a neural network and a fuzzy logic system in some key ways, while at the same time incorporating many improvements over those training methods.
The training process of a Neuro-fuzzy system has five main steps: (Von Altrock, 1995, pp. 71-75)
• Obtain Training Data: The data must cover all possible inputs and output, and all the critical regions of the function if it is to model it in an appropriate manner.
• Create a Fuzzy Logic System: The fuzzy system may be an existing system which is known to work, such as one that has been in production for some time or one that has been created by following expert system development methodologies.
• Define the Neural Fuzzy Learning: This phase deals with defining what you want the system to learn. This allows greater control over the learning process while still allowing for rule knowledge discovery.
• Training Phase: To run the training algorithm. The algorithm may have parameters that can be adjusted to modify how the system is to be modified during training.
• Optimization and Verification: Validation can take many forms, but will usually involve feeding the system a series of known inputs to determine if the system generates the desired output, and or is within acceptable parameters. Furthermore, the rules and membership functions may be extracted so they can be examined by human experts for correctness.
CONCLUSION AND FUTURE DEVELOPMENTS
Advantages of ANFsystems: Although there are many ways to implement a Neuro-fuzzy system, the advantages described for these systems are remarkably uniform across the literature. The advantages attributed to Neuro-fuzzy systems as compared toANNs are usually related to the following aspects:
• Faster to train: This is due to the massive number of connections present in the ANN, and the non-trivial number of calculations associated with each. As well, most neural fuzzy systems can be trained by going through the data once, whereas a neural network may need to be exposed to the same training data many times before it converges.
• Less computational resources: Neural fuzzy system is smaller in size and contains fewer internal connections than a comparable ANN, hence it is faster and use significantly less resources.
• Offer the possibility to extract the rules: This is a major advantage over ANNs in that the rules governing a system can be communicated to the human users in an easily understandable form.
Limitation of ANF systems: The greatest limitation in creating adaptive systems is known as the “Curse of Dimensionality”, which is named after the exponential growth in the number of features that the model has to keep track of as the number of input attributes increases. Each attribute in the model is a variable in the system, which corresponds to an axis in a multidimensional graph that the function is mapped into. The connections between different attributes correspond to the number of potential rules in the system as given by the formula:
This formula becomes more complicated if there are different numbers of linguistic variables (fuzzy sets) covering each attribute dimension. Fortunately there are ways around this problem. As the neural fuzzy system is only approximating the function being modeled, the system may not need all the attributes to achieve the desired results.
Another area of criticism in the Neuro-fuzzy field is related to aspects that can’t be learned or approximated. One of the most known aspects here is the caveat attached to the universal approximation. In fact, the function being approximated has to be continuous; a continuous function is a function that does not have a singularity, a point where it goes to infinity. Other functions thatAdaptive Neuro-fuzzy systems may have problems learning are things like encryption algorithms, which are purposely designed to be resistant to this type of analysis.
Future developments: Predicting the future has always been hard; however for ANF technology the future expansion has been made easy because of the widespread use of its basis technology (neural networks and fuzzy logic). Mixing of these technologies creates synergies as they remediate to each other weaknesses. ANF technology allows complex system to be grown instead of someone having to build them.
One of the most promising areas for ANF systems is System Mining. There exist many cases where we wish to automate a system that cannot be systematically described in a mathematical manner. This means there is no way of creating a system using classical development methodologies (i.e. Programming a simulation.). If we have an adequately large set of examples of inputs and their corresponding outputs, ANF can be used to get a model of the system. The rules and their associated fuzzy sets can then be extracted from this system and examined for details about how the system works. This knowledge can be used to build the system directly. One interesting application of this technology is to audit existing complex systems. The extracted rules could be used to determine if the rules match the exceptions of what the system is supposed to do, and even detect fraud actions. Alternatively, the extracted model may show an alternative, and or more efficient manner of implementing the system.
KEY TERMS
Artificial Neural Networks (ANN): An artificial neural network, often just called a “neural network” (NN), is an interconnected group of artificial neurons that uses a mathematical model or computational model for information processing based on a connectionist approach to computation. Knowledge is acquired by the network from its environment through a learning process, and interneuron connection strengths (synaptic weighs) are used to store the acquired knowledge.
Evolving Fuzzy Neural Network (EFuNN): An Evolving Fuzzy Neural Network is a dynamic architecture where the rule nodes grow if needed and shrink by aggregation. New rule units and connections can be added easily without disrupting existing nodes.
The learning scheme is often based on the concept of “winning rule node”.
Fuzzy Logic: Fuzzy logic is an application area of fuzzy set theory dealing with uncertainty in reasoning. It utilizes concepts, principles, and methods developed within fuzzy set theory for formulating various forms of sound approximate reasoning. Fuzzy logic allows for set membership values to range (inclusively) between 0 and 1, and in its linguistic form, imprecise concepts like “slightly”, “quite” and “very”. Specifically, it allows partial membership in a set.
Fuzzy Neural Networks (FNN): are Neural Networks that are enhanced with fuzzy logic capability such as using fuzzy data, fuzzy rules, sets and values.
Neuro-Fuzzy Systems (NFS): A neuro-fuzzy system is a fuzzy system that uses a learning algorithm derived from or inspired by neural network theory to determine its parameters (fuzzy sets and fuzzy rules) by processing data samples.
Self-Organizing Map (SOM): The self-organizing map is a subtype of artificial neural networks. It is trained using unsupervised learning to produce low dimensional representation of the training samples while preserving the topological properties of the input space. The self-organizing map is a single layer feed-forward network where the output syntaxes are arranged in low dimensional (usually 2D or 3D) grid. Each input is connected to all output neurons. Attached to every neuron there is a weight vector with the same dimensionality as the input vectors. The number of input dimensions is usually a lot higher than the output grid dimension. SOMs are mainly used for dimensionality reduction rather than expansion.
Soft Computing: Soft Computing refers to a partnership of computational techniques in computer science, artificial intelligence, machine learning and some engineering disciplines, which attempt to study, model, and analyze complex phenomena. The principle partners at this juncture are fuzzy logic, neuron-computing, probabilistic reasoning, and genetic algorithms. Thus the principle of soft computing is to exploit the tolerance for imprecision, uncertainty, and partial truth to achieve tractability, robustness, low cost solution, and better rapport with reality.