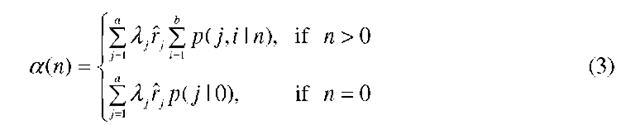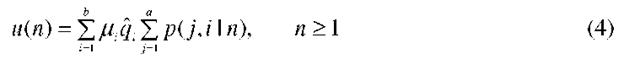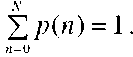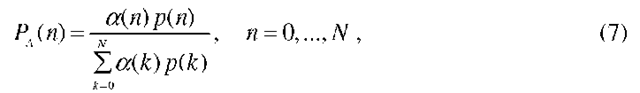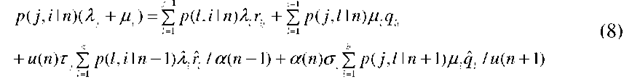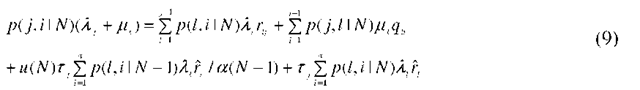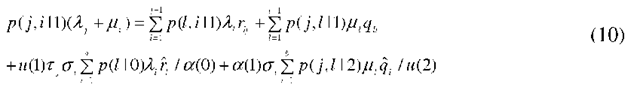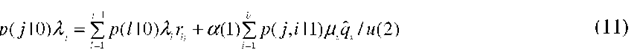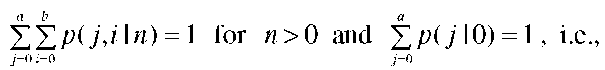Abstract
Queueing delays experienced by packets buffered at a node are among the most difficult to predict when considering the performance of a flow in a network. The arrivals of packets at a node tend to be highly variable so that a finite-buffer single-server queue with general arrivals and service emerges as a natural model of a network link. In this paper we propose an approach to the solution of such a queue when the times between arrivals and service times are represented as acyclic phase-type distributions. The proposed solution approach, based on the use of conditional probabilities, is conceptually simple, easy to implement in a standard computer language, numerically robust and reasonably fast. In addition to standard steady-state probabilities and queue size averages, the proposed approach produces the probabilities of the state of the queue found by an arriving packet, in particular, the packet loss probability, directly linked to the QoS perceived by the user.
Keywords: Capacity planning; buffer sizing; quality of service; modeling; single-server queue; Ph/Ph/1/N queue.
Introduction and State of the Art
When considering the performance of a flow at a network node, queueing delays experienced by packets (or frames) buffered at the node are among the most difficult to predict [23]. Given that a network interface can only transmit one packet at a time, a single-server queue seems a natural model of a network link. There is general agreement that the arrivals of packets at a node are highly variable and a Poisson process is not a valid representation [17, 10, 30]. With variable size packets, the transmission time (service time) is also variable and, generally, not exponentially distributed. Additionally, buffers have finite capacity, sometimes quite small [40], so that the buffer overflow probability and resulting packet loss are of major interest (e.g., because of its effect on TCP congestion window [3]). Hence, the underlying queueing model is a so-called G/G/1/N queue [2].
While the equilibrium solution of the M/M/1/N queue (with Poisson arrivals and exponential service) is straightforward [2], there are no readily usable analytical results for the more realistic G/G/1/N queue. Thus, there are essentially three possible approaches to the solution of such a queue.
The first one is to solve the state equations of the queueing system numerically. A commonly adopted approach is to represent the times between arrivals, as well as the service times, as phase-type distributions [28, 27], and then attempt to solve the resulting balance equations. Here, besides general methods for systems of linear equations (e.g., [35, 12]), which include direct iterative methods (e.g., Gauss-Seidel, over-relaxation [33]), specific approaches for Quasi Birth and Death processes could be used (e.g., Matrix Geometric [27, 26, 24], Spectral Expansion [25]). The latter methods may require a non-trivial degree of mathematical sophistication [15].
The second possible approach is to use discrete-event simulation. While simple in principle, this solution turns out to be fraught with problems. To achieve a reasonable accuracy, serious problems appear when simulating heavy-tailed distributions (such as the Pareto distribution for the time between arrivals) involving rare but important events (cf. [4, 13, 5]). Additionally, the simulation times tend to elongate considerably when the link utilization approaches saturation. As a result, simulation times may become long, making difficult the systematic exploration of a large number of parameter values.
When there is no easy exact solution and the simulation becomes exceedingly long, a natural alternative is to look for simple approximations that would be accurate enough to provide meaningful estimates for delays and loss probabilities. There are several bounds and approximations for the G/G/1 queue with an infinite buffer [21, 22, 34, 37, 2, 19, 9, 31], which may be used to estimate delays for lightly loaded links but not to assess loss probabilities or dimension buffers. There are fewer results for the G/G/1/N queue [20, 38, 39], either limited to the first two moments of the inter-arrival and service times distributions or based on heavy-traffic assumption, which may not be applicable in a realistic network with moderate levels of losses. To the best of our knowledge there are no readily applicable good approximate results for the loss probability.
This paper falls into the first category of approaches. Within the framework of acyclic phase-type representation of general distributions, we propose to use conditional probabilities to obtain a conceptually simple numerical solution that is easy to implement, generally fast, and stable in practice. Our approach allows us to obtain the state probabilities at instants of packet arrival, and hence, the packet loss probability, as well as such customary measures as the expected time in the queue. We have implemented our method in standard C language, and, in the very many test we ran, it performed well, including with phase representations of heavy-tailed distributions.
Our paper is organized as follows. In Section 2 we describe our model and the proposed solution method. Section 3 discusses the practical performance of the method. We use two non-trivial examples to compare the performance of the proposed approach with that of a discrete-event simulation. Section 4 concludes this paper.
Model and Its Solution
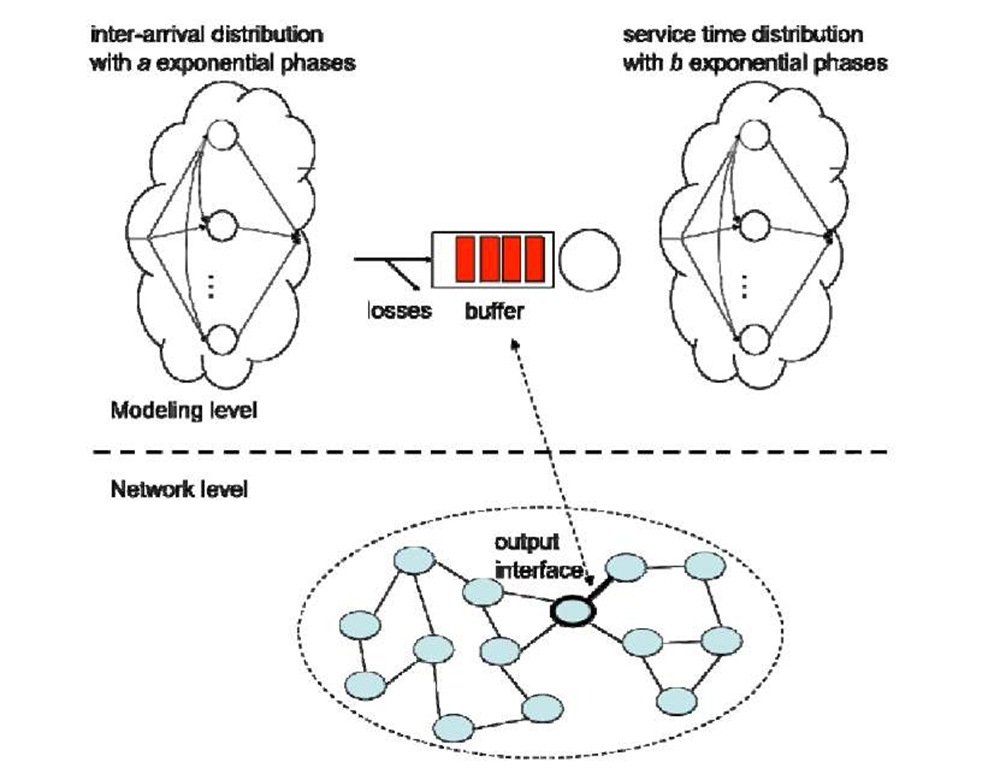
We focus our attention on a single node viewed as a G/G/1/N queue with a FIFO discipline. We adopt the acyclic phase-type representation of the time between arrivals of packets and of their service times. We use the terms requests and packets (or frames) interchangeably. As is well known, any distribution can be approximated arbitrarily closely by a finite number of exponential phases [28, 27], and algorithms exist to represent a given distribution by a phase-type distribution (e.g., [16, 6, 29, 18, 36, 11]). Several authors address more specifically the representation of heavy-tailed distributions (for instance, [16, 18, 11]). Thus, our G/G/1/N model becomes what is known as the Ph/Ph/1/N queue. The advantage of the phase-type representation is that we are able to easily obtain the state equations for our model in the form of the regular balance equations.
Fig. 1. Modeling a network link or an output interface as a Ph/Ph/1/N queue
We denote by a the number of phases in the arrival process, and by b the number of phases in the service process (see Fig. 1). We let be the rate (intensity) of phase j, j = 1,…,a , rjt the probability that phase j is followed by phase I (I > j ), rJ the probability that the arrival process ends after phase j , and Tj the probability that the arrival process starts in phase j . Similarly, for the service process, we denote by / the rate (intensity) of phase i, i = 1,…, b, qu the probability that phase i is followed by phase i ( i > i), q the probability that the service process end after phase i, and cri the probability that the service process starts in phase i, i = 1,…, b. As an example, with a hyper-exponential service time distribution, we have qu = 0 for all values of i and I, and q = 1 for all phases i. Clearly, for any distribution, we must have
A possible state description for the Ph/Ph/l/N queue is p( j, i, n) which is the probability that the arrival process is in its phase j, j = 1,…, a, the service process is in its phase i,i = 1,…,b, and there is a total of n,n = 0,…,N requests in the system (queued and in service). The state probabilities are subject to the normalizing condition
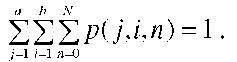The balance equations together with this normalizing condition define a system of linear equations for the probabilities p( j, i, n), and classical numerical solution methods for this type of queueing system seek to solve this system of linear equations as discussed in the Introduction.
We adopt the same basic state description but we use the fact that, from the definition of conditional probability, we have 
where p(n) is the probability that there are n,n = 0,…,N requests in the system, and p( j, i | n) is the conditional probability of the current phases of arrival and service given the number of requests. Note that, for n = 0, the index of the current phase of the service process becomes meaningless, and we write simply p( j 10) to denote the state of the arrival process given that the system is idle.
It is not difficult to show that the probability p(n) can be expressed as
where
is the conditional rate of request arrivals with n requests in the system, and
denotes the conditional rate of request service given n. G is a normalizing constant chosen so that
The probability of a lost request (packet loss probability) can be obtained as
the probability that there is no wait is given by
More generally, we have for the probability that an arriving request finds n requests already present in the system
Thus, to obtain the quantities of interest (such as the loss probability), it suffices to obtain the conditional rates a(n) and u(n), i.e., to solve for the conditional probabilities p(j, i I n). Using the basic identity (1) in the balance equations, we obtain the following system of equations for the conditional probabilities p(j, i I n): for n = 2,…,N -1
for n = N
for n = 1
for n = 0
Note that we have
we have a separate normalizing condition for each value of the number of requests in the system.
We propose a simple iteration akin to a recent iterative method for CVC/c-like queues [8] to solve this system of non-linear equations. Details of this easy-to-implement iteration are given in the topic. In the next section, we apply our approach to study the effect of buffer size on loss probability in a network node. Additionally, we compare the performance of our method with discrete-event simulation when the times between arrivals are represented by a Pareto-like distribution.
Performance of the Proposed Approach
In our first example, we study the performance of our approach using a model of a node with a finite buffer of 50 requests. The request arrival process is represented by a Pareto-like distribution. The latter was obtained using the PhFit package [16], and has a total of 16 exponential phases, 10 of which are used for the heavy-tailed part of the distribution. The parameters of this phase distribution are given in Table 1 in the topic. The service times in our Ph/Ph/1/50 model are represented by a three-phase distribution chosen so as to match the first three moments of a reported packet mix in real networks [1] on a link operating at about 2.5 Gb/s. We used the method proposed by Bobbio et al. [6] to perform the matching of the first three moments. We give in Table 2 in the topic the parameters of the resulting phase distribution.
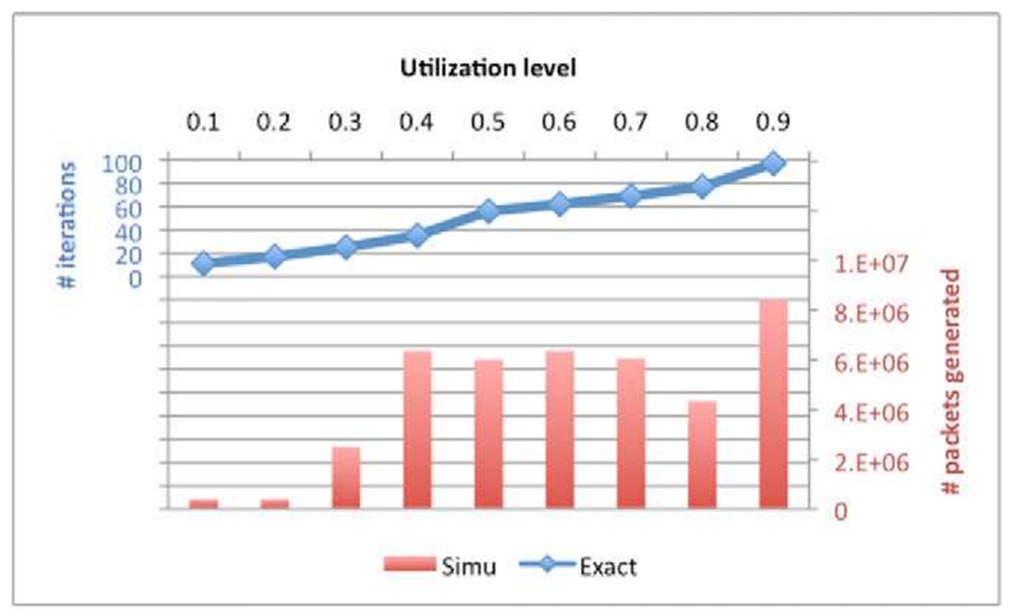
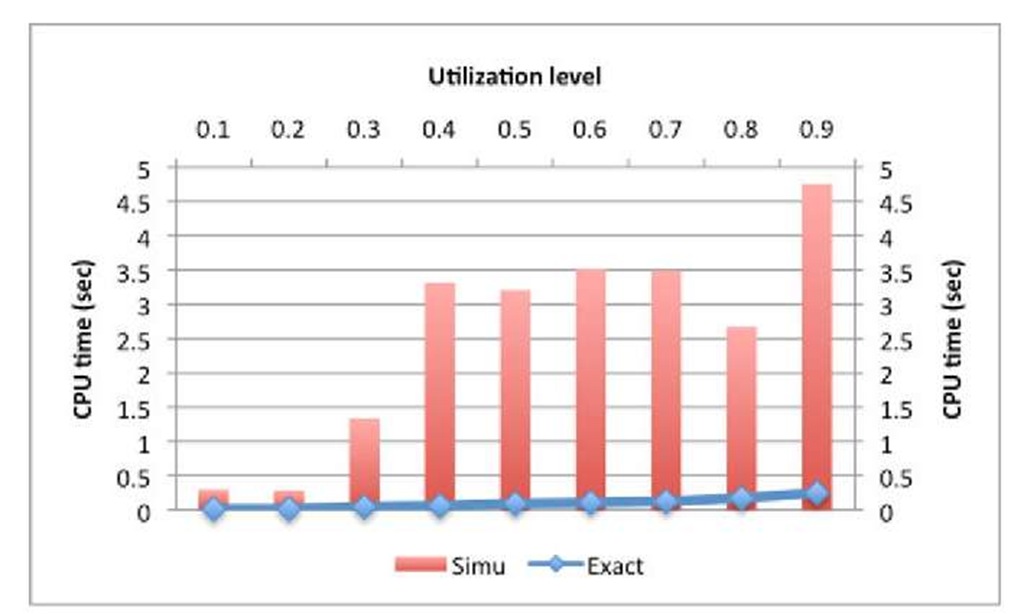
Fig. 2 and Fig. 3 illustrate the results obtained. In all examples we set the convergence stringency of our algorithm at e = 10-7 (increasing the convergence stringency does not change our results). In Fig. 2 we show the number of iterations in our method needed to solve the Ph/Ph/1/50 model for server utilization ranging from 0.1 to 0.9. Fig. 3 displays the execution times of a C implementation on an Intel processor running at 2.2 GHz. For comparison, we include the execution times of a discrete-event simulation of the same model on a processor of the same speed. The simulation has been run long enough to attain a confidence interval of no more than 5% around the exact value of the average number of requests in the queue at 95% confidence level. We used 7 independent replications in our runs.
We observe in Fig. 2 that, for the server utilization levels considered, the proposed method requires only a few tens of iterations (below 100 in all cases). The simulation performance is displayed in terms of the number of packets generated to achieve the desired confidence intervals, and ranges from a total of about 350,000 to 8,000,000 packets. In Fig. 3 we compare the CPU times for both approaches. In the example considered, the CPU time for the proposed solution remains below 0.25 s in all cases. By contrast, the CPU time for the simulation tends to increase significantly as the server utilization increases, exceeding 3 s even for moderate loads. Note that we ran the simulation only for as long as was needed to achieve the desired accuracy, knowing the exact value from our solution method. In practice, one does not know in advance the correct value, so that the simulation needs to be run until the estimated confidence interval at the desired confidence level is sufficiently narrow. This might result in longer simulation times.
Fig. 2. Number of iterations of proposed approach and number of packets generated in simulation vs. link utilization
Fig. 3. CPU time for proposed approach and simulation vs. link utilization
In our second example we apply our approach to study the effect of the buffer size on the packet loss probability in a hypothetical configuration. Obviously, the issue of buffer sizing is not new and has received considerable attention (e.g., [40, 3]). In our hypothetical configuration, the rate of packet arrivals is set to a value such that with unrestricted buffer, i.e., with no packets lost, the resulting link utilization would be 0.8. We keep the same type of Pareto-like arrival process as in our first example. For the service process, we assume a single packet size of 1500 bytes and a link speed of 2.5 Gb/s. We represent the resulting service times as a 10-phase Erlang distribution.
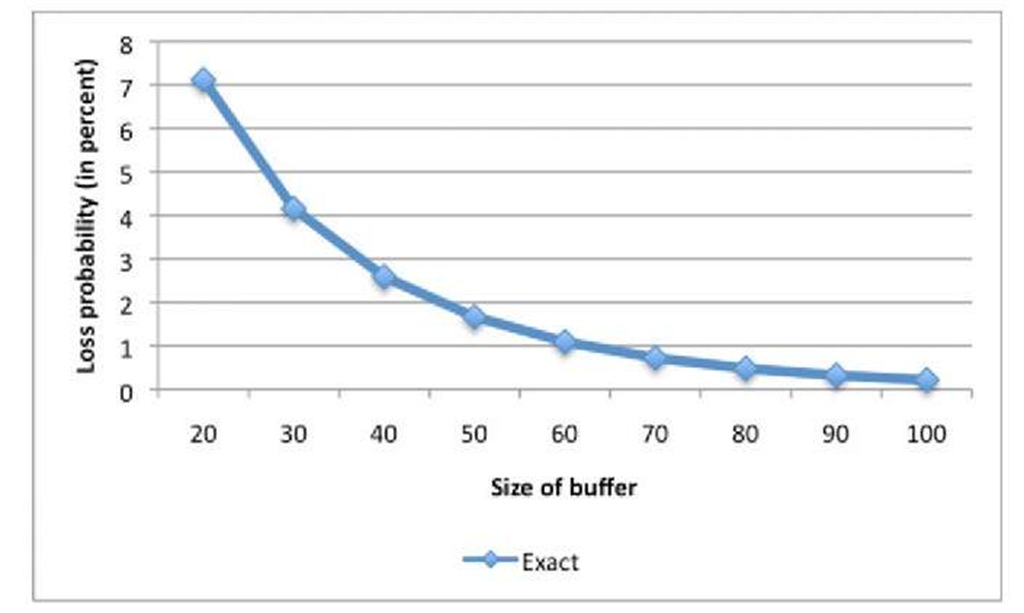
Fig. 4 shows the loss probability as a function of the buffer size obtained using the proposed exact solution of our Ph/Ph/l/N queue. We observe the rapid decrease of losses as the buffer size increases. The ability to predict accurately the loss probability is important to properly size buffers, in particular in the context of TCP [40].
Fig. 4. Predicted loss probability as a function of buffer size
The loss probability estimated by simulation follows the same general pattern. However, as shown in Fig. 7 in the topic, the relative error versus the exact value for the loss probability varies somewhat erratically. The simulation appears to have trouble estimating accurately smaller loss probabilities. We think that this is due to the heavy-tailed nature of the Pareto-like arrival process and the general difficulty of estimating the probability of rare events in a straightforward simulation (similar issues have been pointed out by other authors [4, 13, 5]). If desired, the simulation accuracy could be improved at the expense of non-negligible additional sophistication.
We believe that, given its reasonable speed and conceptual simplicity, the proposed approach offers an attractive alternative to simulation for buffer sizing under non-Poisson assumptions. In that respect, it is worthwhile noting that, for instance, for a buffer size of 80 ( N = 80 ) the proposed solution approach computes some 14000 unknowns (the probabilities p( j, i I n)) in fewer than 100 iterations. Additionally, unlike simulation, analytical or numerical solutions produce directly the desired result and not an estimated confidence interval.
The next section concludes our paper.
Conclusion
In this paper we propose an approach to the solution of a single server queue with a finite buffer and general (but independent) arrivals and service represented through phase-type distributions. Such a Ph/Ph/1/N queue can be viewed as a model of a link or a node in a network. The proposed solution approach is based on the use of conditional probabilities. It is conceptually simple, easy to implement in a standard computer language, numerically robust and reasonably fast.
To deploy our method in practice, one needs to represent the distribution of the times between arrivals and the service time distribution as acyclic phase-type distributions, and then apply our iterative procedure.
In addition to standard steady-state probabilities and queue size averages, the proposed approach produces the probabilities of the state of the queue found by an arriving packet, in particular, the packet loss probability. Note that the state of the queue found by an arriving packet is directly linked to the QoS perceived by the user.
We illustrate the performance of the proposed method using an assumed Pareto-like distribution of the times between arrivals and non-exponential service time distributions. We apply our method to the sizing of a buffer in a hypothetical configuration. Additionally, we compare the performance of the proposed approach with that of a discrete-event simulation. Besides being an order of magnitude faster than the simulation, our exact solution has the advantage of avoiding non-trivial issues that may appear in simulation when dealing with heavy-tailed distribution and rare events.
We believe that the proposed iterative solution for a Ph/Ph/1/N queue is simple enough to be of practical interest for researchers and practitioners who are not necessarily specialists in queueing theory or advanced numerical methods.
