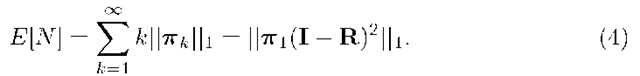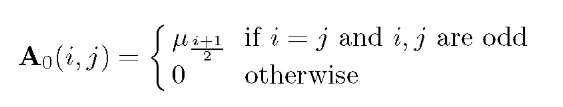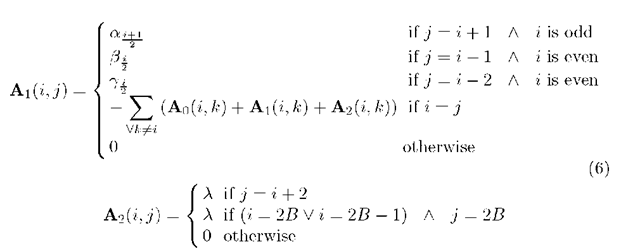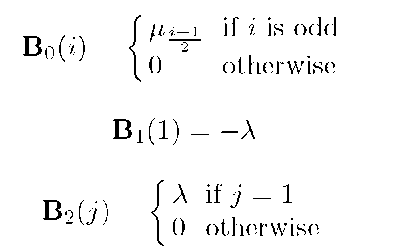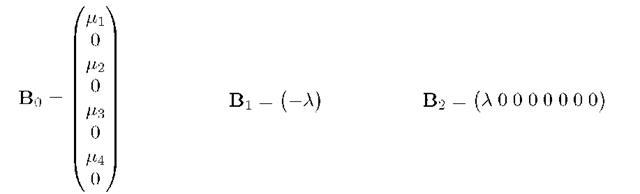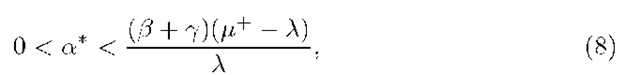Abstract
Garbage collection represents an important feature of many modern systems that allows programmers to avoid explicit memory management and related common errors. However, its usage introduces problems in software performance engineering, because on the one hand the system exhibits better performances when there is low memory occupancy and on the other hand the garbage collection activity blocks other processes, so it may introduce a performance drawback.
We propose a queueing model to analyse a system with a garbage collector, where customers arrive according to a Poisson process and the service time distribution depends on the amount of free memory. Customer arrivals correspond to process activations in the system. The model parameters allow one to specify the garbage collector service rate, and the distribution of the delays between successive activations.
We show that the process underlying such a queueing model is a Quasi-Birth-Death stochastic process and we derive the steady-state analysis via Matrix Geometric Methods. Finally, we propose a heuristic based on this model to derive an appropriate and effective garbage collector activation rate in order to minimise the average system response time. The parametrisation is done using system statistics.
Introduction
In the latest few years memory management in high-level programming languages has been highly improved. In particular, the traditional explicit memory management, which characterises many languages such as C and C++ has shown to be hard to use without introducing serious flaws in the program code. For instance, it may happen that the programmer does not free the memory allocated by an object before the end of the scope of its pointer or, even worse, he/she may refer to objects without allocating them in memory explicitly. The former error leads to the production of the so-called memory garbage, while the latter leads to unexpected program behaviours or even to run-time unrecoverable errors. In order to overcome memory management problems, and to let the programmer focus on the algorithmic aspects of the software, garbage collectors have been introduced. This is a common feature of many high level programming languages based on Virtual machines, such as Java, Microsoft C# but also those based on functional paradigm such as Microsoft F# and O’Caml. Basically, these programming languages abstract out the memory management issues by automatically allocating objects which, in the procedural programming paradigm, are then referred through handles. Handles play the same role of pointers in languages with explicit memory management, but are easier to use and safe, meaning that no unrecoverable run-time errors should occur (and anyway programming flaws are easier to detect). The drawback of this approach is the production of memory garbage (i.e., unreferenced memory blocks) not because of programming flaws, but as a normal activity. In order to avoid a gradual reduction of the available memory, garbage collectors are introduced. A garbage collector is a process that, according to possibly sophisticated algorithms (see, e.g., [4] for a basic review), explores the dynamic memory heap and checks whether an allocated block is referenced by any handle. If an object is not referenced by any handle, then the memory that it uses is marked as free. The non-triviality of the garbage collection algorithms (and also their requirements in terms of CPU usage) is due to the fact that chains or also cycles of objects containing cross-referencing handles may be stored in memory (consider, e.g., a circular list data structure). As a common extension, garbage collectors also compact the occupied memory blocks in order to reduce the fragmentation and allows for wide data structure allocations. This operation may be very time-consuming and can cause a fall of the system performance. Moreover, the activation of the garbage collector causes a partial or full blocking of the execution of the active processes since conflicts in the memory access must be avoided. A challenging problem in the software performance engineering consists in deciding the frequency of the garbage collector activations. Intuitively, a rare activation is desirable in order not to observe a decay of the system response time. Conversely, a lack of garbage collection runs causes the progressive reduction and fragmentation of the memory which leads to virtual memory (and hence disk-swap) need.
Contribution. The scope of this paper is twofold. First, we define a queueing model of the process execution environments in which the garbage collector operates. The queue has an underlying Continuous Time Markov Chain (CTMC) whose regular-block-structure allows the application of Quasi-Birth&Death process analysis [8]. The strength of this approach is that both the derivation of the steady-state probabilities and of the stability condition is fully numerically tractable. We consider the basilar, but still widely applied, garbage collection policy called stop-the-world: in few words, when the garbage collector is activated, the execution of all the other processes is suspended until the execution is over. Obviously, several research efforts have been devoted to relax this strict requirement, e.g., in [10], but, as declared in [11], stop-the-world is a common assumption both for parallel and single-thread garbage collection implementations.
Furthermore, we propose to use the model as the basis to define a heuristic policy to decide on-flight the frequency of garbage collector activation in real systems. We propose to parametrise the model according to a set of measurements which are done during the system working-time and derive an approximation of the optimum frequency of the garbage-collector runs. This policy tends to auto-adapt the system behaviour to the work-load characteristics and does not require a manual tuning of the Virtual Machine parameters which may result difficult also for specialised people.
Related Works. To the best of our knowledge, although several works address the problem of estimating the worsening of the system performance due to garbage collection, our proposed approach is novel. In [4] the authors consider the delays introduced by the garbage collection activity by measurements on real system or simulation. In [3] the authors present a comparison between the explicit memory management mechanisms and the garbage collection with measurements on real systems. We will use this latter paper for a rough validation of our queueing model. Works on the checkpoint interval in databases [2] or on software rejuvenation [12] discuss the optimisation of system availability when some blocking operations are to be executed in order to maintain the system efficiency. None of them, however, considers the problem of garbage collection or uses Quasi-Birth&Death processes. To be best of our knowledge, the usage of a queueing model to estimate the optimal garbage collection rate has not been considered in literature.
Paper Structure. The paper is structured as follows: Section 2 briefly resumes the theoretical background needed to keep the paper self-contained. In particular, Section 2.1 presents Neuts’ matrix geometric method for the analysis of structured Markov chains, and Section 2.2 illustrates its standard application to quasi-birth&death stochastic processes. Section 3 introduces the model for the garbage collector that we present in this paper. In Section 4 we discuss an application of the proposed model to define a heuristic for determining the optimum activation rate in a system with garbage collection. Some numerical examples of applications of such a heuristic are given in Section 5 and, finally, Section 6 presents the conclusion.
Theoretical Background
In this part we recall the fundamental notions required to keep this paper self-contained. We briefly present Neuts’ matrix geometric method for the analysis of structured Markov chains, and then we illustrate its standard application to quasi-birth&death stochastic processes (QBD).
Neuts’ Matrix Geometric Method
Matrix geometric [8,9] is an analysis technique that allows the efficient computation of the steady-state solution of Markov chains with a special structure of the transition rate matrix. In this paper we refer to the case of CTMCs whose infinitesimal generators Q are infinite block tridiagonal matrices with the following structure:
where:
— Ao, Ai, A2 are square matrices with the same dimension C,
— B00 is a square matrix with dimension D,
— Bio is a C x D matrix,
— Boi is a D x C matrix.
Let
be the stationary distribution (assuming it exists) of the CTMC, i.e., 
with the normalising condition
where 1 = (1,1,1,…). Ac cording to the structure of Q, we consider
where
has dimension D, while
have dimension C. Vector
may be iteratively computed with the following scheme:
where
and R are defined as in [8,9]. A faster iterative approach for the computation of R in case of QBD processes is described in [7].
Quasi-Birth and Death Processes
The results presented in this section assume that the infinitesimal generator of the CTMC underlying a queueing system has the tridiagonal structure of (1) and that the
is the steady-state probability of observing exactly i customers in the systems, where \ | \ 1 denotes the 1-norm (or the Taxicab norm) of the vector.
The first interesting problem concerns the decision of the stability of the queue. Let us define A = A0 + A1 + A2 and let
be the solution of
and
Then, for a QBD process to be ergodic, the following condition is required:
For this class of queueing models, we may also derive a closed-matrix-form expression for the mean number of customers in the system:
Since there is no customer loss or creation in the queue, under stability condition the throughput is equal to the arrival rate A, hence by Little’s result we derive the mean response time:
Model Definition and Analysis
This section introduces the model for the garbage collector that we present in this paper.
Model description and underlying assumptions.
1. We consider an infinite set of undistinguishable customers that arrive at the system from the outside according to a homogeneous Poisson process with rate A. Customer arrivals correspond to process activations in the system.
2. If we assume that a customer arrives at an empty system, no other customers arrivals during the service time, and that the garbage collector stays always inactive, then the service time is exponentially distributed and independent of the arrival time.
3. The scheduling discipline is Processor Sharing (see, e.g., [5]). This discipline resembles a Round Robin with pre-emption policy of the system.
4. The memory is divided into B blocks. At each customer arrival epoch, b blocks are occupied, where b is sampled from a discrete random variable with a certain probability distribution. In the rest of the paper we will assume for simplicity that b = 1, but the analysis can be applied for any distribution of b values. It is important to point out that these B blocks are partially allocated in the physical memory and the remaining part in the disk. Therefore, the overall system service rate depends on the amount of available memory. Specifically, in case of usage of disk-allocated memory blocks, the swapping activity, i.e., the passage of memory blocks between the disk to the physical memory and vice-versa, causes a high increase in the customer service time. Hence, the service rate is a function of the occupied memory blocks i, with 0 < i < B. Although it is possible to modify the model in order to consider service rates that depend on the number of customers, this would disrupt the regularity of the resulting matrix structure, and form a so-called Nonhomogeneous QBD process [6], whose solution is computationally challenging.
5. The garbage collector plays the role of freeing the allocated memory blocks that are actually unused. We assume the garbage collecting policy stop-the-world, meaning that during the memory optimisation time, the customer service is suspended. The aim of the garbage collector is to reduce the memory occupancy of the processes in order to maintain the number i of occupied blocks of memory low, and hence improve the service rate. Observe that, since garbage collectors are able to perform also data compression activity (thus reducing heap-memory fragmentation), it is possible (although unlikely) that at the end of its run the number of used blocks is lower than the number of customers in the system. The garbage collector is activated in two cases:
(a) The system memory is full, i.e., i = B and a customer arrival event occurs;
(b) A timer set up with an exponentially distributed delay expires. The mean duration of these delays is a-1, and we call a the activation rate of the garbage collector. Also in this case, one may assume the activation rate to be function of the occupied blocks of memory, i.e., ai;
The analysis of each memory block is carried out in an exponentially distributed random time with rate Yi, with 1 < i < B. This rate, in general, depends on the memory occupancy, since some swaps may be necessary in case of blocks allocated in the disk. However, the garbage collection is unconditionally interrupted after a random delay f3i, with 1 < i < B. This is done in order to prevent long-lasting blocking in the customer service activity. f3i is called the deactivation rate. For instance, in case of server for graphical interactive applications (such as, on-line games) it may be worth to set up both high activation and deactivation rates, so that the garbage collector is frequently done for short times. On the other hand, a web server has not such a strict requirement.
6. As a final assumption, we consider the case of empty system, i.e., no customer (process) is being processed. In this case the garbage collector can immediately free all the memory blocks.
State of the Model and Transition Diagram. We consider that the garbage collector can be active or suspended. Hence, we specify two possible states for the garbage collector: ON and OFF. When the garbage collector is switched on, all the other activities of the server are blocked, i.e., customers cannot be served. In our model, the state of the system can be completely described by a triplet (c, i, g), where c is the number of customers in the system, i is the number of occupied blocks and g is the state of the garbage collector, e.g. the state (5, 3, ON) means that there are 5 customers in the system, 3 blocks of used memory and that the garbage collector is running. Formally, the state space of the process is
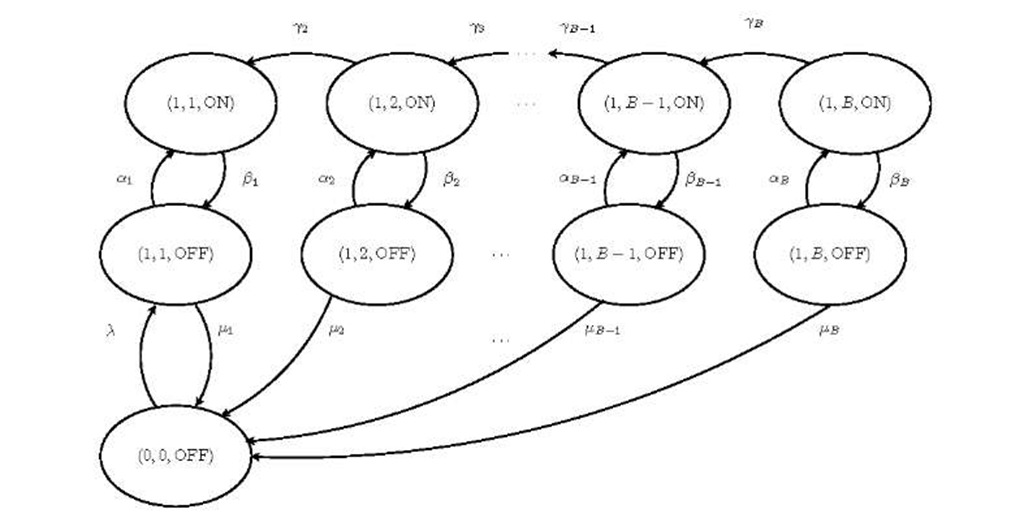
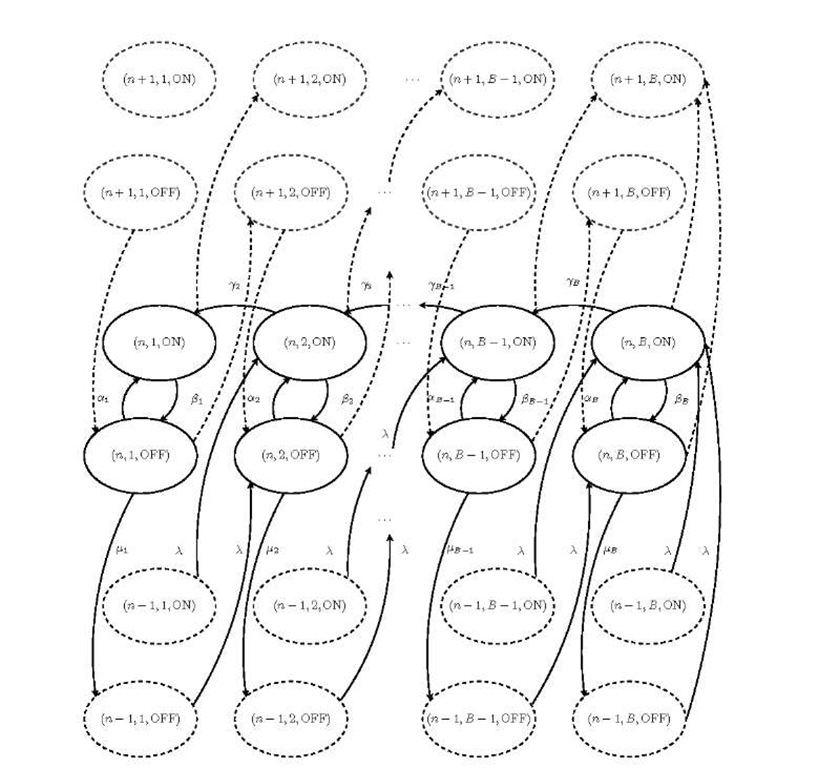
Figure 2 illustrates the structure of the regular portion of the resulting CTMC. We can notice that transitions from or to the state (c, i,g) occurs only with neighbouring states, i.e., states (c’, ii, g’) where
, and have a regular pattern for every number of customers c > 1. This, as shown before, means that this is a QBD process, and that the infinitesimal generator of the Markov process has a regular block structure like the one described in Section 2.2. Moreover, we can assume that the system is initially empty, and that every time the system become empty again, all memory is instantaneously released, i.e., when c = 0 there is only one state (0, 0, OFF) that behaves as shown in Figure 1.
Definition of the Matrix-blocks for the Matrix Geometric Analysis. Given the regular structure depicted above, we can formally define the structure of the blocks which the infinitesimal generator of the underlying CTMC consists of.
Fig. 1. CMTC transitions for the queue with 0 or 1 customer and b = 1. For the sake of clarity, transitions from and to non represented states are omitted.
Fig. 2. The regular blocks of the model for b =1
We use the same block name as those given by Equation (1). Ao, Ai and A2 are matrices of size 2B x 2B, defined as follows:
Here the even rows and columns represent states (c, i, g) where g = ON, i.e., the garbage collector is active, while the odd ones represents states where g = OFF.
Moreover, let B0, B1 and B2 be a column vector of size 2B, a single-component vector and a row vector of size 2B, respectively, defined as follows:
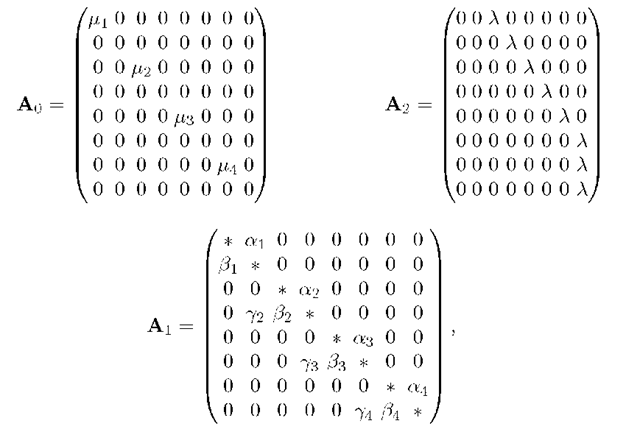
Example 1. Let us consider the case B = 4, then we have:
where diagonal elements, denoted with *, are given by Equation (6).
Analysis. As we pointed out before, the stochastic model has an underlying QBD process, hence the equations and analysis method described in Section 2 can be applied. Specifically, the steady-state probabilities can be computed once Neuts’ matrix R is known and the closed matrix-formula (4) and (5) can be applied. Other interesting performance indices may be computed up to an arbitrary precision, by truncation of the Markov process, e.g., the overhead caused by the garbage collector or the mean time spent after a garbage collector activation. Stability condition can be tested with inequality (3).
We are interested in establishing the activation rate of the garbage collector that minimises the mean response time of the system. We assume that all the other parameters are given and, in particular, that the duration of the garbage collector runs are determined by system requirements, such as avoiding long-lasting stop-the-world phases. As a simplifying hypothesis, let us consider constant rates
and let
be the mean response time of the model as function of a. Hence, we should address the optimisation problem:
i.e., finding the optimum garbage collector activation rate that minimises the mean response time. Since we do not have an analytic expression for function R(a) a numerical approach must be adopted, and an interval inside which the optimum is contained must be found. The following proposition gives this interval.
Proposition 1. If the optimisation problem (7) admits a solution, then the following inequality holds:
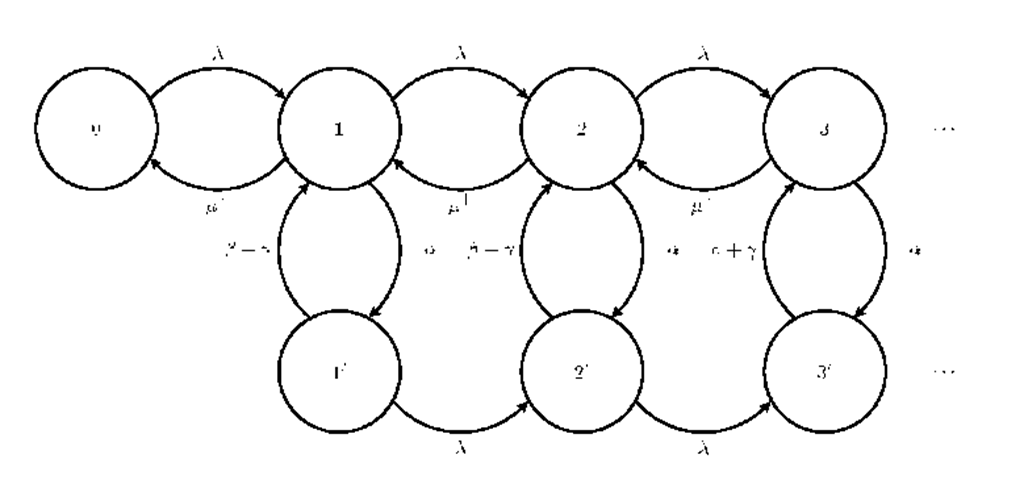
Proof. We aim to find an upper bound a+ for the activation rate. We derive a+ as the stability condition of a queue whose service rate is higher than that of the model we are studying. The fictitious queue, whose underlying stochastic process is depicted in Figure 3, alternates working-phases and idle-phases and has a Pois-son arrival process. The service rate, when in activity, is exponentially distributed with rate
Observe that this service rate is an upper bound of that of the garbage collector queue. We want that the rate at which the fictitious queue enters into an idle state to be an upper bound of the garbage collector activation rate, i.e., we assume it to be a. Finally, we need to find a lower bound for the rate of entering again into an active-state from a idle-state. Observe that, in the GC model the time spent in the collecting phase which starts from i has the distribution of the minimum of the sum of i independent exponential random variables with parameter 7 and the exponential random variable with parameter [. In the average, the time is greater than the minimum of one exponential random variable with rate 7 and one with rate [, i.e., a random variable with rate 7 + [. The fictitious queue is itself a simple QBD process whose stability condition is necessary for the stability of the original queue. The symbolic condition can be easily derived using Inequality (3). Note that, a purely algebraic approach may also be taken to prove that the stability condition of the fictitious queue is necessary for that of the original garbage collector queue. In this case, one first observes that the left-hand-sides of Inequality (3) is A for both queues. For what concerns the right-hand-sides, observe that the easy structure of A0 (in both the queues) and the observation that for large n the probability of observing the garbage collector inactive (odd states) is lower in the original queue than in the fictitious one (which relates the vector na of both the queues), we algebraically obtain the proof. □
Fig. 3. The fictitious model used to prove Equation (8)
Given the interval of search non-linear optimisation problem (7) can be solved, e.g., with a Golden section search or, more practically, with Matlab function fmincon. Observe that, although we have not the proof that the there exists only one minimum, we surely know that if a stability region of the queue exists for a, then there is at least a local minimum. By informal considerations on the model behaviour, and supported by experimental evidences, we also conjecture that the local minimum is unique and hence also an absolute minimum.
