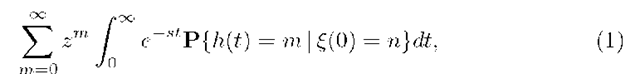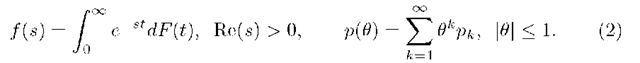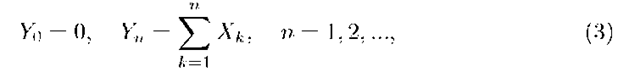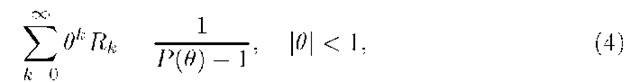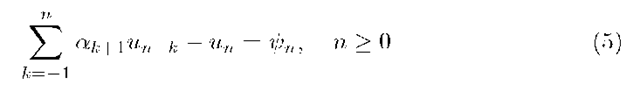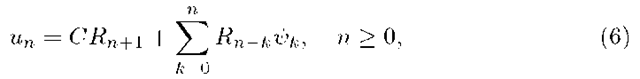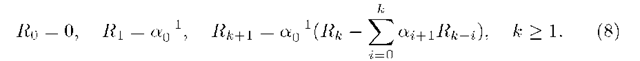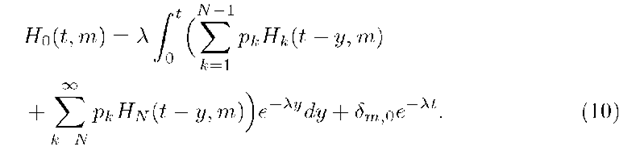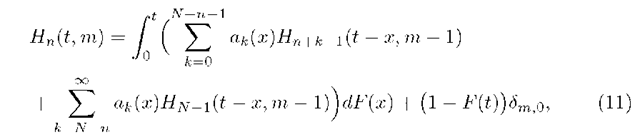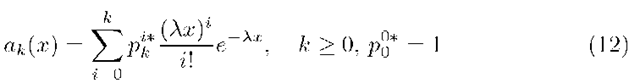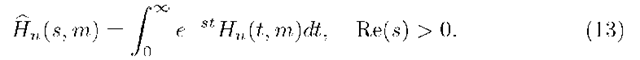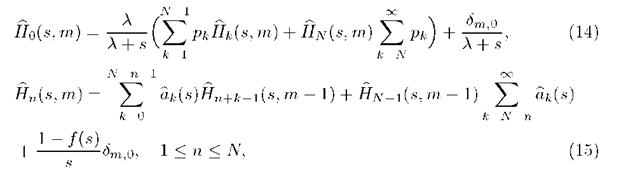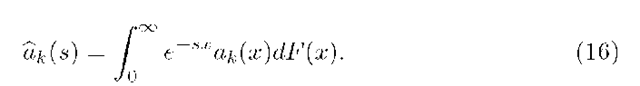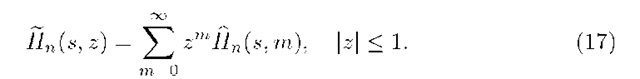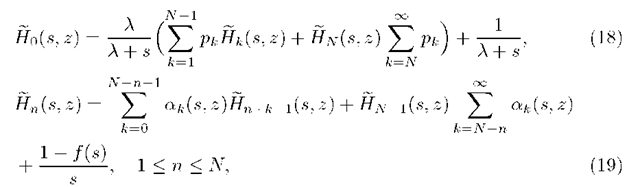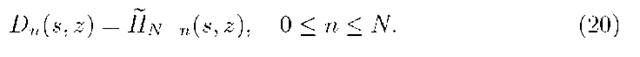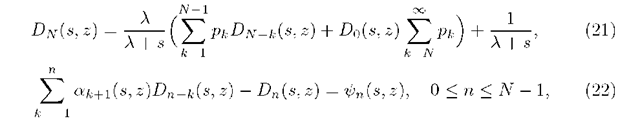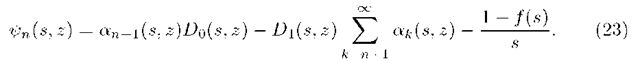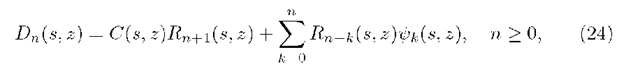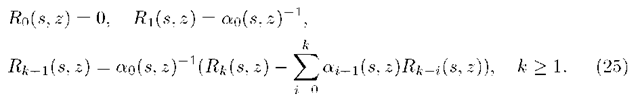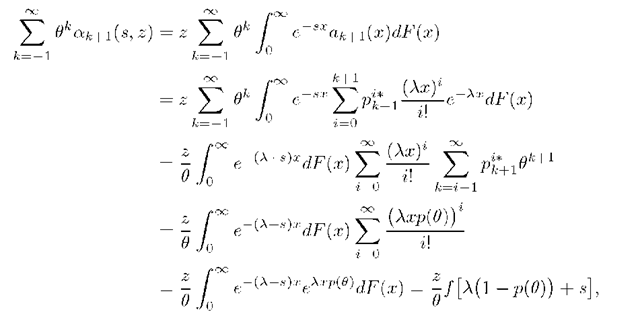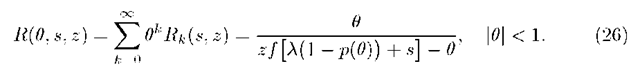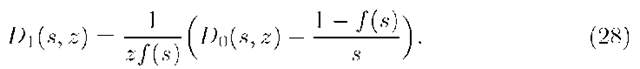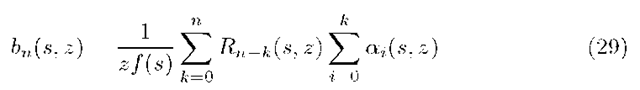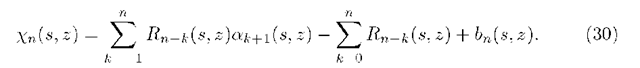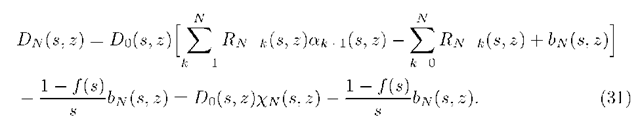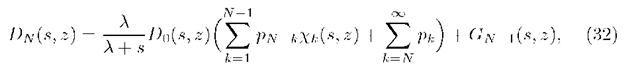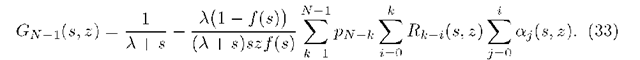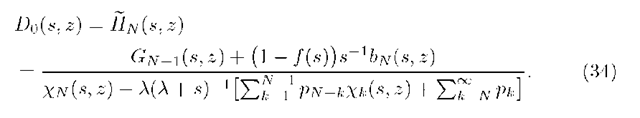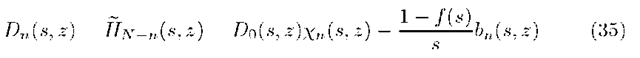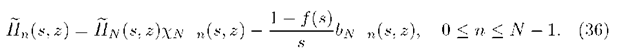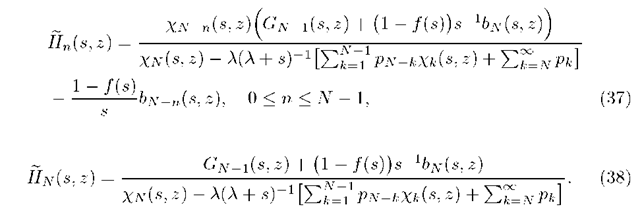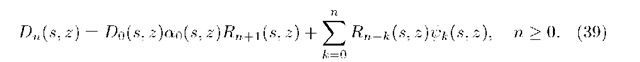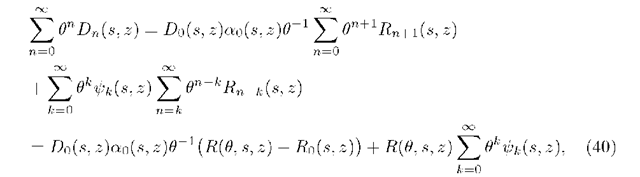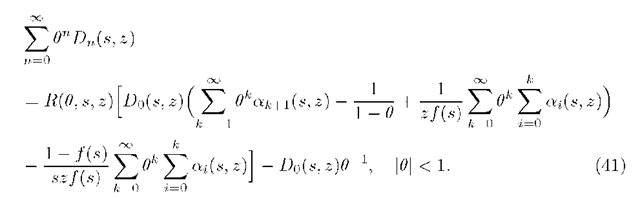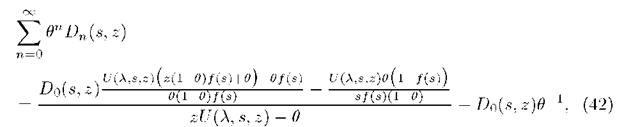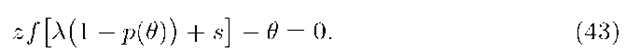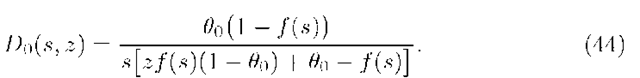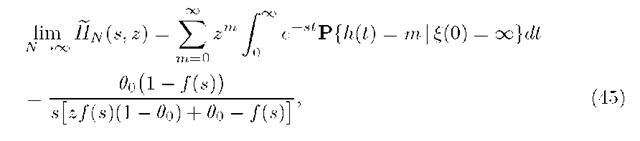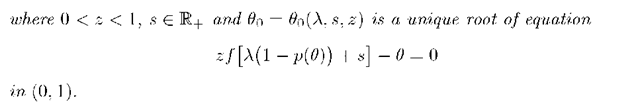Abstract
A finite-buffer queueing system with batch Poisson arrivals is considered. A system of integral equations for the distribution function of the number of customers h(t) served before t, conditioned by the initial state of the system, is built. A compact formula for probability generating function of the Laplace transform of distribution of h(t) is found using the potential technique. From this representation the mean of h(t) can be effectively calculated numerically using one of the inverse Laplace transform approximation algorithms. Moreover a limit behavior of departure process as the buffer size tends to infinity is investigated. Numerical examples are attached as well.
Keywords: Departure process; Finite-buffer queue; Numerical inverse Laplace transform; Poisson arrivals; Potential method.
Introduction
Finite-buffer queueing systems are intensively investigated nowadays due to their applications in modelling of Internet routers. Of special significance is the analysis of systems in transient state i.e. at fixed moment t. We are often interested in the investigation of key system characteristics during a short period of time only since, because of permanent changing of Internet traffic, the notion of "stationary state" in reality does not occur. Besides, especially the analysis of systems with batch arrivals is desired and expected from the practical point of view. In real Internet traffic the incoming packets have different sizes measured in bytes, thus treating a byte as a unit we can consider a stream of different-sized packets as a stream of single one-byte packets arriving in groups of random sizes.
One of the essential characteristics determining the efficiency (the "function") of the service process with respect to the intensity of the arrival stream is departure process h(t), that at any fixed moment t takes on a random value equal to the number of packets completely served before t. In the paper we investigate this characteristic in the MX/G/l/N system with Poisson batch arrivals. The main goal of the analysis is to find an explicit, compact representation for probability generating function of the Laplace transform of the distribution of the departure counting process, conditioned on the number of packets present in the system at t = 0. According to the best knowledge of the author such a result is new in finite-buffer systems analysis. In any case the bibliography on transient departure processes is rather modest. In [6] a steady-state joint density function of k successive departure intervals is derived for the M/G/l/N system. Besides the problem of correlation of such intervals is discussed. Some problems connected with the service process in MX/G/1/N are solved in [2]. In particular, a joint distribution function of the length of the first lost series of batches and the time of the first loss is found. An interesting technique of investigation of finite-buffer systems is developed in [7]. The approach is based on resolvent sequences of the process being the difference of a compound Poisson process and a compound general-type renewal process. An overview of results related to finite-buffer systems with Markovian input streams can be found in [13] and [3]. Transient results for the departure process in the case of the system with batch arrivals and infinite queue can be found in [8] and [9], [10], where additionally multiple and single vacation policies are analyzed.
In the article we use the technique of potential introduced in [11] and developed in [12]. Some details connected with this approach are stated in the next Section 2 where a precise system description is given as well. In Section 3 we obtain the main result i.e. the explicit representation for the expression
where 0 < n < N, t > 0, \z\ < 1, Re(s) > 0, and £(0) denotes the number of packets present in the system at the opening. In Section 4 we derive a limit representation for 2-fold transform of departure process as the buffer size tends to infinity. The last Section 5 contains sample numerical results for the mean of departure process obtained using one of the algorithms for numerical Laplace transform inversion.
System Description and Potential Approach
In this article we consider the MX/G/1/N queueing system in that the incoming batches of packets arrive according to a Poisson process with intensity A and the size of the arriving batch is k with probability
. Packets are served individually with a distribution function F(•). The system capacity is assumed to be N i.e. we have N — 1 places in the buffer queue and one place for service. To complete necessary notation let us put
By pj we denote the jth term of the i-fold convolution of the sequence (pk) with itself. Besides, let 5i}j denotes the Kronecker delta function.
The notion of potential of a random walk continuous from below was introduced in [11] (see also [12]). Here we state only selected elements of potential theory, which will be used later. Originally (see [ll]) the potential is defined as follows. Introduce a discrete-time random walk Yn in the following way:
where Xn are independent and identically distributed random variables with a discrete distribution rk = P{Xn = k}, k = —l, 0, l,…, where r-\ > 0. A sequence
satisfying condition
where
is called a potential of random walk Yn or, simply, a potential of the sequence (rk). Thus, the potential (Rk) of the sequence (rk) is such a sequence the generating function of which can be written down using the generating function of the sequence (rk) as in (4).
In the analysis of finite-buffer queue characteristics the following property of sequence
can be applied ([ll]):
Theorem 1. Introduce two number sequences
with the assumption
The general solution of the following boundary problem:
can be written in the form
where C is a constant independent on n and Rk is the potential connected with sequence (an) i.e.
and, besides, Rk can be found in the following recurrent way:
Theorem l is essential for the analysis. Its importance lies in the fact that it allows to write down in a compact form the general solution of a specific-type system of equations, which appears in the transient investigation of finite-buffer queues with Poisson arrivals. A detailed proof of this theorem can be found in [ll]. Theorem l, perhaps in a slightly different form, was applied e.g. in [2], [3] and [4].
System of Integral Equations for Departure Process
In this section we will write the system of integral equations for conditional distributions of departure process h(t) and obtain the explicit formula for probability generating function of Laplace transform of probabilities P{h(t) = m \ £(0) = n}. Introduce the following notation:
Note that the following equation is true:
Indeed, if the system is initially empty the first summand in (10) relates to the situation in that the first group of packets enters before t. The number of packets in the system after the first arrival differs in dependence on the first group size, and for groups of size k > N reaches the maximum level N. In the second summand the first arrival epoch is after t, so h(t) = m if and only if m = 0.
As it is well known (see e.g. [5]) departure epochs are Markov moments in the queueing system with Poisson arrivals. Hence the formula of total probability used with respect to the first (after t = 0) departure epoch x > 0 leads to the following system of integral equations:
where 1 < n < N, and
denotes the probability that exactly k customers enters to the system before time x.
The interpretation of both sides of (11) is similar to that in the case of (10). The first summand in the integral on the right in (11) denotes the situation in that the first departure epoch occurs at time x < t. If exactly k packets have entered until x then, since x is a Markov moment, we can consider x as the initial moment of the system starting with n + k — 1 packets (k arrivals till x and one departure), and the event {h(t) = m} will become {h(t — x) = m — l}. In the second summand in the integral on the right in (ll) the number of packets which arrive before the first departure epoch x equals at least N — n, so N — n packets are enqueued only (to saturate the buffer), the remaining ones are lost. Thus, after the first departure epoch the number of packets in the system is N — l. The last summand on the right side in (ll) describes the situation in that the first departure occurs after t.
Introduce the Laplace transform of Hn(t,m) with respect to argument t as follows:
Now (l0)-(ll) lead to
where
To eliminate dependence on m let us now introduce a generating function of Hn(s, m) of the form
Equations (l4)-(l5) will take now the form
where ak(s,z) = zak(s).
Now let us make the following substitution:
Introducing (20) into (18)-(19) gives
where
Note that the system (22) has the form stated in (5). The only difference is in that functions depend on arguments s and z. The general solution of (22) can be written in the form (compare (6))
where (see (8))
Of course, taking into consideration that
we get from (7)
Now we must find the representation for C(s,z). Substituting n = 0 to (24) leads to
Taking n = 0 in (22) we obtain
that, since
Introduce the following functionals:
and
Now, substituting n = N to (24) and using (23), (27) and (28) we get
Similarly, introducing (23), (24), (27) and (28) into (2l), after a little laborious calculations we obtain
where
Comparing the right sides of (3l) and (32) we eliminate D0(s, z) as follows:
Now from (24) (applying (29) and (30)) we get for 1 < n < N
and hence, after operation on indexes, we obtain
Collecting formulae (34) and (36) we can state the following main theorem:
Theorem 2. For any \z\ < 1 and Re(s) > 0 the following representations hold true:
Limit Theorem
This section is devoted to the limit behavior of 2-fold transform of departure process in the case of infinitely increasing buffer size i.e. as N ^ m. We start with the formula (24). Taking into consideration (27) we have
Multiplying (39) by 0n and, under the assumption
taking a sum over n from 0 to to we obtain, along the way applying identity (26)
where \0\ < 1. Using in (40) representations (23) and (28) we derive
Taking into consideration the formula (26) we get from (4l) for \0\ < l
where we denote
Let us take into consideration the following equation:
Treat the left side as a function Q of variable 0, for fixed 0 < z < l and s such that Im(s) = 0, Re(s) > 0. Substituting 0 = 0 we have
and similarly taking 0 = l we get Q(l) = zf(s) — l <z — l < 0. Since Q’(0) =
thus there exists a unique root
of (43) between 0 and l. The series on the left side of (42) is convergent in particular for 0 < 0 < l, hence the numerator of the expression on the right side of (42) should be 0 at 00.
Substituting 00 to the numerator of the expression on the right side of (42) we eliminate D0(s,z) as follows:
Since for
we have
we can now formulate the following limit theorem:
Theorem 3. For conditional 2-fold transform of departure process as the initial number of packets tends to infinity the following limit representation holds:
