Abstract
The high-level contribution of this paper is to establish benchmarks for the minimum hop count per source-receiver path and the minimum number of edges per tree for multicast routing in mobile ad hoc networks (MANETs) and explore the tradeoffs between these two routing strategies with respect to hop count, number of edges and lifetime per multicast tree. Accordingly, we consider two categories of algorithms – Breadth First Search (for minimum hop trees) and minimum Steiner tree heuristic (for minimum edge trees). Extensive simulations of these two algorithms on centralized snapshots of the MANET topology, sampled for every 0.25 seconds, have been conducted for 1000 seconds under two different conditions of network density and three different multicast group sizes. Simulation results illustrate that minimum edge trees have 20-160% larger lifetime than the minimum hop trees. The tradeoff is that the minimum edge trees have 20-100% larger hop count per source-receiver path compared to the minimum hop trees. Similarly, the minimum hop trees have 13-35% more edges than the minimum edge trees.
Keywords: Minimum Hop, Minimum Edge, Multicast Routing, Mobile Ad hoc Networks, Simulations, Steiner Trees.
Introduction
A mobile ad hoc network (MANET) is a dynamic distributed system of wireless nodes that move independent of each other in an autonomous fashion. The network bandwidth is limited and the medium is shared. As a result, transmissions are prone to interference and collisions. The battery power of the nodes is constrained and hence nodes operate with a limited transmission range, often leading to multi-hop routes between any pair of nodes in the network. Multicasting in wireless ad hoc networks has numerous applications in collaborative and distributed computing. In this paper, we adopt the Least Overhead Routing Approach of using a chosen multicast tree as long as it exists and determining a new tree only when the currently used one breaks.
Not much work has been done towards the evaluation of MANET multicast routing from a theoretical point of view with respect to metrics such as the hop count per source-receiver path and the number of edges per multicast tree and their impact on the lifetime per multicast tree. These two theoretical metrics significantly contribute and influence the more practically measured performance metrics such as the energy consumption, end-to-end delay per packet, routing overhead and etc. that have been often used to evaluate and compare the different MANET multicast routing protocols in the literature. Hence, we take a different approach in this paper. We study MANET multicast routing using the theoretical algorithms that would yield the benchmarks (i.e., optimum values) for the above two metrics – the Breadth First Search (BFS) algorithm [3] for the minimum hop count per source-receiver path and the minimum Steiner tree heuristic [4] for the minimum number of edges.
Our simulation methodology is outlined as follows: Using the mobility profiles of the nodes gathered offline from a discrete-event simulator (ns-2 [6]), we will generate snapshots of the MANET topology, referred to as Static Graphs [7], periodically for every fixed time instant. For simulations with a particular algorithm, if a multicast tree is not known for a particular time instant, we will run the algorithm on the static graph in a centralized fashion and adopt the LORA strategy of using this multicast tree as long as it exists for the subsequent static graphs. If the tree no longer exists after a certain time instant, the multicast algorithm is again run to determine a new tree. This procedure is repeated for the entire simulation time. Depending on the algorithm used, the sequence of multicast trees generated either have the minimum hop count per source-receiver path or the minimum number of edges. Our hypothesis is that the multicast trees, determined to optimize one of the two theoretical metrics, would be sub-optimal with respect to the other metric. Through extensive simulation analysis, we confirm our hypothesis to be true and we explain in detail the performance tradeoffs associated with the two metrics.
The rest of the paper is organized as follows: Section 2 discusses the existing related work on MANET multicast routing. Section 3 introduces the notion of a Static Graph and reviews the BFS algorithm for minimum hop path trees and Kou et al.’s heuristic for minimum edge Steiner trees. Section 4 presents the simulation results for the benchmark values of the two theoretical metrics, explores the tradeoffs between these metrics and their impact on the lifetime per multicast tree. Section 5 concludes the paper. We use the terms ‘vertex’ and ‘node’, ‘algorithm’ and ‘heuristic’, ‘destination’ and ‘receiver’ are used interchangeably. They mean the same.
Existing Related Work
Several MANET multicast routing protocols have been proposed in the literature [1][2]. They are mainly classified as: tree-based and mesh-based protocols. In tree-based protocols, only one route exists between a source and a destination and hence these protocols are efficient in terms of the number of link transmissions. The tree-based protocols can be further divided into two types: source tree-based and shared tree-based. In source tree-based multicast protocols, the tree is rooted at the source. In shared tree-based multicast protocols, the tree is rooted at a core node and all communication between the multicast source and the receiver nodes is through the core node. Even though shared tree-based multicast protocols are more scalable with respect to the number of sources, these protocols suffer under a single point of failure, the core node. On the other hand, source tree-based protocols are more efficient in terms of traffic distribution. In mesh-based multicast protocols, multiple routes exist between a source and each of the receivers of the multicast group. A receiver node receives several copies of the data packets, one copy through each of the multiple paths. Mesh-based protocols provide robustness at the expense of a larger number of link transmissions leading to inefficient bandwidth usage. Considering all the pros and cons of these different classes of multicast routing in MANETs, we feel the source tree-based multicast routing protocols are more efficient in terms of traffic distribution and link usage. Hence, all of our work in this research will be in the category of on-demand source tree-based multicast routing.
Some of the recent performance comparison studies on MANET multicast routing protocols reported in the literature are as follows: In [9], the authors compare the performance of the tree-based MAODV and mesh-based ODMRP protocols with respect to the packet delivery ratio and latency. In [10], the authors propose a stability-based multicast mesh protocol and compare its performance with ODMRP. [11], the authors compare a dominating set-induced mesh based multicast routing protocol for efficient flooding and control overhead and compare the protocol’s performance with that of MAODV and ODMRP. In [12], the authors explore the use of genetic algorithms to optimize the performance the performance of tree and mesh based MANET multicast protocols with respect to packet delivery and control overhead. The impact of route selection metrics such as hop count and link lifetime on the performance of on-demand mesh-based multicast ad hoc routing protocols has been examined in [13]. In [14], the author has proposed non-receiver aware and receiver-aware (depending on whether the nodes in the network are aware of the multicast group or not) extensions to the Location Prediction Based Routing (LPBR) protocol to simultaneously minimize the edge count, hop count and number of multicast tree discoveries. An agent-based multicast routing scheme (ABMRS) that uses a set of static and mobile agents for network and multicast initiation and management has been proposed in [15] and compared with MAODV. A zone-based scalable and robust location aware multicast algorithm (SRLAMA) has also been recently proposed for MANETs [16].
Review of the Algorithms Used for Multicast Simulations
In this section, we describe the two theoretical algorithms (BFS and Minimum Steiner tree heuristic) used in this paper. We implement these theoretical algorithms to simulate multicasting on a sequence of static graphs over the duration of the multicast session. A static graph is a snapshot of the MANET topology at a particular time instant. Using the mobility profiles of the nodes generated offline from ns-2, we will be able to determine the locations of a node at any particular time instant. A static graph G(t) = (V, E) generated for a particular time instant t, comprises of all the nodes in the network as the vertex set V; there exists an edge (u, v)e E, if and only if, the Euclidean distance between the two end vertices u and ve V, is less than or equal to the transmission range of the nodes in the network. All the edges in E are of unit weight. We assume a homogeneous network of nodes and all nodes operate at an identical and fixed transmission range.
Breadth First Search (BFS) Algorithm
The BFS algorithm (pseudo code in Figure 1) has been traditionally used to check the connectivity of a network graph. When we start the BFS algorithm on a randomly chosen node, we should be able to visit all the vertices in the graph, if the graph is connected. BFS returns a tree rooted at the chosen start node; when we visit a vertex v for the first time in our BFS algorithm, the vertex u through which we visit v is considered as the predecessor node of v in the tree. Every vertex in the BFS tree, other than the root node, has exactly one predecessor node. When we run BFS on a static graph with unit edge weights, we will be basically obtaining a minimum hop multicast tree such that every node in the graph is connected to the root node (the multicast source node) of the tree on a path with the theoretically minimum hop count. If MG C V represents the multicast group of receiver nodes and a source node we start BFS at s and visit all the vertices in the network graph. Once we obtain a BFS tree rooted at s, we trace back from every receiver de MG and determine the minimum hop s-d path. The minimum hop multicast tree is an aggregate of all these minimum hop paths connecting the source s to receiver d in the multicast group.
Fig. 1. Pseudo Code for Breadth First Search (BFS)
Minimum Edge Multicast Steiner Tree
Given a static graph, G = (V, E), where V is the set of vertices, E is the set of edges and a subset of vertices (called the multicast group or Steiner points) MG c V, the multicast Steiner tree is the tree with the least number of edges required to connect all the vertices in MG. Unfortunately, the problem of determining a minimum edge
Steiner tree in an undirected graph like that of the static graph is NP-complete. Efficient heuristics (e.g., [4]) have been proposed in the literature to approximate a minimum Steiner tree. In this paper, we use the Kou et al’s [4] well-known O(iVIIMGI2) heuristic (IVI is the number of nodes in the network graph and IMGI is the size of the multicast group comprising of the source nodes and the receiver nodes) to approximate the minimum edge Steiner tree in graphs representing snapshots of the network topology. An MG-Steiner-tree is referred to as the minimum edge Steiner tree connecting the set of nodes in the multicast group MG C V. In unit disk graphs such as the static graphs used in our research and in [5], Step 5 of the heuristic is not needed and the minimal spanning tree TMG obtained at the end of Step 4 could be considered as the minimum edge Steiner tree. Figure 2 outlines the heuristic.
Input: A Static Graph G = (V, E) Multicast Group MG c V Output: A MG-Steiner-tree for the set MG c V Begin Kou et al Heuristic (G, MG)
Step 1: Construct a complete undirected weighted graph GC = (MG, EC) from G and MG where V (vi, j e EC, vi and Vj are in MG, and the weight of edge (vi, Vj) is the length of the shortest path from vi to vj in G.
Step 2: Find the minimum weight spanning tree TC in GC (If more than one minimal spanning tree exists, pick an arbitrary one).
Step 3: Construct the sub graph GMG of G, by replacing each edge in TC with the corresponding shortest path from G (If there is more than one shortest path between two given vertices, pick an arbitrary one).
Step 4: Find the minimal spanning tree TMG in Gmg (If more than one minimal spanning tree exists, pick an arbitrary one). Note that each edge in GMG has weight 1.
Simulations
The simulations have been conducted in a discrete-event simulator implemented by the author in Java. The two multicast algorithms have been implemented in a centralized fashion. We generate the static graphs by taking snapshots of the network topology, periodically for every 0.25 seconds, and run the two multicast algorithms. The simulation time is 1000 seconds. We consider a square network of dimensions 1000m x 1000m. The transmission range of the nodes is 250m. The network density is varied by performing the simulations with 50 nodes (low density) and 100 nodes (high density). We assume there is only one source for the multicast group and three different values for the number of receivers per multicast group are considered: 3 (small), 10 (moderate) and 18 (large). A multicast group comprises of a source node and a list of receiver nodes, the size of which is mentioned above.
The node mobility model used is the Random Waypoint model [8]. Each node starts moving from an arbitrary location (i.e., waypoint) at a speed uniformly distributed in the range [vmin, ..., vmax]. Once the destination is reached, the node may stop there for a certain time called the pause time and then continue to move to a new waypoint by choosing a different target location and a different velocity. A mobility trace file generated for a particular vmax value over the duration of the simulation time is the congregate of the location, velocity and time information of all the waypoints for every node in the network. In this paper, we set vmin = 0. The vmax values used are 5 m/s (low mobility), 25 m/s (moderate mobility) and 50 m/s (high mobility). The pause time is 0 seconds.
The performance metrics measured are as follows. Each performance metric illustrated in Figures 3 through 6 is measured using 5 different lists of receiver nodes for the same size and the multicast algorithm is run on five different mobility trace files generated for a particular value of vmax.
(i) Number of links per tree: This metric refers to the total number of links in the entire multicast tree, time-averaged over the duration of the multicast session. For example, a multicast session uses two trees, one tree with 10 links for 3 seconds and another tree with 15 links for 6 seconds, then the time-averaged value for the number of links per tree for the 9-second duration of the multicast session is (10*3 + 15*6)/(3 + 6) = 13.3 and not 12.5.
(ii) Number of hops per receiver: We measure the number of hops in the paths from the source to each receiver of the multicast group and average it for the duration of the multicast session. This metric is also a time-averaged value of the number of hops from a multicast source to a receiver and then averaged over all the receivers of a multicast session.
(iii) Lifetime per Multicast Tree: Whenever a link break occurs in a multicast tree, we establish a new multicast tree. The lifetime per multicast tree is the average of the time between successive multicast tree discoveries for a particular routing protocol or algorithm, over the duration of the multicast session. The larger the value of the lifetime per multicast tree, the lower the number of multicast tree transitions or discoveries needed.
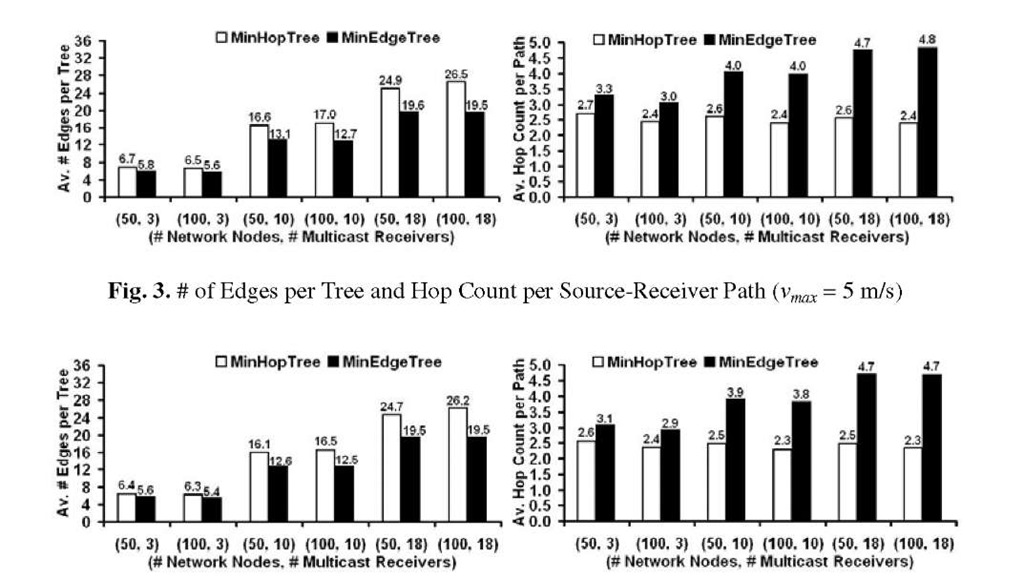
Number of Edges per Tree and Hop Count per Source-Receiver Path
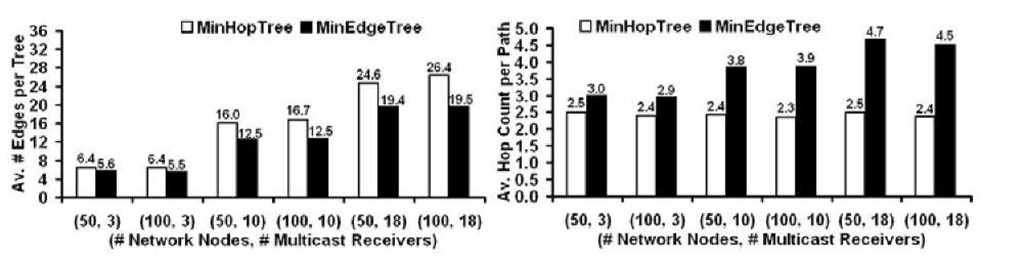
As expected, the minimum-edge based Steiner trees incurred the smallest number of edges per multicast trees. On average, the number of edges per minimum hop tree is 13-35% more than those incurred with the minimum edge tree. With an objective to optimize the hop count, minimum hop based multicast trees select edges that could constitute a minimum hop path, but with a higher probability of failure in the immediate future. The physical Euclidean distance between the constituent nodes of an edge on a minimum hop path is close to the transmission range of the nodes at the time of tree formation itself. For a given network density, as we increase the number of receivers per multicast group from 3 to 18, the average number of edges per multicast tree increased by a factor of 3 to 4. For the minimum hop and minimum edge trees, for a given level of node mobility and number of receivers per multicast group, as we increase the network density, the number of edges per multicast tree either remains the same or even slightly decreases.
As expected, the minimum hop multicast trees incurred the lowest hop count per source-receiver path. The larger hop count per source-receiver path for minimum edge trees could be attributed to a relatively lower number of edges compared to the minimum hop trees. As we connect the source node to the multicast receivers with the lowest possible number of edges, the number of hops between the source node and to each of the receiver nodes increases. This is the tradeoff between the objectives of minimizing the number of edges per multicast tree and the hop count per individual source-receiver paths in the multicast tree.
Fig. 4. # of Edges per Tree and Hop Count per Source-Receiver Path (v = 25 m/s)
Fig. 5. # of Edges per Tree and Hop Count per Source-Receiver Path (v = 50 m/s)
For both minimum hop and minimum edge multicast trees, for a given network density and number of receivers per multicast group, there is appreciably no impact of the maximum node velocity on the average number of edges per tree as well as the hop count per source-receiver path. For a given level of node mobility (i.e., maximum node velocity) and network density, as we increase the number of receivers per multicast group, the average hop count per source-receiver path for minimum hop trees decreases. On the other hand, the average hop count per source-receiver path for minimum edge trees increases. This could be attributed to the relatively fewer number of edges in the minimum edge trees compared to those incurred by the minimum hop trees. The relatively more edges in minimum hop trees at larger number of receivers per multicast group results in lower hops count per source-receiver path. The average number of edges per minimum hop tree for a network of 50 nodes and 3 receivers per multicast group is about 1 edge more than those incurred by the minimum edge trees; on the other hand, the average number of edges per minimum hop tree for a network of 50 nodes and 18 receivers per multicast group is about 7 edges more than the minimum. Similar observations could be made for network of 100 nodes.
When compared to the average hop count per source-receiver path incurred by minimum hop trees, the average hop count per source-receiver path for minimum edge trees is 20% (for smaller number of receivers per multicast group) to 100% (for larger number of receivers per multicast group) more. Note that with increase in the network density and/or the number of receivers per multicast group, the trend of the hop counts per source-receiver path for minimum hop trees is to decrease; whereas, the trend of the hop count per source-receiver path for minimum edge trees is to increase. The hop count per source-receiver path for minimum hop trees decreases by at most 14% and 30% respectively; whereas, the hop count per source-receiver path for minimum edge trees increases by at most 47%.
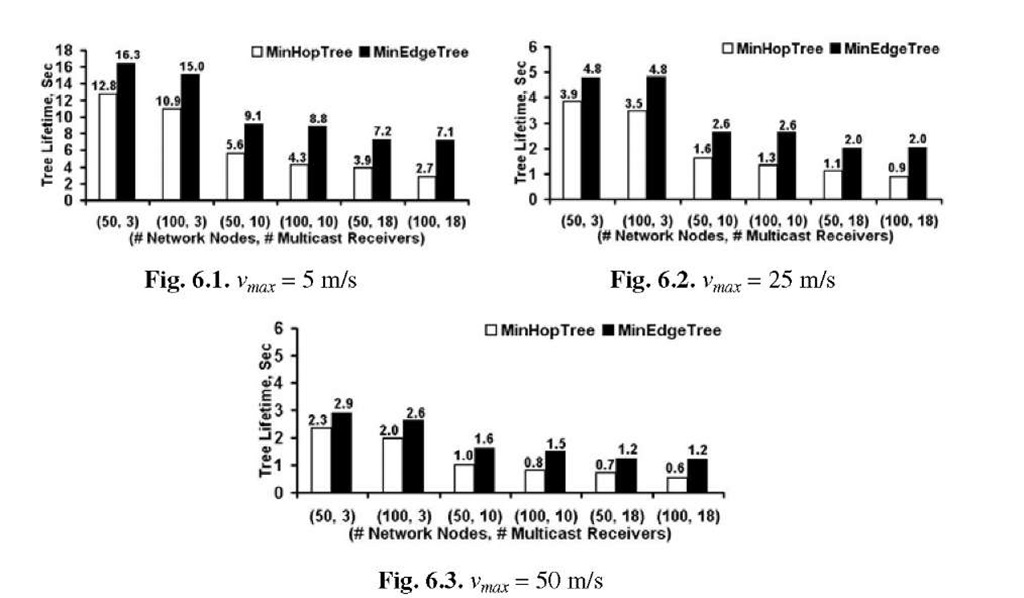
Lifetime per Multicast Tree
The minimum edge multicast trees had a relatively longer lifetime compared to the minimum hop multicast trees. This could be attributed to (i) the increased number of edges (refer to Section 4.1 for more on this observation) in a minimum hop multicast tree; (ii) the physical Euclidean distance between the constituent nodes of an edge on a minimum hop path is close to the transmission range of the nodes at the time of tree formation itself. Thus, the probability of an edge failure is quite high at the time of formation of the tree; (iii) the edges of a tree are also independent from each other. All these three factors play a significant role in the relatively lower lifetime per minimum hop multicast tree.
For both the multicast algorithms, for a fixed network density, as the number of receivers per multicast group is increased, the lifetime per multicast tree decreases moderately at low node mobility and decreases drastically (as large as one-half to one-third of the value at smaller number of receivers per group) at moderate and high node mobility scenarios. This could be attributed to the difficulty in finding a tree that would keep the source node connected to the receivers of the multicast group for a longer time, with increase in node mobility and/or the number of receivers per multicast group. For a given number of receivers per multicast group and node mobility, the lifetime per minimum hop trees and minimum edge trees slightly decreases as we double the network density. The decrease is more predominant for minimum hop trees and this could be attributed to the relatively unstable minimum hop paths in high density networks.
Fig. 6. Lifetime of Minimum Hop Tree vs. Minimum Edge Tree
For a given level of node mobility, the lifetime per minimum edge tree is 23% (low density) to 38% (high density); 61% (low density) to 107% (high density) and 76% (low density) to 160% (high density) larger than the lifetime per minimum hop tree for small, moderate and larger number of receivers per multicast group respectively. For both minimum hop and minimum edge trees, for a given network density and number of receivers per group, as we increase the maximum node velocity to 25 m/s and 50 m/s, the lifetime per tree reduces by 1/3rd to 1/6th of their value at a maximum node velocity of 5 m/s.
Conclusions
We have described the algorithms that can be used to obtain benchmarks for the minimum hop count per source-receiver path and minimum number of edges per tree for multicast routing in mobile ad hoc networks. Simulations have been conducted to obtain such benchmarks for different conditions of network density, node mobility and number of receivers per multicast group. The minimum hop based multicast trees have a larger number of edges than the theoretical minimum – the minimum hop trees are unstable and their lifetime decreases with increase in the number of edges. This could be attributed to the instantaneous decision taken by the minimum hop path algorithm to select a tree without any consideration for the number of edges and their lifetime. The minimum edge trees have a relatively larger hop count per source-receiver path and the hop count per path increases with the number of receivers per multicast group. The relatively fewer edges in the minimum edge tree results in a relatively larger lifetime compared to the minimum hop trees, as each edge in these two trees are independent. The simulation results thus indicate a complex tradeoff between the hop count per source-receiver paths and number of edges per tree vis-avis their impact on the lifetime per tree for multicast routing.