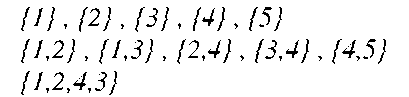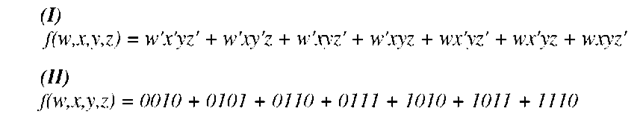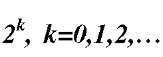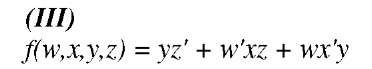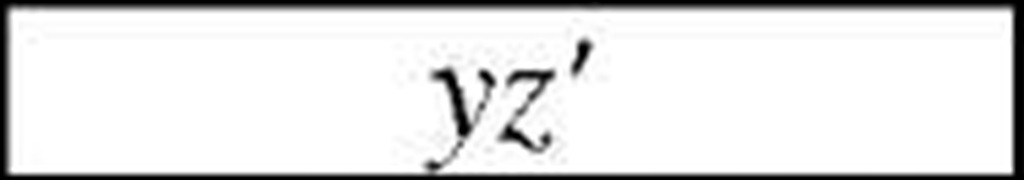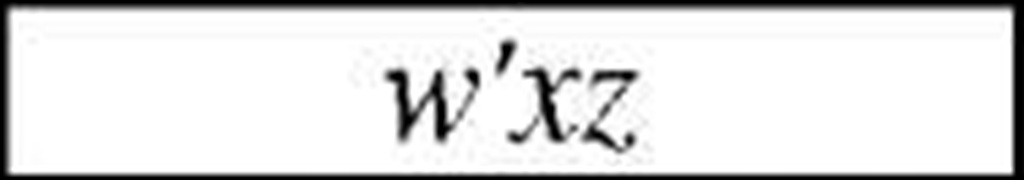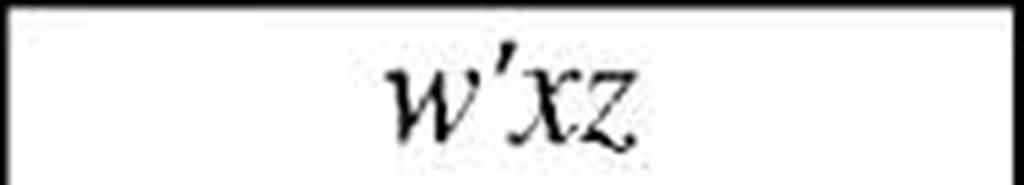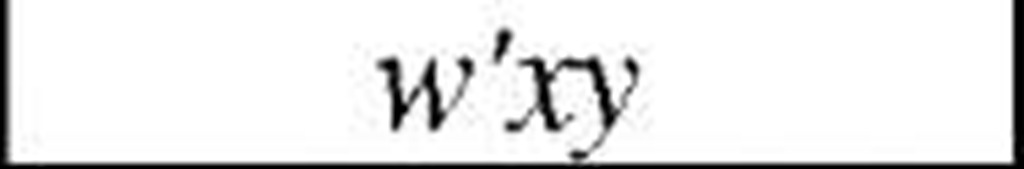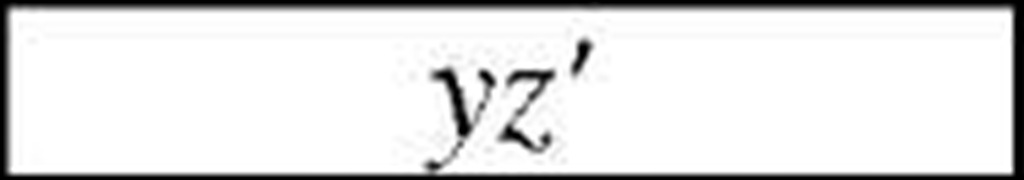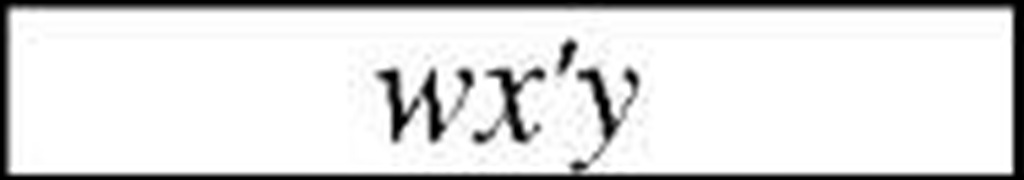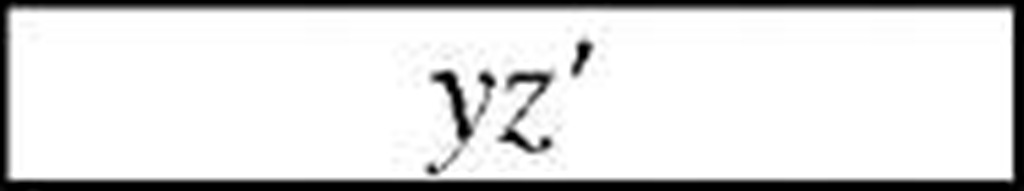Abstract
In this paper, we intend to introduce a heuristic algorithm to apply maximum minimization to Boolean functions with normal SOP form. To implement the proposed algorithm, we use the graph data structure and define the adjacencies. Also, we demonstrate some conditions to achieve the maximum minimization. Through this paper, the problem of shared vertices in more than one adjacency is talked, and the solution is presented. Also, don’t-care statements are considered and the way of behaving with them is explained. Karnaugh map is used to clarify the matter.
Keywords: Minimization of Boolean functions, SOP form, Don’t-care statements, Graph data structure.
Introduction
Minimization of Boolean functions is one of the basic operations in Boolean algebra. This is also useful in digital circuits design, and it was been regarded to decrease the price of manufactured circuits by removing extra gates [1,13,14,20]. In this paper, we present an algorithm to minimize the Boolean functions extremely. We use the graph data structure to implement this algorithm.
In second part which is entitled as "Graph data structure and agreements", the structure of proposed graph and its objects and methods will be talked. In addition, some agreements are presented which are considered during this paper. In third part that is named "SOP functions and graph", the relationship between SOP functions and graph data structure is objected. Furthermore, the conditions of minimization of function by proposed graph are demonstrated. In "Minimization algorithm", that is forth part of this paper, the algorithm of minimization and its description is presented. Eventually, "conclusion" is places as fifth part.
Related Works
Before it, many methods and algorithms was introduced for minimizing a Boolean function. For example, "A Heuristic Method of Two-Level Logic Synthesis" can be pointed out, which uses the weight of cubes to minimize DSOP functions [2].
One important research which is closely related to ours is "Factoring Boolean functions using graph partitioning", which uses graphs also. Central to this approach is to combine the graph partitioning with the use of special classes of Boolean functions, such as read-once functions, to devise new combinatorial algorithms for logic minimization. This method is a generalization of techniques for the so called read-once functions, a special family of monotone Boolean functions, also known as non-repeatable tree (NRT) functions. In this study, authors obtain better results than algebraic factoring in most test cases and very competitive results with Boolean factoring with less computation time [3].
Generally, there are many methods for minimizing Boolean functions. Here we are going to present a new algorithm that uses graph data structure to do the minimization.
Graph Data Structure and Agreements
First time, graph was been used for solving the classic problem of Konigsberg bridges by Leonhard Euler in 1736. After that, graph came into mathematics world [4].
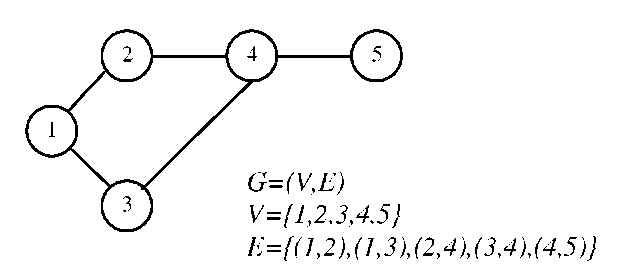
A graph is constructed of two sets, V (vertices) and E (Edges) [18,21]. For example, look at Fig.1.
Fig. 1. A simple example of graph
A path in graph is a set of vertices we should cross to get to a special vertex. If the initial and final vertices are the same, this path is called cycle, and if all the edges in a cycle are met just one time, it is called a simple cycle [5,6,7].
According to these definitions, there is one simple cycle in Fig.1, which is {1,2,4,3}. Here, we make two agreements and describe the reason in third part of paper.
Agreement1: Each vertex makes a simple cycle by itself.
Agreement2: A couple of adjacent vertices make a simple cycle. (Adjacent vertices are those which are related by an edge.)
According to these agreements, the simple cycles for Fig.1 are like below:
Now, we can implement the class of proposed graph data structure. This class contains some objects to store V and E, and also some methods to create and remove vertices and edges [4,8,9,16,18].
The most important method in this class is list Cycles(Vertex V). This method returns the list of all simple cycles that begin with V,-. Also, it should return the number of non-don’t-care vertices in each cycle which is called Wnd (Weight of non-don’t-care vertices). It is a metric to choose the best adjacency for the vertex. Don’t-cares and the usage of Wnd is covered during the next section.
In addition, another method is defined to return the number of all adjacent vertices of V,, too.
SOP Functions and Graph
Boolean functions are used for indicating the performance of combinational two-level circuits with AND – OR gatesThese functions could be shown in normal SOP (Sum Of Products) or POS forms [10,11,17]. We aren’t going to talk about algebraic concepts or the way of generating SOP or POS forms. Just propose that we have a SOP function which should be minimized.
There are different ways to minimize SOP functions. One is using the algebraic rules, which is hard and confusing for large functions with many variables. Another is using Karnaugh map. It could be used for functions with 2 to 6 variables, by drawing the map of adjacency. In fact, Karnaugh map is an illustrative form of truth table. It puts the adjacent statements near each other and provides the opportunity of selecting appropriate adjacency. Fig.2 shows the Karnaugh map for 4-variables Boolean functions. In this map, different states of variables are showed by 0 and 1 [12].
|
0000 |
0001 |
0011 |
0010 |
|
0100 |
0101 |
0111 |
0110 |
|
1100 |
1101 |
1111 |
1110 |
|
1000 |
1001 |
1011 |
1010 |
Fig. 2. Karnaugh map for 4-variables Boolean functions
It is seen that each two adjacent cells has one different bit. In other word, the XOR of two adjacent cells equals 2r, r=0,1,2,….
Consider that function (I) should be minimized by this map. By replacing the variables with 0 and 1 (function (II)), its Karnaugh map will be as Fig.3.
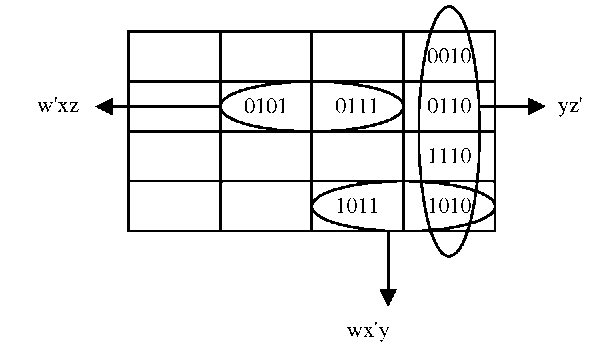
Fig. 3. Karnaugh map for function (I) with appropriate adjacencies
In Fig.3, appropriate adjacencies are selected, and minimization operation – which is remaining similar bits and removing the others [15] – is done. Essential condition to choose an appropriate adjacency is defined as (*).
The number of cells in an adjacency should be equal to similar bits equal to k.
and no
Another point which should be regarded is that always the biggest adjacencies that contain more cells should be selected, in order to make the function more minimized, by reducing more different bits [1,12]. Also, it should be paid attention that in functions with complete statements – where all statements are present – minimized function equals to 1.
It is seen that minimized function (I) will be like function (III).
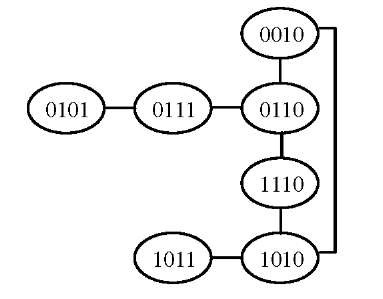
Suppose that fv is a desire Boolean function. It could be adapted to graph data structure, if for each statement in it, create a vertex and show adjacencies by edges. For example, Fig.4 shows the graph of function (I).
Fig. 4. Graph of function (I)
To minimize the function of this graph, first the biggest appropriate adjacencies should be found for each vertex. It has to be done regarding agreements 1 & 2. Now, you can find out the reason of making these agreements. Minimization is operated according to the adjacencies (not vertices), so for each alone vertex, an adjacency should be considered. For two adjacent vertices it has to be done, too. In mathematical definition of simple cycles in no directed graphs, simple cycles with less than 3 vertices are not defined [3,6].
Regarding condition (*), Table.1 shows the biggest simple cycles in graph of Fig.4.
Table 1. List of biggest cycles of graph Fig.4 regarding condition (*) for each vertex
|
Vertex |
Simple cycle (*) |
Wnd |
Minimized |
|
0010 |
0010-0110-1110-1010-(0010) |
4 |
 |
|
0101 |
0101-0111-(0101) |
2 |
 |
|
0111 |
0111-0101-(0111) |
2 |
 |
|
0111-0110-(0111) |
2 |
 |
|
|
0110 |
0110-1110-1010-0010-(0110) |
4 |
 |
|
1110 |
1110-1010-0010-0110-(1110) |
4 |
 |
|
1011 |
1011-1010-(1011) |
2 |
 |
|
1010 |
1010-0010-0110-1110-(1010) |
4 |
 |
For vertices 0010, 0110, 1110, 1010 cycles are the same. Consequently, the minimized forms are similar, too. For vertex 0111 two appropriate adjacency is available. In other word, the biggest cycle is not unique. If both of them be involved in final minimized function, then one extra statement is imposed to it. So, one of them must be chosen as below:
If vertex V has more than one biggest cycle regarding (*), choose the adjacency that its first vertex (next to proposed V) has less adjacent.
In our example, vertex 0111 has two adjacent 0101 and 0110. First one has 1 adjacent vertex, and second has 3. So, first one has to be chosen and w’xz should appear in final minimized rather than w’xy.
The reason is when you choose the path which its first vertex has less adjacent, probability for this vertex to be included in other adjacencies is less, and if it has no other adjacent vertices, it couldn’t participate in minimization operation. So, to make sure that it never happens, choose the path with less. But, if the number of adjacent vertices for both of them was equal, then you can choose one randomly. Because, they have similar circumstances and it doesn’t differ that which one is selected.
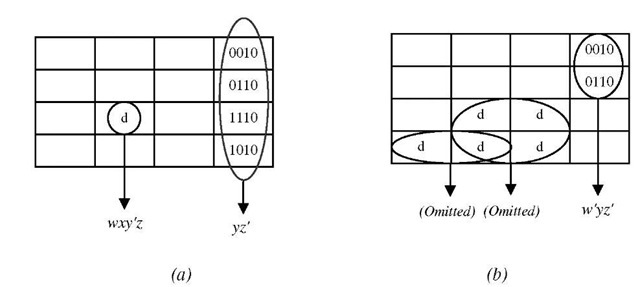
Don’t-care vertices are those which can take 0 or 1, and their value doesn’t matter in final output of function or circuit [19]. When there are don’t-cares in a graph, you have to consider the (**) and (***) strategies to achieve the maximum minimization. (**)
Biggest appropriate cycle should not be found for don’t-care vertices.
We intend to reduce don’t-care vertices, because their existence may impose extra gates to the circuit. Look at the Fig.5 (a). If you propose the adjacency for the single d, then you have added an extra statement to the final minimized function. So, you have to avoid finding biggest appropriate cycle for don’t-care vertices, in order to achieve maximum minimization. This matter causes that adjacencies which consist of pure don’t-care vertices (Wnd=0), be omitted from the final minimized function. For example, look at Fig.5 (b).
Fig. 5. Omitting the cycles with pure don’t-care vertices
If the biggest appropriate cycle for a vertex is not unique, then choose the cycle with greater Wnd.
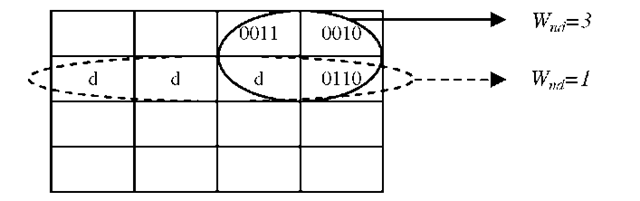
The goal is including more non-don’t-care vertices in minimization. So, the cycle that contains less don’t-cares should be chosen. Fig.6 is an example for this point. It shows the chosen appropriate cycle for vertex 0110.
Fig. 6. Choosing the cycle with greater Wnd
Minimization Algorithm
To implement the maximum minimization on the introduced graph, the algorithm in below is offered.
First, it creates a graph according to Boolean function. Then, it checks whether the function is complete, return 1. Else, find the biggest cycles for each non-don’t-care vertex, and if it wasn’t unique, according the Wnd and first vertex next to V in the cycles chooses the appropriate one. After that, minimizes the adjacency by taking the similar bits and reduce others. Then, it stores the minimized form. When these steps were done for all the vertices, some statements will be created per vertices (as you see in Table.1). After reducing the repeated ones, final minimized function will be achieved and returned.
Conclusion
In this paper, we introduced a heuristic algorithm to apply maximum minimization to SOP Boolean functions that include don’t-care statements. Therefore, graph data structure as the essential base of this algorithm was defined, and two agreements were made which forked from the difference between mathematical definition of simple cycles and what we need for our object. Then, the method of minimization was talked, which used the concepts of Karnaugh map. A solution for the problem of locating a vertex in more than one appropriate adjacency was presented, and also don’t-care statements were included to the solution. Finally, the algorithm of minimization presented.
