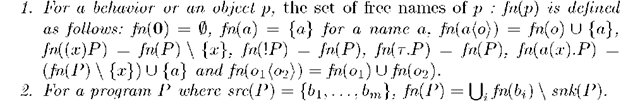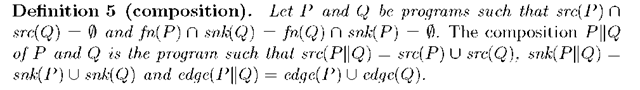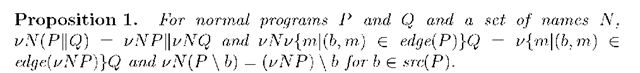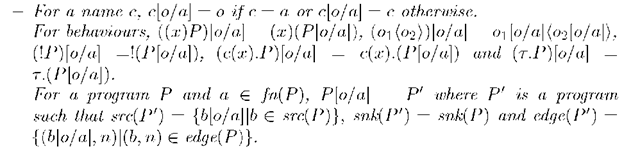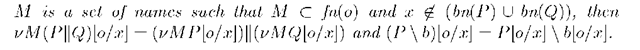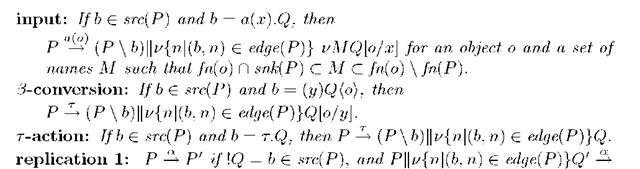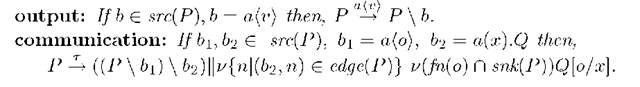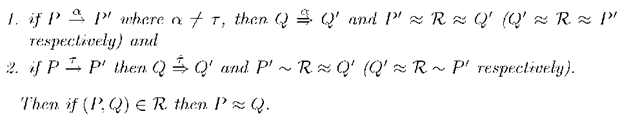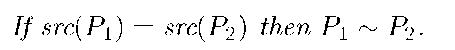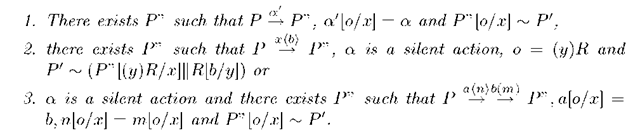Abstract
This paper presents congruence results of a weak equivalence on a graph rewriting model of concurrent processes with higher-order communication. A bipartite directed acyclic graph represents a concurrent system that consists of a number of processes and messages in our model. The model presented here makes it possible to represent local names that their scopes are not nested. We show that weak bisimulation equivalence is a congruence relation w.r.t. operations that correspond to r-prefix, input prefix, new-name, replication, composition and application respectively.
Introduction
LHO(Local Higher Order n-calculus) [12] is a formal model of concurrent systems with higher-order communication. It is a subcalculus of higher order n-calculus[11] with asynchronous communication capability. The calculus has the expressive power to represent many practically and/or theoretically interesting examples that include program code transfer.
On the other hand, as we reported in [5,7,6], it is difficult to represent the scopes of names of communication channels using models based on process algebra. We presented a model that is based on graph rewriting instead of process algebra as a solution for the problem on representation of scopes of names for first-order case [5]. We defined an equivalence relation of processes called "scope equivalence" based on scopes of names.
We showed the congruence results of strong bisimulation equivalence [6] and the scope equivalence [8] for first order case. We extended the the model for systems with higher-order communication[7,9]. And we showed that the congruence results w.r.t. strong bisimulation equivalence for higher-order case[10]. This paper presents the congruence results of weak bisimulation equivalence for the extended model with higher-order communication.
Congruence results on bisimilarity based on graph rewriting models are reported in [1,13]. Those studies adopts graph transformation approach for proof techniques. In this paper, graph rewriting is introduced to extend the model for the representation of scopes of names.
The model presented here is based on graph rewriting system such as [1,2,3,4,13]. We represent a concurrent program consists of a number of processes (and messages on the way) using a bipartite directed acyclic graph. The intuitive description of the model is presented in [9,10].
Formal Definitions
Programs
First, a countably-infinite set of names is presupposed as other formal models based on process algebra.
Definition 1 (program). Programs and behaviours are defined recursively as follows.
(i) Let ai,. ..,ak are distinct names. A program is a a bipartite directed acyclic graph with source nodes bi,.. . ,bm and sink nodes ai,.. . ,a/~ such that
— Each source node bi(1 < i < m) is a behaviour. Duplicated occurrences of the same behavior are possible.
— Each sink node is a name aj (1 < j < k). All aj’s are distinct.
— Each edge is directed from a source node to a sink node. Namely, an edge is an ordered pair (bi,aj) of a source node and a name. For any source node bi and a name aj there is at most one edge from bi to ai.
For a program P, we denote the multiset of all source nodes of P as src(P), the set of all sink nodes as snk(P) and the set of all edges as edge(P). Note that the empty graph: 0 such that src(0) = snk(0) = edge(0) = 0 is a program.
(ii) A behavior is an application, a message or a node consists of the epidermis and the content defined as follows. In the following of this definition, we assume that any element of snk(P) nor x does not occur in anywhere else in the program.
1. A node labeled with a tuple of a name: n (called the subject of the message) and an object: o is a message and denoted as n(o).
2. A tuple of a variable x and a program P is an abstraction and denoted as (x)P. An object is a name or an abstraction.
3. A node labeled with a tuple of an abstraction and an object is an application. We denote an application as A{o) where A is an abstraction and o is an object.
4. A node whose epidermis is labeled with "!" and the content is a program P is a replication, and denoted as !P.
5. An input prefix is a node (denoted as a(x).P) that the epidermis is labeled with a tuple of a name a and a variable x and the content is a program P.
6. A t-prefix is a node (denoted as t.P) that the epidermis is labeled with a silent action t and the content is a program P.
Definition 2 (locality condition). A program P is local if for any input prefix c(x).Q and abstraction (x)Q occurring in P, x does not occur in the epidermis of any input prefix in Q. An abstraction (x)P is local if P is local. A local object is a local abstraction or a name.
Definition 3 (free/bound name)
The set of bound names of P (denoted as bn(P)) is the set of all names that occur in P but not in fn(P) (including elements of snk(P) even if they do not occur in any element of src(P)).
Definition 4 (normal program).
A program P is normal if for any b G src(P) and for any n G fn(b) O snk(P), (b, n) G edge(P) and any programs occur in b is also normal.
It is quite natural to assume the normality for programs. So in this paper, we consider normal programs only.
Intuitively, P||Q is the parallel composition of P and Q. Note that we do not assume snk(P) O snk(Q) = 0. Obviously PHQ = QHP and ((P||Q)||R) = (P||(Q||R)) for any P,Q and R from the definition. The empty graph 0 is the unit of "||". Note that src(P) Usrc(Q) and edge(P) Uedge(Q) denote the multiset unions while snk(P) U snk(Q) denotes the set union.
It is easy to show that for normal and local programs P and Q, P| Q is normal and local.
Definition 6 (n-clusure). For a normal program P and a set of names N such that NObn(P) = 0, the N-closure vN(P) is the program such that src(vN(P)) =
for a program P
We sometimes denote
Definition 7 (deleteing a behaviour).
For a normal program
src(P), P \ b is a program such that
mean the multiset
Definition 7 (deleteing a behaviour).
src(P), P \ b is a program such that
Note that
subtractions. We can show the following propositions from the definitions.
Definition 8 (context). Let P be a program and b G src(P) where b is an input prefix, a t-prefix or a replication and the content of b is 0. A simple first-order context is the graph P[ ] such that the content 0 of b is replaced with a hole "[ ]". We call a simple context as a T-context, an input context or a replication context if the hole is the content of a t-prefix, of an input prefix or of a replication respectively.
Let P be a program such that b G src(P) and b is an application (x)0(Q). A simple application context P[ ] is the graph obtained by replacing the behaviour b with (x)[ ](Q). A simple context is a simple first-order context or a simple application context.
A context is a simple context or the graph P[Q[ ]] that is obtained by replacing the hole of P[ ] replacing with Q[ ] for a simple context P[ ] and a context Q[ ] (with some renaming of the names occur in Q if necessary).
For a context P [ ] and a program Q, P [Q] is the program obtained by replacing the hole in P[ ] by Q (with some renaming of the names occur in Q if necessary).
Operational Semantics
Definition 9 (substitution). Letp be a behavior, an object or a program and o be an object. For a name a, we assume that a G fn(p). The mapping [o/a] is a substitution if p[o/a] is defined as follows respectively.
For the cases of abstraction and input prefix, note that we can assume
because
rename x if necessary).
Definition 10 (acceptable substitution). Letp be a local program or a local object. A substitution [a/x] is acceptable for p if for any input prefix c(y).Q occurring in
In any execution of local programs, if a substitution is applied by one of the rules of operational semantics then it is acceptable. Thus in the rest of this paper, we consider acceptable substitution only for a program, a context or an abstraction. Namely we assume that [o/a] is applied only for the objects such that a does not occur as a subject of input prefix. This is the reason
In any execution of local programs, if a substitution is applied by one of the rules of operational semantics then it is acceptable. Thus in the rest of this paper, we consider acceptable substitution only for a program, a context or an abstraction. Namely we assume that [o/a] is applied only for the objects such that a does not occur as a subject of input prefix. This is the reason
Proposition 2. Let P and Q are normal programs and o be an object. If
Definition 11 (action). For a name a and an object o, an input action is a tuple a(o) and an output action is a tuple a(o). An action is a silent action t, an output action or an input action.
Definition 12 (labeled transition). For an action a, ^ is the least binary relation on normal programs that satisfies the following rules.
P’, where Q is a program obtained from Q by renaming all names in snk(R) to distinct fresh names that do not occur in anywhere else, for all R’s where each R is a program that occur in Q (including Q itself).
P’, where Q is a program obtained from Q by renaming all names in snk(R) to distinct fresh names that do not occur in anywhere else, for all R’s where each R is a program that occur in Q (including Q itself).
Q by renaming all names in snk(R) to distinct fresh names that do not occur in anywhere else, for all R’s where each R is a program that occur in Q (including Q itself).
Q by renaming all names in snk(R) to distinct fresh names that do not occur in anywhere else, for all R’s where each R is a program that occur in Q (including Q itself).
We can show that for any program P, P’ and any action a such that
if P is local then P’ is local and if P is normal then P’ is normal. The following propositions are straightforward from the definitions.
Proposition 3. For any normal programs P,P’ and Q, and any action a if
Proposition 4. For any program P, Q and R and any action
is derived by one of input, ^-conversion, T-action or output immediately,
Proposition 4. For any program P, Q and R and any action is derived by one of input, ^-conversion, T-action or output immediately,
Definition 13 (substitution for actions). For a substitution
Note that
as we consider local programs.
Definition 14 (strong bisimulation equivalence). A binary relation R on normal programs is a strong bisimulation if for any P and Q such that
that for any a and
then there exists Q’ such that for any a and
equivalence ~ is defined as follows:
for some strong bisimulation R.
Definition 15 (strong bisimulation up to A binary relation R on normal programs is a strong bisimulation up to ~ if for any P and Q such that
such that for any
then there exists Q’ such that for any
Proposition 5. If R is a strong bisimulation up to then ~ R ~ is a strong bisimulation.
We denote
if and only if
and
Definition 16 (weak bisimulation equivalence). A binary relation TZ on normal programs is a weak bisimulation if: for any P and Q such that
for any a and
then there exists Q’ such that
Weak bisimulation equivalence
for some weak bisimulation R.
We have the following proposition from the definitions. The outline of the proof of the following proposition is similar to that of Exercise 2.4.64 in [12].
Proposition 6. Suppose R is such that for any P, Q such that
Congruence Results
Proposition 7.
Proof (outline). We can show that
is a strong bisimulation from the definitions.
Proposition 8. Let P be a normal program, a be an action, [o/x] be a substitution that is acceptable to
that does not occur elsewhere and M be a set of names such that
If
then one of the followings holds.
Conclusions and Discussions
This paper presented congruence results of weak bisimulation equivalence w.r.t. composition, T-context, input context, replication context and application context for the graph rewriting model of concurrent systems.