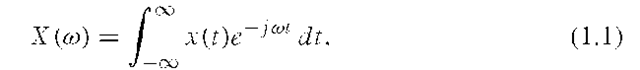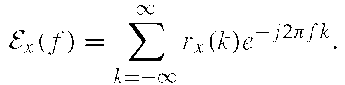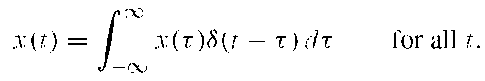The concepts of a signal and a system are crucial to the topic. We will consider time as well as frequency domain models of the signals. We focus on signals and system components that are important to study software-defined GPS and Galileo receiver design.
Characterization of Signals
In satellite positioning systems, we encounter two classes of signals referred to as deterministic and random signals. Deterministic signals are modeled by explicit mathematical expressions. The signals
are examples of deterministic signals. A random signal, on the other hand, is a signal about which there is some degree of uncertainty. An example of a random signal is a received GPS signal: the received signal contains beside the information bearing signal also noise from disturbances in the atmosphere and noise from the internal circuitry of the GPS receiver.
Now some basic topics on deterministic and stochastic signal theory are reviewed and simultaneously we establish a notation.
A reader familiar with random processes knows concepts like autocorrelation function, power spectral density function (or power spectrum), and bandwidth. These concepts can be applied for deterministic signals as well, and that is exactly what we intend to do in the following.
Continuous-Time Deterministic Signals
Let us consider a deterministic continuous-time signal x(t), real- or complex-valued with finite energy defined as
The symbol denotes the absolute value, or magnitude, of the complex quantity. In the frequency domain this signal is represented by its Fourier transform:
where
and the variable
denotes angular frequency. By definition
and the units for
and f are radian and cycle, respectively. In general, the Fourier transform is complex:
The quantity
is often referred to as the spectrum of the signal x (t) because the Fourier transform measures the frequency content, or spectrum, of x(t). Similarly, we refer to
as the magnitude spectrum of x (t), and to arg
= arctan
as the phase spectrum of x (t). Moreover, we refer to 
as the energy density spectrum of x (t) because it represents the distribution of signal energy as a function of frequency. It is denoted
The inverse Fourier transform x(t) of
is
We say that x (t) and
constitute a Fourier transform pair:
The energy density spectrum
of a deterministic continuous-time signal x (t) can also be found by means of the (time-average) autocorrelation function (ACF) of the finite energy signal x (t). Let * denote complex conjugation, and then the ACF of x (t) is defined as
is defined as and the energy density spectrum
is defined as
Again, we say that
constitute a Fourier transform pair:
Discrete-Time Deterministic Signals
Let us suppose that x(n) is a real- or complex-valued deterministic sequence, where n takes integer values, and which is obtained by uniformly sampling the continuous-time signal x(t); read Section 1.2. If x(n) has finite energy
then it has the frequency domain representation (discrete-time Fourier transform)
or equivalently
It should be noted that X (f) is periodic with a period of one and
is periodic with a period of
The inverse discrete-time Fourier transform that yields the deterministic sequence x(n) from
or X (f) is given by
Notice that the integration limits are related to the periodicity of the spectra. We refer to
as the energy density spectrum of x(n) and denote it as
The energy density spectrum
of a deterministic discrete-time signal x(n) can also be found by means of the autocorrelation sequence
via the discrete-time Fourier transform
That is, for a discrete-time signal, the Fourier transform pair is
Unit Impulse
In signal analysis a frequently used deterministic signal is the unit impulse. In continuous time the unit impulse
, also called the delta function, may be defined by the following relation:
where x (t) is an arbitrary signal continuous at t = 0. Its area is
FIGURE 1.1. Rectangular pulse.
In discrete time the unit sample, also called a unit impulse sequence, is defined as
It follows that a continuous-time signal x (t) may be represented as
Similarly, a sequence x(n) may be represented as
The Fourier transform of the unit impulse
is given by
which gives us the following Fourier transform pair:
The spectrum of the unit sample is obtained by
which gives us the following Fourier transform pair:
