Galileo Signal (GPS and Galileo Receiver) Part 3

Message Structure

This section outlines the Galileo message structure.

Frames and Pages

The message is composed of frames, see Figure 3.8. The frame is composed of several subframes, and each subframe again is composed of several pages. The page is the basic structure for the navigation message and contains the following fields:

- a synchronization word (SW),

- a data field,

- a cyclic redundancy check (CRC) bits for error detection, and

- tail bits for the forward error correction (FEC) encoder containing all zeros. CRC and data encoding are used to provide better signal and data integrity. For L1 OS the synchronization word is a fixed 10-bit sequence. All data are encoded using the following bit and byte ordering:

- for numbering, the most significant bit/byte is numbered as bit/byte 0,

- for bit/byte ordering, the most significant bit/byte is transmitted first.

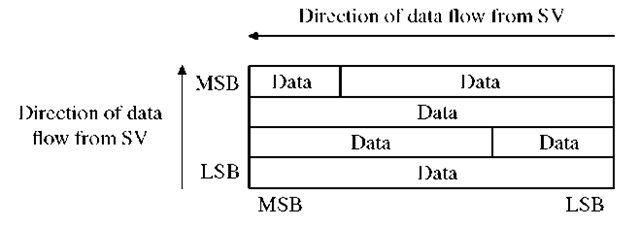
In Figure 3.9 the most significant bit is placed left, the less significant bit is placed to the right, the most significant items at the top, and the less significant items at the bottom.

Cyclic Redundancy Check

The CRC algorithm accepts a binary data frame, corresponding to a polynomial M , and appends a checksum of r bits, corresponding to a polynomial C.

FIGURE 3.9. Ordering principle for data.

The concatenation of the input frame and the checksum then corresponds to the polynomialsince multiplying bycorresponds to shifting the input frame r bits to the left. The algorithm chooses the checksum C such that T is divisible by a predefined polynomial P of degree r, called the generator polynomial.

The algorithm dividesby P and sets the checksum equal to the binary vector corresponding to the remainder. That is, if. where R is a polynomial of degree less than r, then C = R and the checksum is the binary vector corresponding to R. If necessary, the algorithm preceds zeros to the checksum so that it has length r. The MATLAB CRC generator does the following:

1. Left-shift the input frame by r bits and divide the corresponding polynomial by P.

2. Set the checksum equal to the binary vector of length r corresponding to the remainder from step 1.

3. Append the checksum to the input data frame. The result is the output frame.

The CRC algorithm uses binary vectors to represent binary polynomials, in descending order of powers. For example, the vectorrepresents the polynomial

Example 3.1 Suppose the input frame iscorresponding to the polynomialand the generator polynomial is

of degree r = 3. By polynomial division Remember that any binary number added to itself in a modulo-2 field yields zero. The remainder is R = x so that the checksum is then Note that an extra 0 is added on the left to make the checksum have length 3.

Forward Error Correction and Block Interleaving

The starting point is a digital information source (transmitter) that sends a data sequence comprising k bits of data to an encoder. Employing forward error-correction coding, the encoder inserts redundant bits, thereby outputting a longer sequence of n code bits called a codeword. At the receiving end, codewords are used by a suitable decoder to extract the original data sequence.

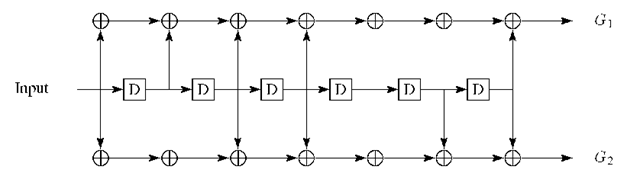
FIGURE 3.10. Viterbi convolutional coding scheme.

In general, codes are designated with the notation (n, k) according to the number of n output code bits and k input data bits. The ratio k/n is called the rate of the code and is a measure of the fraction of information contained in each code bit.

Figure 3.10 describes the Viterbi convolutional coding scheme used for Galileo. The Viterbi convolutional coding of all data channels is characterized by the following values: coding rate = 1 /2, constraint length 7, generator polynomials

and encoding sequenceand then That is, there are taps at seven points along the encoder shift register, and it generates two encoded channel symbols for each input data bit. Note that (octal) is 001111001 in binary and(octal) is 001011011 in binary.

We observe that forthe taps 1, 4, 5, 6, and 7, numbered from right to left, are connected to modulo-2 adders and for G2 the taps 1, 2, 4, 5, and 7 are connected to modulo-2 adders. The error-correcting power is related to the constraint length, increasing with longer lengths of shift register.

After the Viterbi convolutional encoding block follows an interleaving procedure. The purpose of interleaving is to increase the efficiency of the convolutional coding by spreading the burst errors in order to improve the correction capacity of the specific convolutional decoding algorithm applied in the receiver.

Normally interleaving is implemented by using a two-dimensional buffer array. The data enter the buffer array row by row and are then read out column by column. The result of the interleaving process is ideal if a burst of errors in the communication channel after de-interleaving becomes spaced single-symbol errors, which are easier to correct than consecutive ones.

Example 3.2 Below we illustrate how an input data stream is read, column by column, into an array and then read out, row by row, to achieve the bit interleaving operation:

- Data input

- Interleaving array

TABLE 3.2. Galileo ephemeris parameters

Parameter	No. of Bits	Scale Factor	Unit
	32		semicircle
	16		semicircle/s
	32		dimensionless
	32		mi/2
	32		semicircle
	32		semicircle
	32		semicircle
	24		semicircle/s
	14		semicircle/s
	16		radian
	16		radian
	16		m
	16		m
	16		radian
	16		radian
	14		s
	9		—

- Interleaved data output for transmission

This block interleaving has interleaving depth 4. In this simple example three consecutive errors in the transmitted data, let us sayare translated into three isolated, single errors in the de-interleaved data.

Message Contents

The freely accessible navigation message on L1 OS contains all parameters necessary to compute the position of a Galileo satellite, clock correction parameters, parameters for conversion of Galileo System Time (GST) to UTC and GPS Time (GPST), and service parameters including an almanac.

A Galileo ephemeris contains 17 parameters as defined in Table 3.2. The unit semicircle is converted to radian by multiplication with

A Galileo ephemeris is valid for four hours. Every three hours a new ephemeris is uploaded. Hence an overlap of one hour occurs. And four ephemerides cover a 12-hour orbit prediction.

The geocentric coordinatesof satellite k (the superscript k denotes satellite k, and not the power k) at timeare given as

For a definition of the parameterssee Figure 8.5. The quantities

are evaluated for t according to the following procedure:

As usual the mean Earth rotation rate is denotedThis algorithm is similar to the one for GPS and is coded as the M-file satpos. The function computes the position of any Galileo satellite at any time. It is fundamental to every position calculation.