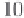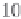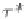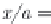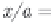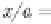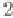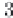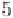Geoscience Reference
In-Depth Information
T
g(g
H
)
1
/
2
2
d
t
,
W
=
ρ
ξ
(2.84)
0
where
T
is the duration of the wave perturbation. From formulae (2.80) and (2.81) it
is seen that the wave energy is conveniently normalized to the quantity
W
0
=
ag
2
0
,
representing the potential energy of a free-surface rectangular elevation of length
2
a
and height
ρη
η
0
. Precisely such an elevation should arise on the water surface
in the case of a impulse piston-like displacement of the seabed (if the process is
described within the framework of the linear theory of long waves).
Owing to the problem considered being linear, the tsunami wave amplitude is
proportional to the seabed (ocean bottom) deformation amplitude. In the case of
short motions the amplitude is independent of the duration of the displacement or
the horizontal size of the source and amounts to half the amplitude of the seabed de-
formation. When the displacements are longer in time (
τ
∗
1), the amplitude drops
τ
∗
)
−
1
. The dependencies (2.78) and (2.79) are
shown in Figs. 2.12 and 2.13, respectively, by broken lines.
From formulae (2.80) and (2.81) it follows that the energy of a tsunami wave is
proportional to the square amplitude of the seabed deformation
monotonously according to the law (
η
0
and to the hori-
zontal dimension of the source
a
. The respective dependences are shown in Fig. 2.14
(curve 3). In the case of a piston-like displacement the wave energy decreases
monotonously as the duration of the seabed deformation increases. In the case of
.
.
.
.
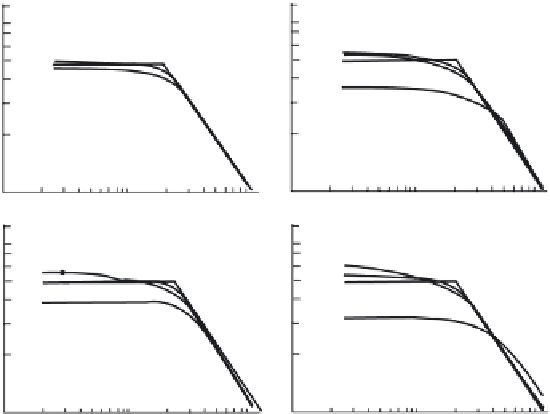
Fig. 2.12 Maximum amplitude of wave, excited by piston-like displacement of seabed, versus
displacement duration for various distances from the generation area. Curves 1-3 correspond to
values of parameter
a
/
H
= 1
,
3
,
9. The broken line represents linear theory of long waves