Geoscience Reference
In-Depth Information
Für einen Vektor ist der Laplace-Operator (in kartesi-
schen Koordinaten) definiert durch:
Tab. 7.11
erf
.—/
und erfc
.—/
—
erf
.—/
erfc
.—/
—
erf
.—/
erfc
.—/
0,00
0,000 000
1,000 000
1,1
0,880 205
0,119 795
grad div
v
rot rot
v
Dr.r
v
/ r.r
v
/
0,05
0,056 372
0,943 628
1,2
0,910 314
0,089 686
0
1
0,10
0,112 463
0,887 537
1,3
0,934 008
0,065 992
@
2
v
1
@
x
1
@
2
v
1
@
x
2
@
2
v
1
@
x
3
C
C
0,15
0,167 996
0,832 004
1,4
0,952 285
0,047 715
@
A
:
@
2
v
k
@
x
i
:
D
@
2
v
2
@
@
2
v
2
@
@
2
v
2
@
D
v
Dr
2
v
D
C
C
0,20
0,222 703
0,777 297
1,5
0,966 105
0,033 895
x
1
x
2
x
3
0,25
0,276 326
0,723 674
1,6
0,976 348
0,023 652
@
2
v
3
@
x
1
@
2
v
3
@
x
2
@
2
v
3
@
x
3
C
C
0,30
0,328 627
0,671 373
1,7
0,983 790
0,016 210
0,35
0,379 382
0,620 618
1,8
0,989 091
0,010 909
0,40
0,428 392
0,571 608
1,9
0,992 790
0,007 210
0,45
0,475 482
0,524 518
2,0
0,995 322
0,004 678
7.5 Die Fehlerfunktion
0,50
0,520 500
0,479 500
2,1
0,997 021
0,002 927
0,55
0,563 323
0,436 677
2,2
0,998 137
0,001 863
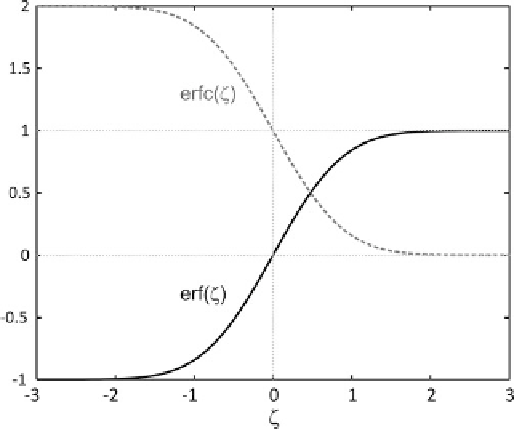
Als (gaußsche) Fehlerfunktion (
error function
)wirddasIn-
tegral
0,60
0,603 856
0,396 144
2,3
0,998 857
0,001 143
0,65
0,642 029
0,357 971
2,4
0,999 311
0,000 689
0,70
0,677 801
0,322 199
2,5
0,999 593
0,000 407
Z
—
0,75
0,711 156
0,288 844
2,6
0,999 764
0,000 236
p
e
x
2
dx
erf
.—/ D
(7.1)
0,80
0,742 101
0,257 899
2,7
0,999 866
0,000 134
0,85
0,770 668
0,229 332
2,8
0,999 925
0,000 075
0
0,90
0,796 908
0,203 092
2,9
0,999 959
0,000 041
0,95
0,820 891
0,179 109
3,0
0,999 978
0,000 022
bezeichnet, dessen Argument
—
komplex oder reell sein kann.
Entsprechend ist die komplementäre Fehlerfunktion durch
erfc
.—/ D 1
erf
.—/
definiert. Der Name der Fehlerfunktion
deutet auf ihre Bedeutung in der Statistik hin, wo sie eng mit
dem Fehlerintegral zusammenhängt, der Verteilungsfunkti-
on der gaußschen Normalverteilung. Darüber hinaus findet
sie viele Anwendungen bei der Lösung partieller Differenzi-
algleichungen. Für Argumente zwischen null und unendlich
nehmen die beiden Fehlerfunktionen Werte zwischen null
Problemen wird vor allem von der Ableitung der Fehlerfunk-
tion und den Integralen der komplementären Fehlerfunktion
Gebrauch gemacht:
1,00
0,842 701
0,157 299
3,1
0,999 988
0,000 012
d
2
d
—
2
d
d
—
p
p
e
—
2
I
—
e
—
2
I
erf
.—/ D
erf
.—/ D
Z
p
D
e
—
2
ierfc
.—/
erfc
.
x
/
dx
D
—
erfc
.—/I
—
Z
(7.2)
D
i
2
erfc
.—/
ierfc
.
x
/
dx
7.6 Legendre-Transformation
—
p
—
e
—
2
1
4
.1 C 2—
2
/
erfc
.—/
D
Diese nach dem französischen Mathematiker Adrien-
Marie Legendre (1752-1833) benannte sogenannte Be-
rührungstransformation ist ein Verfahren zur Variablen-
Transformation. Sie beschreibt eine Funktion einer oder
mehrerer Variablen durch ihre partiellen Ableitungen, den
unabhängigen Variablen einer neuen Funktion. Dies soll
zunächst am Beispiel einer Funktion einer Veränderlichen
1
4
Œ
erfc
.—/ 2—
ierfc
.—/ :
D
Weitere Eigenschaften und Reihenentwicklungen finden sich
in mathematischen Tabellenwerken (z. B. Abramowitz und