Wärme und Temperaturfeld der Erde - Einfuhrung in die Geophysik - page 320

Auflösen von ( 6.202 ) nach v z und Einsetzen in ( 6.204 ) liefert
eine Gleichung für T 0 :

@ 4 T 0
@ x 4

@ 4 T 0
@ x 2 @ z 2

@ 4 T 0
@ z 4

k ' f .¡ f / 2 c f g . T o T u /

œ`

@ 2 T 0
@ x 2 :
(6.205)

C 2 C D

Aus den Randbedingungen für die Temperaturstörung
T 0 D 0 für z D 0 , ` erhält man direkt jene für die zweiten
Ableitungen nach x:

@ 2 T 0 =@ x 2

D 0 für z D 0 , ` .Ge-

meinsam mit v z

D 0 D 0 `

erhält man aus ( 6.202 )
die Randbedingungen für die zweiten Ableitungen nach
z: @ 2 T 0 =@ z 2 D 0 für z D 0 , ` . Eine Elementarlösung für
( 6.205 ) , welche diese Randbedingungen erfüllt, ist:

bei z ,

Abb. 6.44 Freie Konvektion in porösem Gestein (nach © Turcotte &
Schubert 2002 )

klein gegen die linearen und können vernachlässigt werden:

T 0 D T 0 0 sin z
`

sin 2 x
ƒ

;

@ 2 T 0
@

/ f v z T o T u

@ 2 T 0
@

T 0
@

/ @ œ C D .¡ c

t C .¡

c :

x 2 z 2

`

wo T 0 0 die Amplitude der Temperaturstörung ist und ƒ ihre
Wellenlänge. T 0 0 kann mit Hilfe der linearen Störungstheorie
nicht bestimmt werden, wohl aber

(6.199)

ƒ . Einsetzen in ( 6.205 )

Außerdem gilt:

ergibt:
" 2 `
ƒ

# 2 2 `
ƒ

k ' f ¡ f 2 c f g `. T u T o /
œ

@ v 0 x @ v z

2 2

r v 0 D

@ x C @ z D 0

(6.200)

C 2

D :

„ ƒ‚ …

sowie die Darcy-Gleichung ( 7.41 ) zur Beschreibung der
durch die Druckstörung p 0 angetriebenen Strömung im po-
rösen Gestein:

Ra

(6.206)

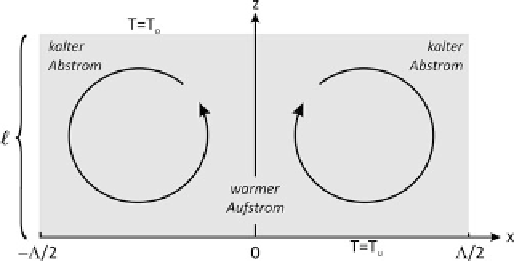
Hierbei repräsentiert die Rayleigh-Zahl Ra die Parameter-
kombination, für die in einer von unten beheizten porösen
Gesteinsschicht freie Konvektion der Wellenlänge

@ p 0
@ z ' f ¡ f gT 0

@ p 0
@

k k

v 0 x D v z D

x I

; (6.201)

ƒ ent-

steht:

wobei ' f der thermische Ausdehnungskoeffizient des Fluids
ist, und seine Dichtevariation ¡ f D '¡ f T 0 hier wie im
Abschn. 7.11.3 im Anhang bezüglich der Störung T 0 des
konduktiven Temperaturprofils T k definiert ist. Zu Beginn
der freien Konvektion herrschen nahezu stationäre, konduk-
tive Verhältnisse. Daher entfällt die Zeitableitung in ( 6.199 ) ,
und man erhält:

k ' f ¡ f 2 c f g `. T u T o /
œ

Ra D

:

(6.207)

Als kritisch wird wiederum jene Rayleigh-Zahl Ra krit be-
zeichnet, bei welcher freie Konvektion gerade einsetzt. Ab-
leiten von ( 6.206 ) nach 2 `=ƒ und zu null setzen ergibt die
zur minimalen kritischen Rayleigh-Zahl gehörigeWellenlän-
ge:

@ 2 T 0
@ x 2

/ f v z T o T u
`

@ 2 T 0
@ z 2

œ C D .¡ c : (6.202)

ƒ=.2`/ D 1 bzw. ƒ D 2` : (6.208)

Die Druckstörung p 0 kann aus ( 6.201 ) durch Überkreuz-
Ableiten und Subtrahieren eliminiert werden:

Setzt man dies wieder in ( 6.206 ) ein, erhält man Ra krit D
.2 2 / 2 = 2 D 4 2 . Damit beträgt die minimale kritische
Rayleigh-Zahl für freie Konvektion in einer von unten be-
heizten porösen Gesteinsschicht:

@ v 0 x
@ z

@ v z
@ x D

k ' f ¡ f g @ T 0

@ x :

(6.203)

Ebenso wird v 0 x aus ( 6.200 ) und ( 6.203 ) eliminiert und man
erhält schließlich mit @ 2 v 0 x =.@ x @ z / D@ 2 v z =@ z 2 :

Ra min
krit

D 4 2 D 39;4784 40 : (6.209)

Aus ( 6.207 ) kann man den minimalen kritischen Tempera-
turgradienten

@ 2 v z
@ x 2

@ 2 v z
@ z 2

k ' f ¡ f g @ 2 T 0

@ x 2 :

/ krit bestimmen, ab dem freie Konvekti-
on einsetzt, indem man Ra

. dT = dz

C D (6.204)

D 4 2 setzt und ( 6.206 ) nach