Wärme und Temperaturfeld der Erde - Einfuhrung in die Geophysik - page 317

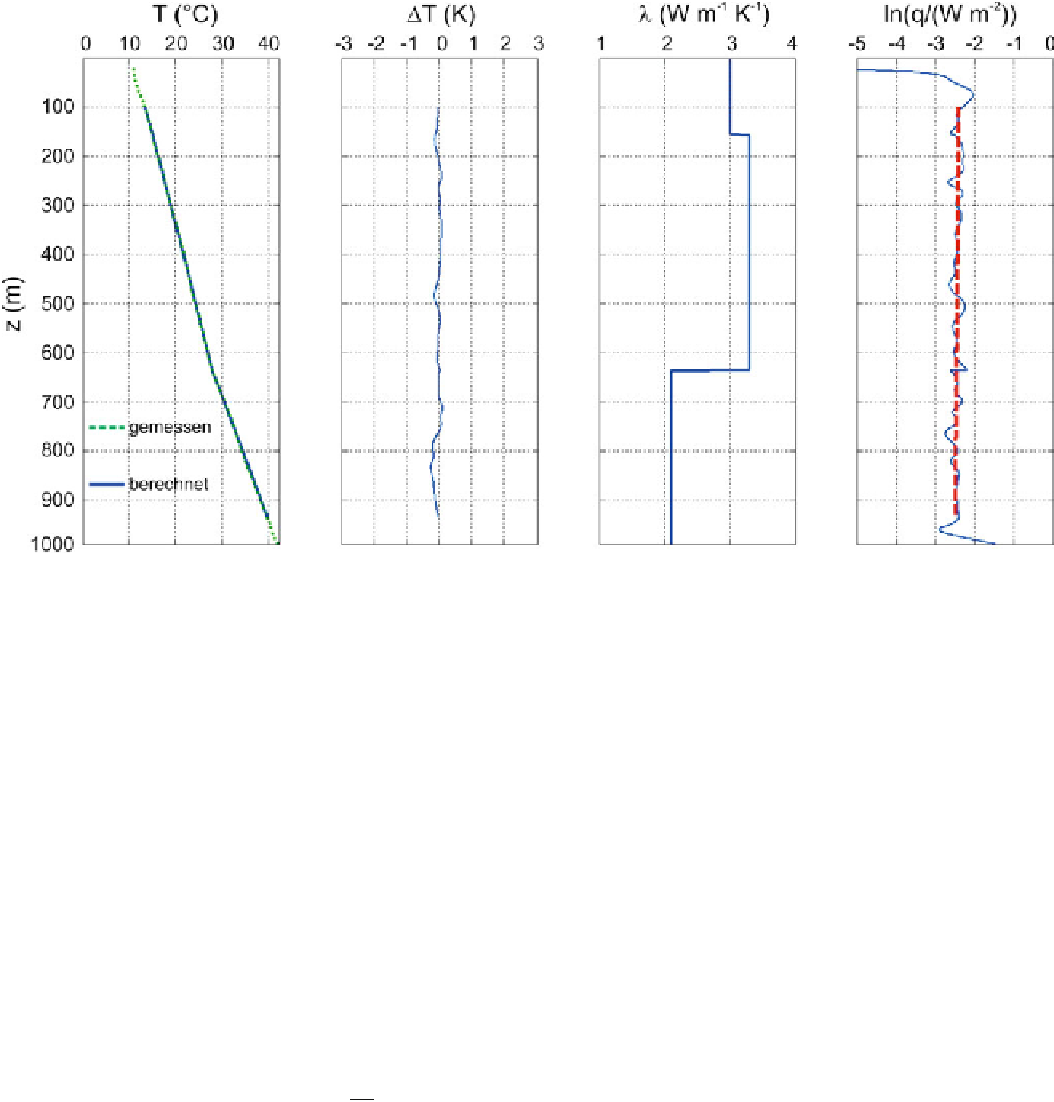
Abb. 6.41 1-D Péclet-Zahl-Analyse des Temperaturprofils der Boh-
rung Frankenthal-4: Die Steigung von Pe

entspricht einer im Intervall von 100 m bis 935 m (L D 835 m) ab-

D 1;057 10 4 m 1
der Regression von ln q gegen die Tiefe ( gestrichelte rote Gerade )

strömenden Volumenstromdichte von 2,27 mm a 1

= L

— D . z z 0 / ,alsod — D dz folgt schließlich: isotrope Wärmeleitfähigkeit sowie entweder vernachläs-

sigbare Wärmeproduktionsrate oder eine vorab um deren
Beitrag reduzierte Temperatur vorausgesetzt. Damit lautet
( 6.187 ) :

dq
d —

Pe
L q D 0

(6.192)

@ 2 T
@ x 2

D .¡ c / f v x @ T

@ 2 T
@ z 2 @ x C v z @ T

(man beachte, dass — hier abweichend von ( 6.188 ) definiert
ist). Die charakteristische Gleichung für ( 6.192 ) ist dann
r Pe = L D 0 ,worausr D Pe = L folgt. Als Lösung von
( 6.192 ) erhält man somit q .—/ D Ce — Pe = L . Mit der Rand-
bedingung q .0/ D q 0 erhält man als Lösung von ( 6.192 ) :
q .—/ D q 0 e — Pe = L bzw. q . z z 0 / D q 0 e . zz0 / Pe = L . Logarith-
mieren ergibt mit

œ C : (6.194)

@ z

Das Ziel der Dimensionsanalyse ist die Reduktion der Zahl
der Variablen durch Zusammenfassung zu dimensionslosen
Kennzahlen. Ein Beispiel hierfür ist der gerade behandelte
Fall der 1-D Péclet-Zahl-Analyse, wo die Anzahl der Va-
riablen in ( 6.187 ) von insgesamt sechs (T, z, ¡ f ,c f , œ ,v)
auf nur noch drei ( ‚ , — ,Pe)in( 6.189 ) reduziert wurde.
Für die 2-D Péclet-Zahl-Analyse werden mit den horizon-
talen und vertikalen Fließraten pro Einheitsquerschnitt Q H
bzw. Q V und den in Abb. 6.42 bezeichneten Größen die
folgenden (groß geschriebenen) charakteristischen (dimen-
sionslosen) Variablen definiert: Die Längen X D x

Pe
L bzw.
ln q . z z 0 / D ln q 0 C . z z 0 /

.—/ D ln q 0 C —

ln q

Pe
L

(6.193)

L und
Z D z = D; die Temperatur ‚ D . T T o /=. T u T o / ;die
auf die 2-D Querschnittslängen D und L des Strömungs-
systems (Abb. 6.42 ) normierten spezifischen Flussdichten:
v H D Q H =

=

eine lineare Gleichung in — D z z 0 mit dem Achsenab-
schnitt ln q 0 und der Steigung Pe = L. Somit kann man den
Quotienten Pe = L(sieheAbb. 6.39 ) , wie in Abb. 6.41 gezeigt,
aus der Steigung der linearen Regression von ln q gegen —
bzw.

.

z z 0 / D, v V D Q V = gewinnen. L; die normierten (dimensionslosen)

Darcy-Geschwindigkeiten v i D v x = v H ;v k D v z = v V ,wov x
und v z die Darcy-Geschwindigkeiten in X- und Z-Richtung
sind. Für die Dimensionen gilt demnach:

6.5.5.2 Dimensionsanalyse thermischer Systeme
Ausgangspunkt der Betrachtungen ist die Diffusions-
Advektionsgleichung in zwei Dimensionen. Wie im Ab-
schn. 6.5.5.1 werden stationäre Verhältnisse, homogene und

ΠQ H D ΠQ V D

m 2 s 1 ; . Unter Beach-

tung der Kettenregel erhält man mit diesen Definitionen aus

Πv H D Πv V D ms 1 ; Πv i D Πv k D 1