Geoscience Reference
In-Depth Information
Tab. 6.20
Mittelwerte von Dichte
¡
, isobarer spezifischer Wärmekapazität c
p
, Wärmeleitfähigkeit
œ
, Schwerebeschleunigung g und thermischem
Ausdehnungskoeffizienten
'
c
p
(J kg
1
K
1
)
œ
(Wm
1
K
1
)
g(ms
2
)
'
(
10
6
K
1
)
Mantel
4748
1205
7,9
10,12
17,9
oberer Mantel
3722
1231
5,1
10,17
27,6
bene freie Konvektionsströmung setzt auch im Mantel ein,
wenn die minimale kritische Rayleigh-Zahl überschritten
wird. Deren Wert variiert je nach den getroffenen Annahmen
sowie thermischen und strömungsmechanischen Randbedin-
der Wärmeproduktionsrate A intern beheizte Fluidschicht
mit gekühltem oberem und adiabatischem unteren Rand ist
¡
0
g
'
A
`
5
›œ
¡
0
g
'
A
0
`
5
›œ
¡
0
c
p
g
'
A
0
`
5
œ
2
Ra
D
D
D
;
(6.108)
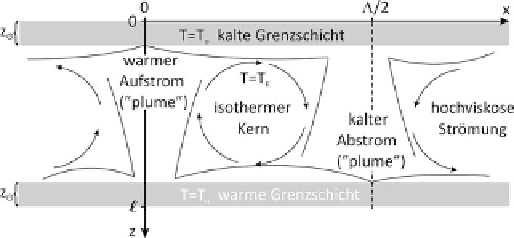
Abb. 6.16
Warme und kalte Grenzschichten bei zweidimensionaler
stationärer, freier Konvektion eines an der Rändern freien Fluids in
einer von oben gekühlten und von unten beheizten Schicht der Mäch-
tigkeit
wobei A
0
D
A
=¡
die auf die Masse bezogene spezifische
Wärmeproduktionsrate ist mit einem Wertebereich im Erd-
mantel von
2;8 10
12
Wkg
1
A
0
5;1 10
12
Wkg
1
gibt sich aus der Analyse postglazialer Hebungen zu
te der anderen Größen sind aus den in Tab.
7.8
aufgeführten
Daten für den gesamten bzw. den oberen Mantel berechnet.
zifischer Wärmeproduktionsrate Rayleigh-Zahlen für den
gesamten Mantel von
2;010
8
Ra
3;710
8
und für den
oberen Mantel von
2;2 10
5
Ra
3;9 10
5
. Diese über-
steigen die kritischen Werte der Rayleigh-Zahl in Tab.
7.13
ummehrere Größenordnungen. Bereits vor 80 Jahren schloss
hieraus der britische Geologe und Geochronologe Arthur
zum Antrieb der Kontinentaldrift erforderlichen Mechanis-
erste, aus physikalischen Überlegungen abgeleitete Antwort
auf die seit der Postulierung von Alfred Wegeners Hypothe-
se der Kontinentaldrift offene Frage nach der Antriebskraft
für die Verschiebung der Kontinente.
Mit Hilfe der linearen Störungstheorie kann ermittelt wer-
den, ob sich freie Konvektion ausbildet oder nicht. Wegen
ihrer Voraussetzungen (linear, d. h. infinitesimale Ampli-
tuden) kann sie jedoch nicht zur Vorhersage der Größe
von Konvektionsströmungen endlicher Amplitude verwen-
det werden. Hierfür müssen die vollständigen nicht-linearen
gelöst werden, welche die Masse-, Impuls- und Energieer-
haltung in einem zähen kompressiblen oder inkompressiblen
Fluid beschreiben. Eine zweite Grenzwertbetrachtung für
große Rayleigh-Zahlen führt auf die Grenzschichttheorie
(
boundary layer theory
), mit der die Strukturen von Konvek-
tionszellen solcher Strömungen untersucht werden können.
`
Auch die Grenzschichtlösungen lassen sich jedoch vollstän-
dig nur numerisch ermitteln.
Mit einigen Vereinfachungen lässt sich dieses Problem
auf das Problem eines von oben mit T
Rand
beheizten bzw. ge-
kühlten Halbraums zurückführen (vgl. Turcotte & Schubert
horizontale Wärmeleitung gegenüber der Wärmeadvektion
vernachlässigt werden kann, lautet die entsprechende zwei-
dimensionale stationäre Wärmediffusionsgleichung:
œ
z
@
T
@
z
¡
c
p
v
x
@
T
@
@
z
@
x
D
:
(6.109)
Einer konstanten mittleren vertikalen Wärmeleitfähigkeit
entspricht die mittlere thermische Diffusivität
› D œ
z
=.¡
c
p
/
,
und für eine mittlere horizontale Advektionsgeschwin-
digkeit v
x
ergibt sich als charakteristische Transportzeit
im Abschn.
7.11.2
im Anhang beschrieben ist.
Das der stationären Grenzschichttheorie zugrunde lie-
gende Modell besteht aus einer Fluidschicht, deren obere
und untere Randtemperaturen T
o
und T
u
konstant gehalten
schwindigkeit an den Orten des Auf- bzw. Abstroms, also
z. B. bei x
D
0
D
ƒ=2
, verschwindet und bei
x
D ƒ=4
ihren Maximalwert erreicht, wird vereinfachend
von einer konstanten mittleren horizontalen Strömungsge-
schwindigkeit v
x
des an den oberen und unteren Rändern
freien Fluids ausgegangen. Analog wird angenommen, dass
die vertikale Strömungsgeschwindigkeit v
z
an diesen Orten
und x