Geoscience Reference
In-Depth Information
Oft ist es sinnvoll, zunächst die Koeffizienten a
m
und b
m
harmonischen Funktionen mit Hilfe bekannter (Mess-)Werte
der Funktion f
.™; œ/
zu bestimmen:
a
m
.™/
b
m
.™/
cos m
œ
sin m
d
œ
Z
2
1
.1 C •
m
;0
/
D
f
.™; œ/
œ
0
(
1
für m
D 0
mit:
•
m
;0
D
:
(3.125)
0
für m
¤ 0
Integration über
™
liefert dann mit Hilfe bekannter (Mess-)
Werte der Funktion f
.™; œ/
unter Beachtung der Normie-
tionen die Koeffizienten A
m
`
und B
m
`
:
A
m
`
B
m
`
Z
a
m
.™/
b
m
.™/
P
m
.1 C •
m
;0
/
4
D
.2` C 1/
`
.™/
sin
™
d
™
0
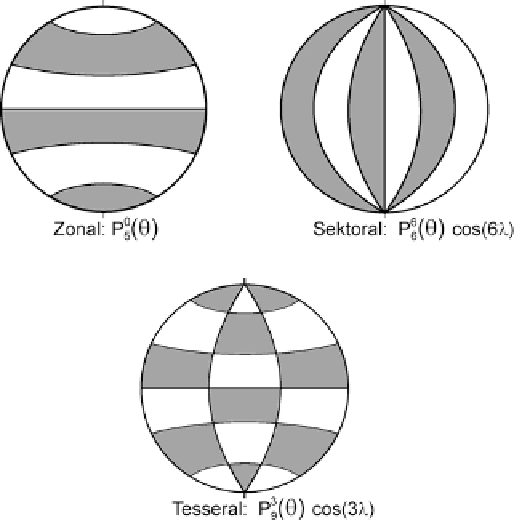
Abb. 3.55
Beispiel der zonalen, sektoralen und tesseralen Kugel-
flächenfunktionen P
0
.™/
,P
6
.™/
cos
.6œ/
und P
9
.™/
cos
.3œ/
Z
a
m
./
b
m
./
P
m
(nach
C
1
.1 C •
m
;0
/
4
D
.2` C 1/
`
./
d
:
(3.126)
1
der eulerschen Formel in eine Reihe komplexer Kugelfunk-
tionen Y
`;
m
und deren Koeffizienten
›
`;
m
entwickelt werden,
wobei f
.™; œ/
eine beliebige komplexe oder reelle Funktion
sein kann:
Die schmidtsche Normierung ist gerade so gewählt, dass
Deshalb skaliert die Größe der Koeffizienten A
m
`
und B
m
`
mit der relativen Energie der jeweiligen Terme. Darum wird
die schmidtsche Normierung üblicherweise insbesondere bei
der Kugelfunktionsentwicklung des Erdmagnetfelds in Ab-
schn.
5.2.3
benutzt.
Unabhängig von der gewählten Normierung verschwin-
den in den normierten Kugelflächenfunktionen Y
m
X
C
X
f
.™; œ/ D
›
`;
m
Y
`;
m
.™; œ/ :
(3.127)
`
D
0
m
D
`
Hierbei sind die Kugelfunktionen und zugeordneten legen-
dreschen Polynome für positives und negatives m wie folgt
definiert:
`
.™; œ/
die Terme P
m
`
.™/
.
œ/
sowie P
m
`
.™/
.
œ/
entlang der
.`
m
/
Breitenkreise, welche den Nullstellen von P
m
cos
m
sin
m
`
.™/
entsprechen. Ebenso verschwinden sie entlang der
.2
m
/
Me-
ridiane von 0-
2
aufgrund der Nullstellen der Sinus- und
se, auf denen die normierten Kugelfunktionen verschwinden,
teilen die Kugeloberfläche in Bereiche unterschiedlichen
Vorzeichens ein. Die sich hieraus ergebenden Muster hän-
gen von den jeweiligen Werten von
`
.™/
e
im
œ
I
Y
`;
m
.™; œ/ D
P
m
Y
`;
m
.™; œ/ D
P
m
.™/
e
im
œ
I
`
m
.`
m
/Š
.` C
m
/Š
P
m
`
.™/
e
im
œ
;
D .1/
mit:
`
m
`:
(3.128)
und m ab: Für m
D 0
variieren die Kugelflächenfunktionen nur mit der Breite und
werden als zonale Harmonische bezeichnet. Für
.`
m
/ D 0
variieren sie nur mit der Länge und werden als sektorale
Harmonische bezeichnet. Wenn sowohl m
`
oberfläche integriert, so ergeben sich unter Berücksichtigung
der Orthogonalitätsbedingung
>0
als auch
.`
m
/>0
ist, bilden sie ein Muster von Vierecken (la-
teinisch:
tesserae
) und werden als tesserale Harmonische
bezeichnet. In allen Fällen wechseln die Kugelfunktionen
das Vorzeichen beim Übergang von einem Bereich in den
anderen.
Z
2
Z
Y
`;
m
.™; œ/
Y
`
0
;
m
0
.™; œ/
d
œ
sin
™
d
™
0
0
4
2` C 1
•
`;`
0
•
m
;
m
0
;
m
D .1/
(3.129)