Geoscience Reference
In-Depth Information
Fig. 1.6.
To the derivation of the radiative transfer equation
volume along the direction of the transfer in (1.33) (i. e. along the direction
normal to the side
dS
). Specify this direction
r
0
and scrutinize radiation scat-
tering from direction
r
with scattering angle
γ
(Fig. 1.6). Encircling the similar
volume around direction
r
(it is denoted as a dashed line), we are obtaining
energy scattered to direction
r
0
. Then employing precedent value of energy
E
0
and definition (1.32), we are obtaining the yield to the emission coefficient
corresponded to direction
r
:
4
γ
Ω
d
λ
dtd
Ω
dl
4
x
(
)
I
(
r
)
dSd
π
ε
=
=
γ
Ω
d
(
r
)
x
(
)
I
(
r
)
d
.
Ω
λ
π
dVd
d
dt
ε
Then it is necessary to integrate value
d
(
r
) over all directions and it leads to
the
integro-differential transfer equation with taking into account the scattering:
I
(
r
0
)+
4
dI
(
r
0
)
dl
=
α
γ
Ω
−
x
(
)
I
(
r
)
d
.
(1.34)
π
π
4
Consider the geometry of solar radiation spreading throughout the atmosphere
for concretization (1.34) as Fig. 1.7 illustrates. As described above in Sect. 1.1we
are presenting the atmosphere as amodel of the plane-parallel and horizontally
homogeneous layer. The direction of the radiation spreading is characterized
with the zenith angle
ϑ
ϕ
counted off an arbitrary
direction at a horizontal plane. Set all coefficients in (1.34) depending on the
altitude (it completely corresponds to reality).
Length element
dl
in the plane-parallel atmosphere is
dl
and with the azimuth
=
|
ϑ
.The
groundsurfaceatthebottomoftheatmosphereisneglectedforthepresent(i.e.
it is accounted that the radiation incoming to the bottom of the atmosphere is
notreflectedbacktotheatmosphereanditisequivalenttothealmostabsorbing
surface). Within this horizontally homogeneous medium, the radiation field is
also the horizontally homogeneous owing to the shift symmetry (the invariance
of all conditions of the problem relatively to any horizontal displacement).
−
dz
cos
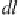





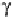

















Search WWH ::

Custom Search