Geoscience Reference
In-Depth Information
conditions and certain conditions of rationality that constitute the basis of the
Expected Utility Theory of von Neumann and Morgenstern (
1944
), the relation of
preference between pairs uniquely determines the distribution of weights desired.
The work of von Neumann and Morgenstern extends that of Daniel Bernoulli, in
the 18th century for the utility of money, and has further extensions designed to
deal with much complex sets than the
finite set of criteria that is the object of
analysis here.
To clarify the hypotheses of von Neumann and Morgenstern is
rst necessary to
formulate precisely the concepts. The necessary concepts are made clear in the next
section. Immediately after, is presented the simple version of the result of von
Neumann and Morgenstern (
1944
) here employed.
2.3.4 Binary Relations
A binary relation on a set C is any subset of the Cartesian product C X C, i.e., any
set of ordered pairs of elements of C. To denote that an ordered pair (c
1
,c
2
)of
elements of C belongs to the binary relation
, we write c
1
c
2
and say that c
1
precedes c
2
.
A binary relation is complete on C if and only if, for all c
1
and c
2
of C, at least
one of the ordered pairs (c
1
,c
2
) and (c
2
,c
1
) belongs to , that means, c
1
c
2
or c
2
c
1
.
A binary relation
i s anti-symmetric if and only if
A binary relation
on C is transitive if and only if,
A binary relation
is an order relation on C if it is anti-symmetric, transitive and
complete on C.
A binary relation is a preference relation on C if it is transitive and complete on C.
So, order relations are preference relations, but these need not be anti-symmetric. For
those criteria for which c
1
c
2
and c
2
c
1
, it will be said that according to the decision
maker is indifferent between c
1
and c
2
and it will be used the notation c
1
*
c
2
.
A distribution of weights on a set C is any positive function u with domain C,
i.e., any subset of the Cartesian product CXR
+
such that for every element x of C
there is a unique positive number y for which x
ð Þ2
u is
usually employed the notation y = u(x) or is said that y is the weight of x, the
preference value of x or the utility of x. To simplify the arguments, is usually
assumed that u is a probability.
The von Neumann and Morgenstern theory involves extending the preference
relations on C to preference relations on the set D(C) of distributions of weights on
C. Let us denote by
ð
;
y
Þ2
u
:
Instead of x
;
y
the extension of
to D(C). For the theorem to hold, these















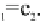


























Search WWH ::

Custom Search