Geoscience Reference
In-Depth Information
solution may be observed may be small. For a bifurcation
diagram see
Guckenheimer and Holmes
[1983], where an
example of a situation in which a stable 3-torus exists is
also given. Also, see
Kuznetsov
[2004] in which this case
corresponds to difficult case 6.
Case VIa is observed at low Prandtl number, in partic-
ular, at the Prandtl number of mercury for the
(m
1
,
m
2
)
=
(
5,4
)
and
(
3,2
)
mode interaction points and near this for
the third point. These results are not inconsistent with the
experimental results of
Fein and Pfeffer
[1976], although
they do not explain some key experimental observations,
in particular, the absence of the upper symmetric regime.
In the current analysis, the primary transition occurs very
near to the experimentally observed transition from non-
geostrophic turbulence to the regular wave regime, which
suggests that the observed turbulence may be related to
this bifurcation. In particular, case VIa predicts the occur-
rence of 3-frequency flow, near which chaotic motion may
be found.
Preceding the appearance of case VIa, for all mode
interaction points, is case VIb. However, for intermediate
values of the Prandtl number, we observe some differences
in the dynamics for the different mode interaction points.
The remaining cases that may be observed are discussed
below.
In Cases Ib, II, and III
1
, the analysis can say little about
the flow that may be observed. In particular, no stable peri-
odic or mixed-mode solution in any region of parameter
space is predicted. See
Guckenheimer and Holmes
[1983]
for the bifurcation diagram with corresponding phase por-
traits of case Ib. In all these cases, both Hopf bifurcations
are subcritical, and therefore without the computation of
higher order coefficients, it is not possible to determine the
dynamics that would be observed. The mixed-mode solu-
tion corresponding to fixed point 4 is also unstable and
thus would not be physically observable near these bifur-
cation points, although characteristics of the solution may
be observed in transient flows.
In cases V, VIIb, and VIb,
2
we have
a
=+1and
d
=
μ
2
ρ
2
μ
2
=
c
μ
1
ρ
1
μ
1
μ
2
=(
c
-
1
)/(
b
+
1
)μ
1
μ
2
=-
μ
1/
b
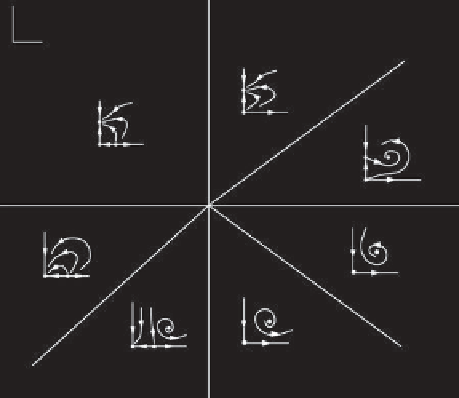
Figure 2.8.
Two-dimensional bifurcation diagram for case VIIa,
subcase (b). See caption of Figure 2.5 for description.
The fixed point 4 of case VIIa, subcase (b) exists in the
wedge defined by
μ
2
<
μ
1
/b
and
μ
2
< cμ
1
,where
the borders of the wedge, given by
μ
2
=
−
μ
1
/b
and
μ
2
=
cμ
1
, are in the lower left quadrant and upper right
quadrant, respectively, of the parameter space. A linear
stability analysis reveals that the eigenvalues of fixed point
4 are a complex conjugate pair with real parts positive
for
μ
2
<(c
−
1
)/(b
+1
)μ
1
and with real parts nega-
tive for
μ
2
>(c
−
1
)/(b
+1
)μ
1
, i.e.; fixed point 4 is a
stable focus in the later case. Thus, there is a stable mixed-
mode solution in the wedge defined by
μ
2
< cμ
1
and
μ
2
>(c
−
1
)/(b
+1
)μ
1
. The phase portraits in all regions
of the space of parameters are presented in Figure 2.8.
Along the curve
μ
2
=
(c
−
1
)/(b
+1
)μ
1
, a Hopf bifur-
cation of fixed point 4 occurs. This would imply that there
is a periodic orbit for the reduced system (2.16)-(2.17)
near this line. In the full normal form equations (2.16)-
(2.19), this bifurcation corresponds to a bifurcation from
the 2-torus, and the periodic orbit of the reduced system
would correspond to a 3-torus. In general, the correspond-
ing flow that would be observed in the annulus would have
three non-rationally-related frequencies. The stability of
this solution (i.e., whether the bifurcation is subcritical or
supercritical) would depend on the fifth-order terms in
the normal form equations. These would be formidable
to compute in this context, and so we do not attempt it
here. It would be interesting to see if evidence of such a
solution could be seen in either experiment or numerical
simulation.
Similarly, in case VIa, a Hopf bifurcation of fixed point
4 occurs, and again, depending on the higher order terms,
it may be possible to observe a three-frequency flow. In
this case, however, the wedge in which the mixed-mode
−
1,
i.e., a subcritical Hopf bifurcation occurs at
μ
1
= 0 while
a supercritical Hopf occurs at
μ
2
= 0. Thus, we would
expect to observe a stable rotating wave of wave number
m
2
as parameters are varied across
μ
2
=0suchthat
μ
1
<
0.
However, all other solutions are unstable, and therefore,
the analysis cannot determine the dynamics that will be
observed in other regions. For example, for case V, the
two-parameter bifurcation diagram with corresponding
phase portraits for all regions of the space of parameters is
−
1
These cases correspond to the time reverse of simple case 1, the time
reverse of simple case 2, and the time reverse, with index switch, of
simple case 3, respectively, of
Kuznetsov
[2004].
2
These cases correspond to the time reverse, with index switch, of
difficult case 4, difficult case 3, and difficult case 5, respectively„ of
Kuznetsov
[2004].